Nguồn: wcipeg

Biên soạn:

Nguyễn Châu Khanh - VNU University of Engineering and Technology (VNU-UET)
Bùi Minh Hoạt - VNU University of Engineering and Technology (VNU-UET)

Reviewer:

Hoàng Xuân Nhật

Mở đầu

Bài viết này sẽ giúp bạn tìm hiểu về bài toán sắp xếp Tô-pô (Topological Sort). Sắp xếp Tô-pô là một trong những bài toán có tính ứng dụng cao trong Tin học lẫn Toán học và cả trong đời sống.

Bài toán sắp xếp Tô-pô

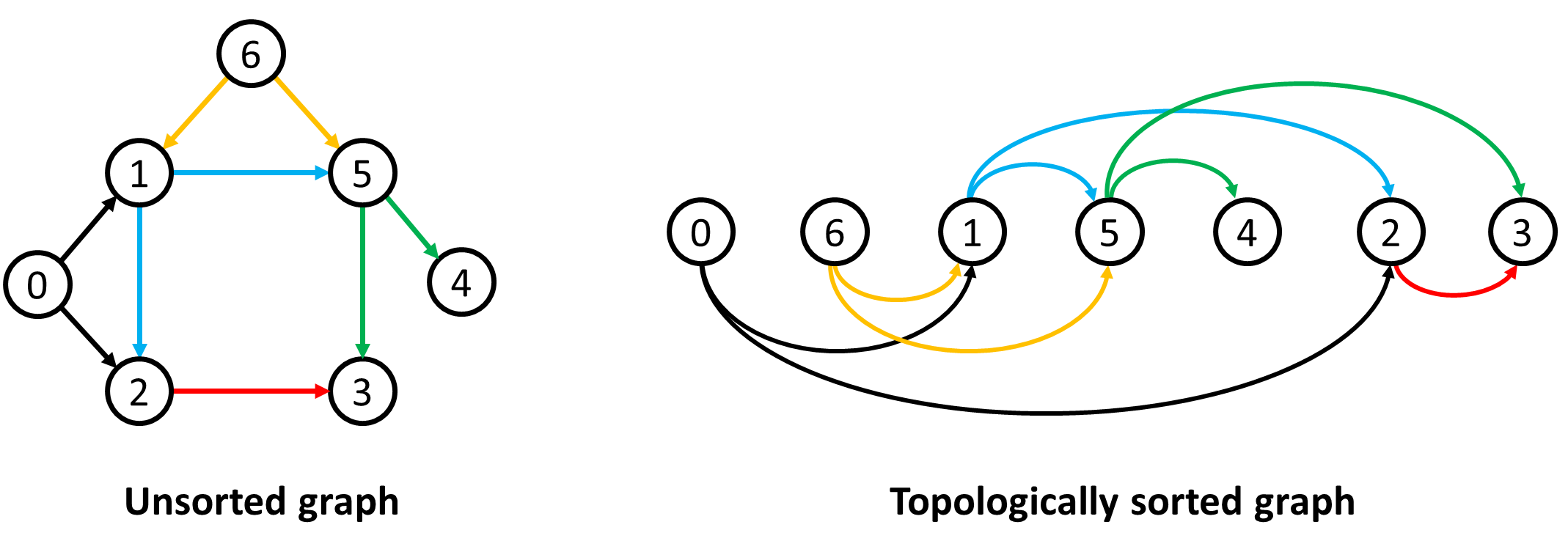
Thứ tự Tô-pô của một đồ thị có hướng là một thứ tự sắp xếp của các đỉnh sao cho với mọi cung từ đỉnh $u$ đến đỉnh $v$ trong đồ thị, $u$ luôn nằm trước $v$.
Bài toán xác định thứ tự Tô-pô gọi là Bài toán sắp xếp Tô-pô.

Cảm hứng

Sắp xếp Tô-pô được áp dụng nhiều nhất đối với các bài toán biểu diễn mối quan hệ phụ thuộc giữa các đối tượng.
Ví dụ như nó có thể được áp dụng trong việc lập ra lịch trình công việc. Một tập hợp các công việc phụ thuộc lẫn nhau có thể được sắp xếp theo một thứ tự nhất định để chúng được thực hiện.
Ta có ví dụ thực tế như sau:
- Để có được bằng cấp, sinh viên phải hoàn thành một số khóa học bắt buộc. Các khóa học này không nhất thiết phải được hoàn thành theo bất kỳ trình tự nhất định nào, nhưng có một số khóa học là điều kiện tiên quyết cho những khóa học khác.
- Ví dụ, khóa học "Giới thiệu về thuật toán trong Tin học" có thể phụ thuộc vào các khóa học “Nhập môn thuật toán”, “Giới thiệu về cấu trúc dữ liệu”, “Nhập môn lập trình”, … Đây là mối quan hệ phụ thuộc; việc tham gia các khóa học sau phụ thuộc vào việc tham gia các khóa học tiên quyết của nó.
- Từ đó, ta có thể xây dựng một đồ thị với mỗi đỉnh tương ứng với một khóa học và mỗi cạnh có hướng từ đỉnh $u$ đến đỉnh $v$ khi và chỉ khi khóa học tương ứng với đỉnh $u$ là điều kiện tiên quyết cho khóa học tương ứng với đỉnh $v$. Việc sắp xếp thứ tự các đỉnh của đồ thị này sẽ cung cấp một thứ tự khả thi mà các khóa học có thể được thực hiện.
- Tất nhiên, nó không thể được sử dụng để giải quyết vấn đề nghiêm trọng hơn về xung đột lịch trình.

Điều kiện tồn tại thứ tự Tô-pô

Dễ nhận thấy rằng, một đồ thị tồn tại thứ tự Tô-pô thì đồ thị đó phải là đồ thị có hướng và không có chu trình (Directed Acyclic Graph - DAG). Vì nếu đồ thị có chứa một chu trình, $v_1 v_2 … v_n v_1$ thì $v_2$ phải đứng sau $v_1$ theo thứ tự Tô-pô, $v_3$ phải đứng sau $v_2$, v.v…; nhưng sau đó $v_1$ phải đứng sau $v_1$, dẫn đến kết luận vô lý khi $v_1$ phải đứng sau chính nó trong danh sách.
Vậy câu hỏi đặt ra là liệu điều kiện này có đủ hay không? Có đúng là một đồ thị có thể được sắp xếp theo thứ tự Tô-pô khi và chỉ khi đồ thị đó là một $DAG$ ? Câu trả lời là đúng.
Định lý : Một đồ thị tồn tại thứ tự Tô-pô khi và chỉ khi đồ thị đó là DAG. Đồng nghĩa, mọi DAG đều luôn tồn tại ít nhất một thứ tự Tô-pô, và có thuật toán để tìm thứ tự Tô-pô trong thời gian tuyến tính.
Chứng minh :
- Rõ ràng, một $DAG$ chỉ gồm $1$ đỉnh duy nhất luôn có thể được sắp xếp theo thứ tự Tô-pô. Khi đó, danh sách Tô-pô trong trường hợp này chỉ bao gồm chính đỉnh đó.
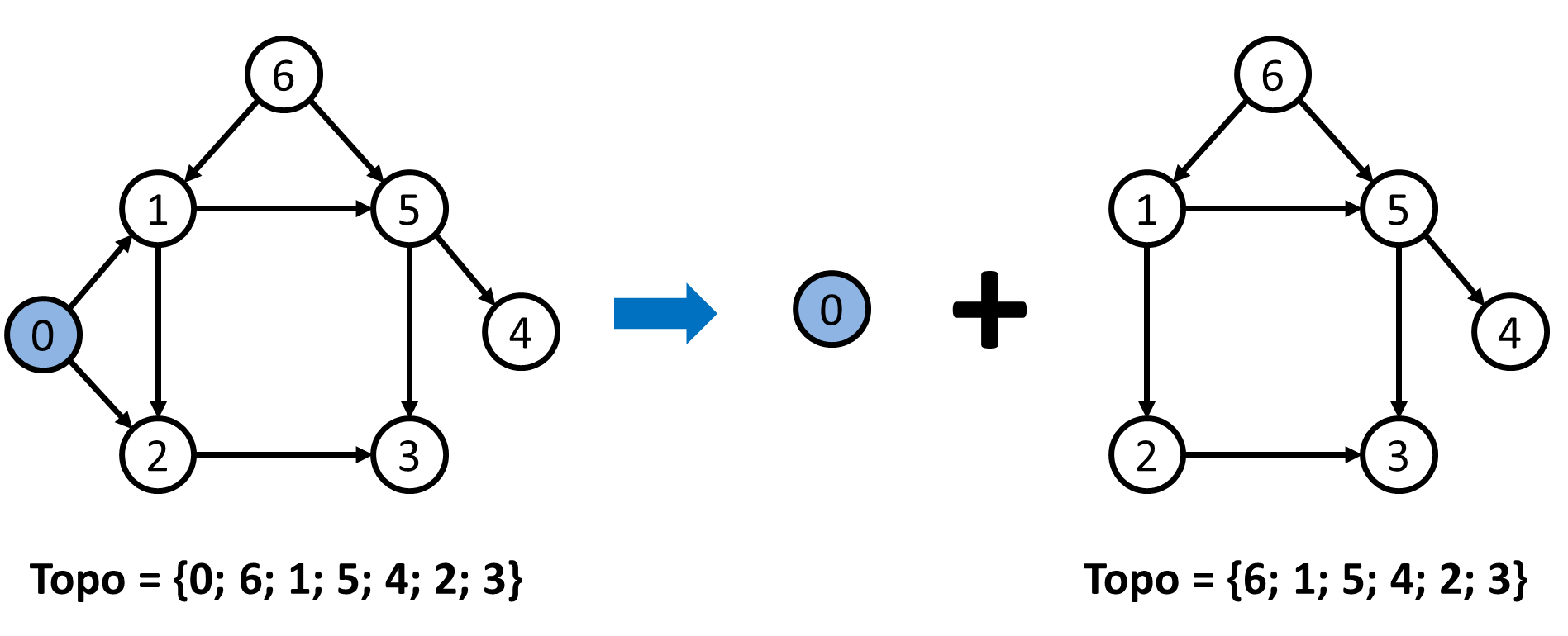
- Giả sử rằng bất kỳ $DAG$ nào có $n$ đỉnh đều có thể được sắp xếp theo thứ tự Tô-pô. Bây giờ hãy xem xét các $DAG$ có $n+1$ đỉnh. Nhớ lại rằng mọi $DAG$ đều có ít nhất một đỉnh nguồn (đỉnh không có cung vào). Hãy để đỉnh nguồn này làm giá trị đầu tiên trong danh sách Tô-pô, rồi loại bỏ đỉnh này cùng cách cạnh kề với nó ra khỏi đồ thị. Khi đó, ta sẽ có được đồ thị mới gồm $n$ đỉnh là đồ thị con của đồ thị ban đầu. Rõ ràng, các chu trình không thể được tạo ra bằng cách loại bỏ các cạnh và đỉnh. Bằng giả thiết ban đầu, ta có thể sắp xếp đồ thị con này theo thứ tự Tô-pô. Sau đó, ta nối thứ tự Tô-pô của đồ thị con vào cuối danh sách hiện tại để có được danh sách thứ tự Tô-pô của đồ thị $n+1$ đỉnh với đỉnh nguồn là giá trị đầu tiên trong danh sách.
- Ví dụ minh họa: Để xác định thứ tự Tô-pô của $DAG$ gồm $7$ đỉnh, ta thêm đỉnh nguồn $0$ vào trong danh sách Tô-pô rồi nối thêm thứ tự Tô-pô của đồ thị con $6$ đỉnh.
- Bây giờ, với hai đỉnh bất kỳ $u$ và $v$ trong danh sách Tô-pô, giả sử $u$ đứng trước $v$:
  - Nếu $u$ là giá trị đầu tiên trong danh sách (đỉnh nguồn), trong trường hợp đó, rõ ràng là không thể tồn tại cạnh nối từ $v \rightarrow u$.
  - Nếu cả hai đỉnh $u$ và $v$ đều không phải là giá trị đầu tiên trong danh sách, dù trong trường hợp nào thì chúng đều được sắp xếp đúng vì chúng thuộc phần đồ thị con được sắp xếp theo thứ tự Tô-pô.
- Do đó, danh sách $n+1$ đỉnh mới này là một thứ tự Tô-pô của $DAG$ gồm $n+1$ đỉnh.
Tính chất
- Thứ tự Tô-pô không nhất thiết phải là duy nhất. Có thể có một số thứ tự Tô-pô khác nhau trong một đồ thị.
- Tuy nhiên, thứ tự Tô-pô sẽ là duy nhất khi $DAG$ có đường đi $Hamilton$.

Bài toán 1 - Sắp xếp TOPO

TOPOSORT – Sắp xếp TOPO

Đề bài

Cho đồ thị có hướng không chu trình (Directed Acyclic Graph - DAG) $G(V, E)$. Hãy đánh số lại các đỉnh của $G$ sao cho chỉ có cung nối từ đỉnh có chỉ số nhỏ đến đỉnh có chỉ số lớn hơn.

Input

Dòng đầu chứa hai số nguyên $n$ và $m$ là số đỉnh và số cung của đồ thị $G$;
$m$ dòng tiếp theo, mỗi dòng chứa một cặp số $u, v$ cho biết một cung nối từ $u$ tới $v$ trong $G$.

Output

Ghi ra $n$ số nguyên dương, số thứ $i$ là chỉ số của đỉnh thứ $i$ sau khi đánh số lại. Hai số trên cùng một dòng được ghi cách nhau một dấu cách.

Constraints

$1 \le n \le 100;$ $0 \le m \le \frac{n(n-1)}{2}$.

Example

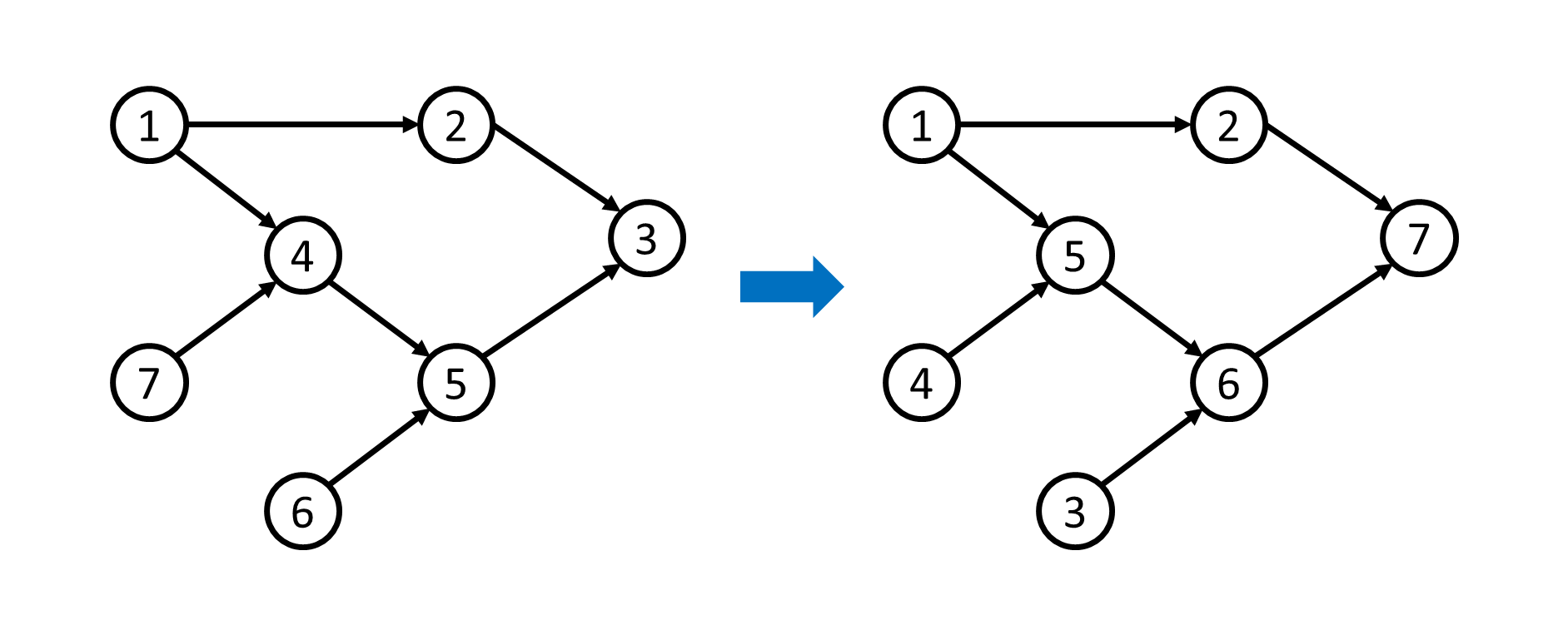
Input

Output

1 2 7 5 6 3 4

Note

Thuật toán 1

Từ phần chứng minh của định lý trên (trong mục Điều kiện tồn tại thứ tự Tô-pô), ta có thuật toán để tìm ra một thứ tự Tô-pô như sau:
1. Bắt đầu với một danh sách Tô-pô trống.
2. Tìm đỉnh nguồn của $DAG$. Thêm đỉnh này vào cuối danh sách Tô-pô.
3. Loại bỏ đỉnh này và tất cả các cạnh kề với nó ra khỏi $DAG$.
4. Nếu số đỉnh của $DAG$ lớn hơn $0$, hãy quay lại bước $2$.
Sau khi kết thúc, danh sách sẽ chứa một thứ tự Tô-pô của $DAG$.
Để thực hiện thuật toán này một cách hiệu quả, ta sẽ không thực sự loại bỏ các đỉnh khỏi đồ thị trong bước $3$, vì đây là một quá trình phức tạp nếu đồ thị được biểu diễn dưới dạng ma trận kề hoặc danh sách kề.
Ta cũng sẽ không duyệt qua toàn bộ đồ thị ở mỗi bước $2$ để tìm đỉnh nguồn. Điều này cũng tốn kém về mặt thời gian và tính toán.
Thay vào đó, ta có những nhận xét sau:
- Một đỉnh là đỉnh nguồn khi và chỉ khi số lượng cung vào của nó bằng $0$.
- Nếu một đỉnh không phải là đỉnh nguồn, nó sẽ trở thành đỉnh nguồn sau khi tất cả các cung vào của nó đã bị xóa. Một cung vào của nó chỉ bị xóa khi đỉnh còn lại của cung đó bị xóa.
- Giả sử ta biết vị trí của tất cả các đỉnh nguồn trong $DAG$ và ta thực hiện các bước $2$ và $3$ một lần. Sau đó, những đỉnh duy nhất có thể trở thành đỉnh nguồn là những đỉnh có cung vào nối với đỉnh vừa bị xóa.
Sau khi xác định được thứ tự Tô-pô của đồ thị, ta sẽ đánh số lại các đỉnh của đồ thị theo thứ tự.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 110 .
Mảng ans[] - Mảng đánh số lại các đỉnh.
Mảng indegree[] - Lưu số lượng cung vào của mỗi đỉnh.
Vector g[] - Danh sách cạnh kề của mỗi đỉnh.
Vector topo - Danh sách thứ tự Tô-pô.
Queue listSource - Danh sách các đỉnh không có cung vào.

#include <bits/stdc++.h>

using namespace std;

const int maxN = 110;

int n, m;
int indegree[maxN], ans[maxN];
vector <int> g[maxN], topo;
queue <int> listSource;

main() {
    cin >> n >> m;
    while (m--) {
    	int u, v;
    	cin >> u >> v;
    	g[u].push_back(v);
    	indegree[v]++;
    }

    for (int u = 1; u <= n; ++u)
    	if (!indegree[u]) listSource.push(u);

    while (!listSource.empty()) {
    	int u = listSource.front();
    	listSource.pop();
    	topo.push_back(u);
    	for (auto v : g[u]) {
    		indegree[v]--;
    		if (!indegree[v]) listSource.push(v);
    	}
    }

    if (topo.size() < n) {
    	cout << "Error: graph contains a cycle";
    	return 0;
    }
    
    /* Sau khi xác định được thứ tự Tô-pô của đồ thị, ta sử dụng
       mảng ans để đánh số lại các đỉnh */
    int cnt = 0;
    for (auto x : topo) ans[x] = ++cnt;
    	
    for (int i = 1; i <= n; ++i) cout << ans[i] << ' ';
}

Mô tả quá trình

Thứ tự Tô-pô không phải là duy nhất. Quá trình sau chỉ mô tả lại quá trình xác định $1$ thứ tự Tô-pô theo như code mẫu.

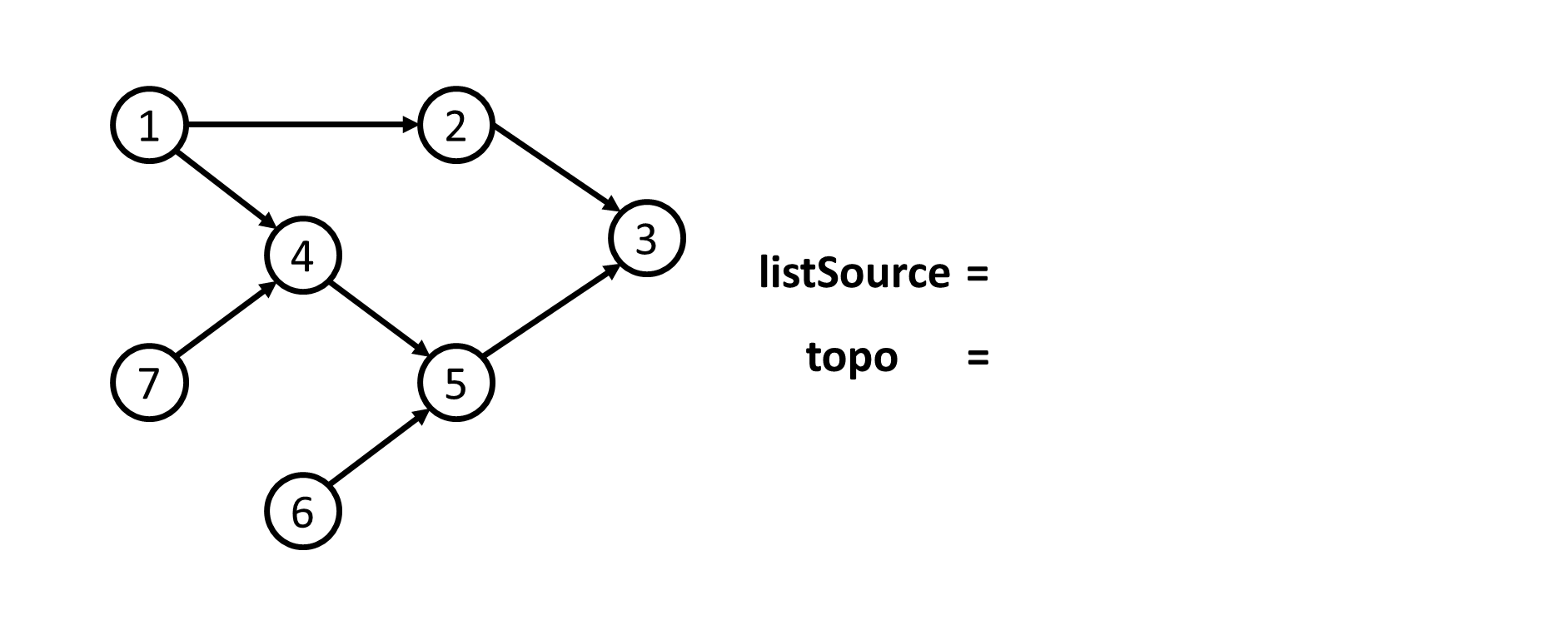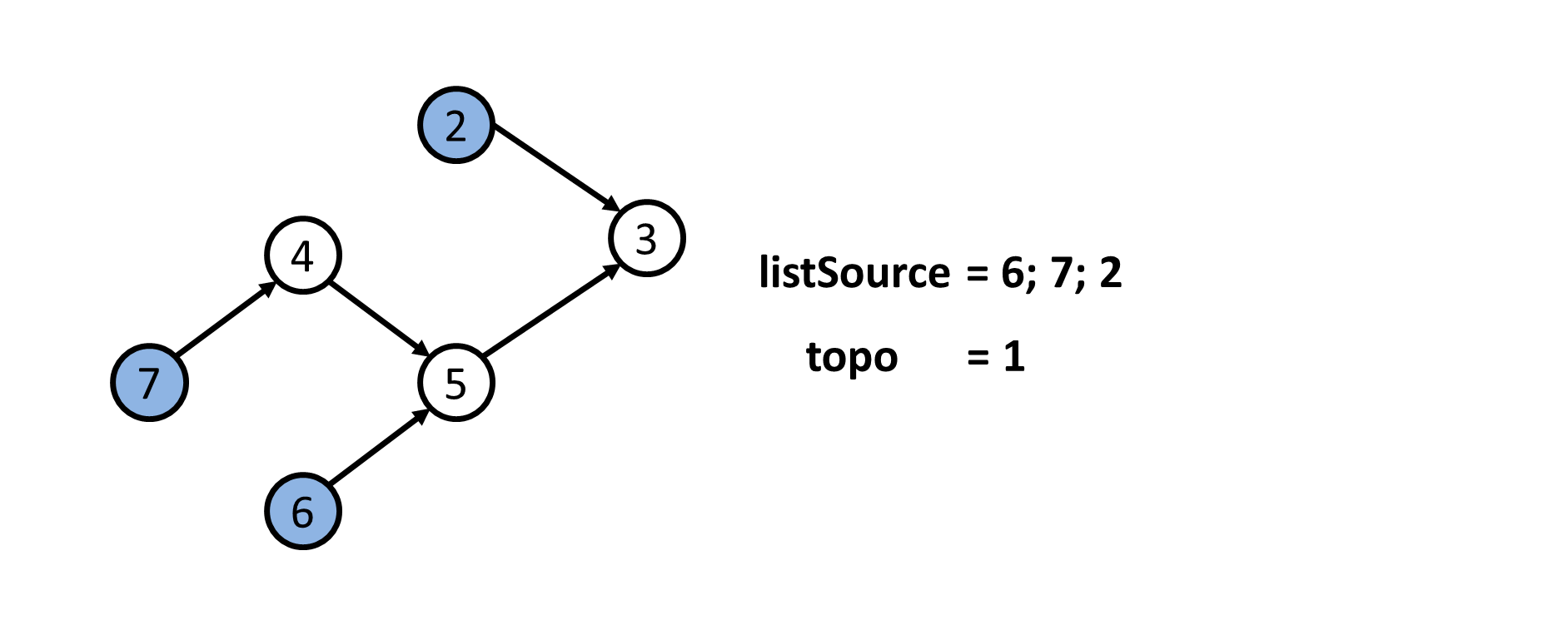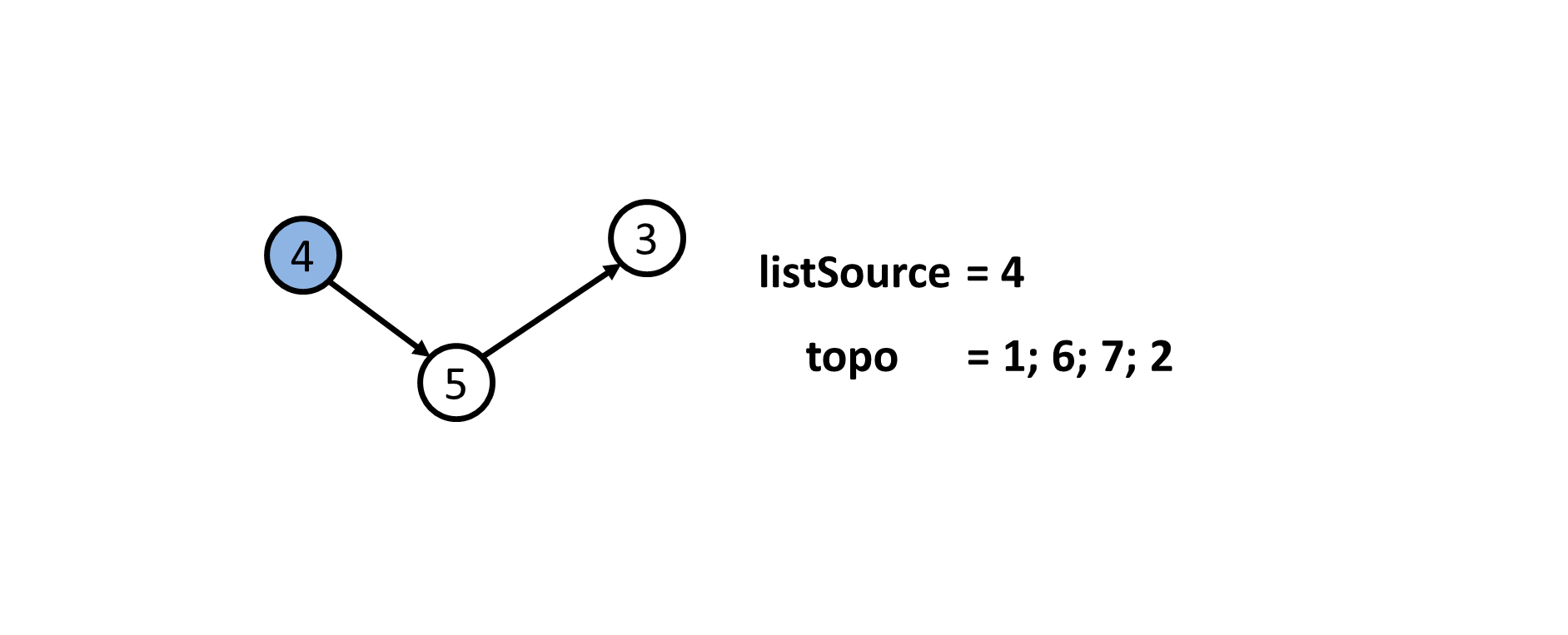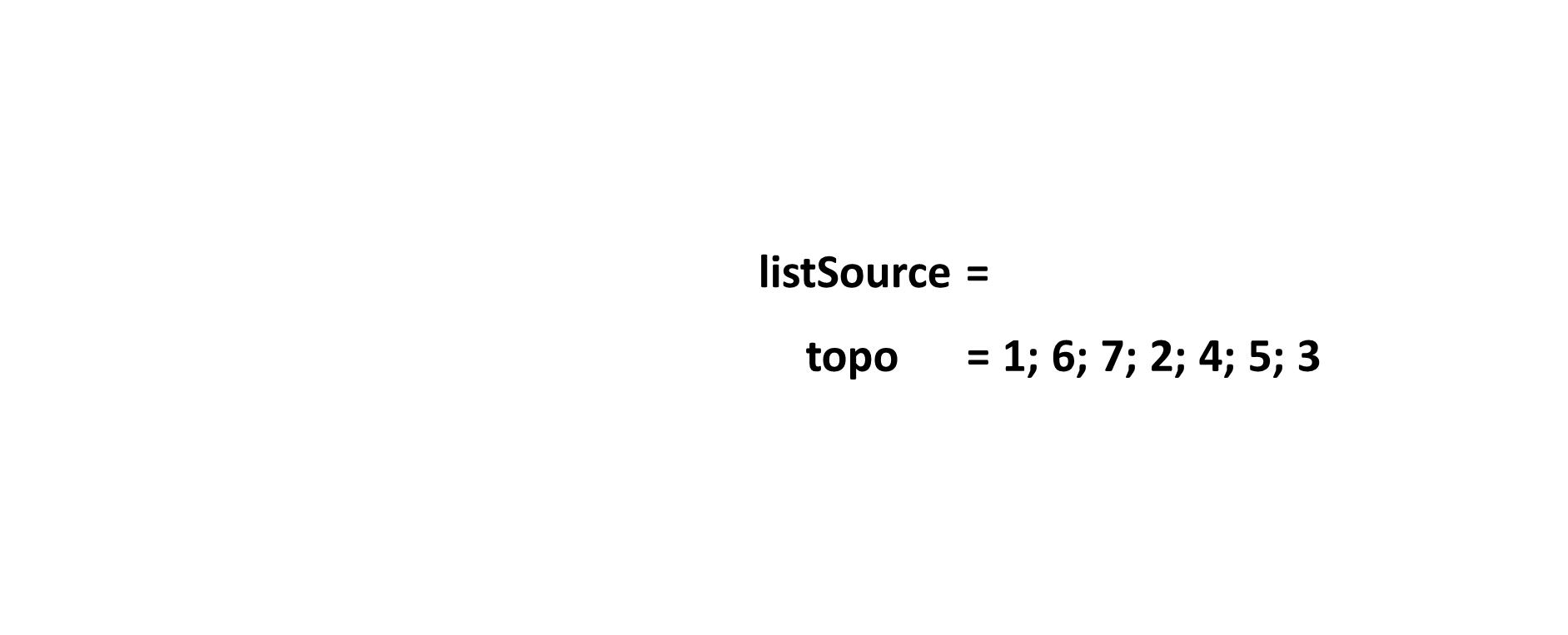
Sau khi xác định được thứ tự Tô-pô của đồ thị là topo = {1; 6; 7; 2; 4; 5; 3}. Ta đánh số lại các đỉnh. Khi đó ta sẽ có mảng ans = {1; 4; 7; 5; 6; 2; 3}.

Đánh giá

Để thực hiện thuật toán này một cách hiệu quả, ta cần phải có khả năng duyệt qua các đỉnh kề của một đỉnh một cách hiệu quả. Điều này được thực hiện tốt nhất bằng cách sử dụng danh sách kề (vector g[]).
Ngoài ra, listSource nên là một ngăn xếp (stack) hoặc một hàng đợi (queue) để việc thêm và loại bỏ các phần tử có thể được thực hiện trong thời gian không đổi.
Thuật toán sẽ luôn tìm ra một thứ tự Tô-pô nếu nó tồn tại. Còn nếu nó không tồn tại (nghĩa là đồ thị ban đầu không phải là $DAG$ ) thì danh sách topo sẽ không được điền đầy đủ và thông báo lỗi sẽ được in ra.
Thứ tự Tô-pô sẽ là duy nhất khi và chỉ khi listSource chứa chính xác một đỉnh ở đầu mỗi lần lặp của vòng lặp while.

Độ phức tạp

Ở vòng lặp while để duyệt các đỉnh trong listSource, ta mất độ phức tạp $O(n)$ vì mỗi đỉnh chỉ được thêm vào nhiều nhất $1$ lần (ở ban đầu hoặc ngay sau khi cạnh vào cuối cùng của nó bị loại bỏ). Và ta sẽ mất thêm độ phức tạp $O(m)$ để duyệt các cạnh vì mỗi cạnh chỉ được kiểm tra nhiều nhất $1$ lần trong vòng lặp while (khi đỉnh nối với nó được lấy ra).
Nhìn chung, độ phức tạp của thuật toán này là $O(n+m)$.

Thuật toán 2

Có một thuật toán khác cho sắp xếp Tô-pô dựa trên tìm kiếm theo chiều sâu (Depth-First Search - DFS).
Đối với thuật toán 2, quá trình tìm kiếm theo chiều sâu sẽ trả ra danh sách nghịch đảo thứ tự Tô-pô. Đơn giản hơn, nó chính là danh sách Tô-pô bị đảo ngược lại.
Điều này tương đương với việc nếu tồn tại cung $u \rightarrow v$ thì $u$ có số thứ tự cao hơn $v$ trong danh sách nghịch đảo Tô-pô.
Ví dụ minh họa:
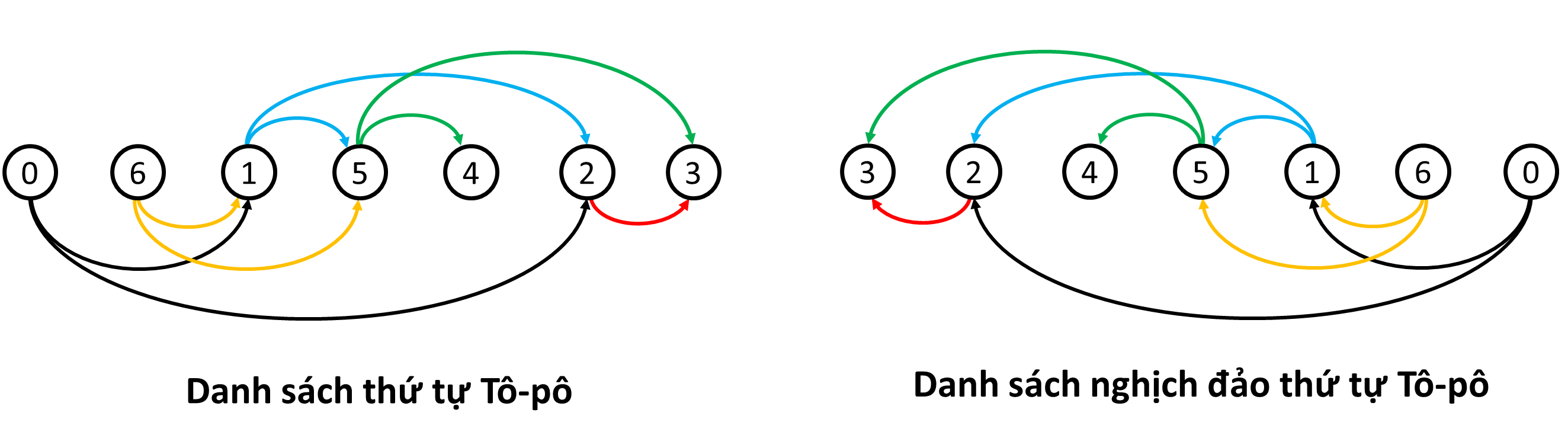
Chứng minh: Hãy xem xét cây DFS của đồ thị (tìm hiểu thêm về cây $DFS$ tại đây):
- Nếu $u$ là tổ tiên của $v$ trong cây $DFS$, thì quá trình duyệt xong cây con gốc $v$ sẽ kết thúc sớm hơn quá trình duyệt xong cây con gốc $u$. Do đó, $u$ sẽ có số thứ tự cao hơn $v$ trong danh sách.
- Nếu $u$ là tổ tiên của $v$ trong cây $DFS$ và tồn tại cung nối từ $1$ đỉnh thuộc cây con gốc $v$ đến đỉnh $u$ thì đồ thị có chu trình (không phải là DAG) nên sẽ không tồn tại thứ tự Tô-pô.
- Nếu $u$ không phải là tổ tiên của $v$ và $v$ cũng không phải là tổ tiên của $u$ trong cây $DFS$ thì khi đó, $2$ đỉnh $u$ và $v$ sẽ nằm trên $2$ nhánh khác nhau của cây $DFS$. Do đó cung nối từ nhánh chứa đỉnh $u$ đến nhánh chứa đỉnh $v$ là cung chéo và đỉnh $u$ sẽ được duyệt sau $v$ nên sẽ có số thứ tự cao hơn $v$ trong danh sách.
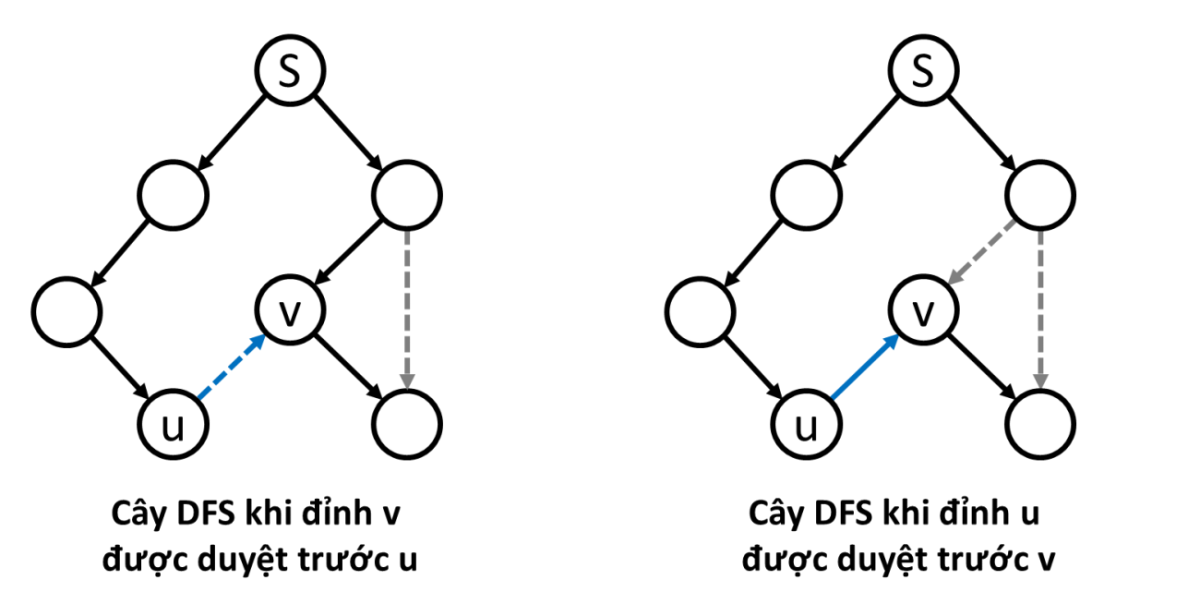
  - Ví dụ minh họa: Bắt đầu duyệt $DFS$ từ đỉnh $S$. Các "cạnh nét liền" là cung của cây $DFS$. Các "cạnh nét đứt" không phải là cung của cây $DFS$. Với cung chéo $u \rightarrow v$, đỉnh $v$ chắc chắn sẽ được duyệt trước $u$. Vì nếu $u$ được duyệt trước $v$ thì đỉnh $u$ sẽ là tổ tiên của đỉnh $v$ và cung $u \rightarrow v$ sẽ không còn là cung chéo nữa, khi đó ta xét giống như ở trường hợp đầu tiên.
Từ những nhận xét trên, ta có thuật toán để tìm ra một thứ tự Tô-pô như sau:
- Xuất phát từ một điểm chưa được duyệt, ta bắt đầu duyệt $DFS$ trên đồ thị xuất phát từ điểm đó.
- Dùng một mảng để lưu trạng thái của mỗi đỉnh. Có $3$ trạng thái:
  - Trạng thái 0 : Đỉnh chưa được duyệt (chưa từng được gọi hàm $DFS$).
  - Trạng thái 1 : Đỉnh vẫn đang duyệt (hàm $DFS$ với đỉnh này chưa kết thúc).
  - Trạng thái 2 : Đỉnh đã duyệt xong (hàm $DFS$ với đỉnh này đã kết thúc).
- Hiển nhiên, khi đang duyệt mà ta gặp phải một đỉnh ở trạng thái 1 thì điều đó chứng tỏ đồ thị đang xét có chứa chu trình, và không thể sắp xếp Tô-pô được.
- Sau khi kết thúc duyệt $DFS$ trên đồ thị, thứ tự hoàn tất duyệt của mỗi đỉnh chính là danh sách nghịch đảo thứ tự Tô-pô.
- Để có được thứ tự Tô-pô, đơn giản ta chỉ cần đảo ngược lại danh sách nghịch đảo thứ tự Tô-pô.
Sau khi xác định được thứ tự Tô-pô của đồ thị, ta sẽ đánh số lại các đỉnh của đồ thị theo thứ tự.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 110 .
Mảng ans[] - Mảng đánh số lại các đỉnh.
Mảng visit[] - Mảng lưu trạng thái của mỗi đỉnh.
Vector g[] - Danh sách cạnh kề của mỗi đỉnh.
Stack topo - Danh sách thứ tự Tô-pô.

#include <bits/stdc++.h>

using namespace std;

const int maxN = 110;

int n, m;
int visit[maxN], ans[maxN];
vector <int> g[maxN];
stack <int> topo;

void dfs(int u) {
    visit[u] = 1;
    for (auto v : g[u]) {
        if (visit[v] == 1) {
            cout << "Error: graph contains a cycle";
            exit(0);
        }
        if (!visit[v]) dfs(v);
    }
    topo.push(u);
    visit[u] = 2;
}

main() {
    cin >> n >> m;
    while (m--) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
    }
    for (int i = 1; i <= n; ++i)
        if (!visit[i]) dfs(i);

    /* Sau khi xác định được thứ tự Tô-pô của đồ thị, ta sử dụng
       mảng ans để đánh số lại các đỉnh */
    int cnt = 0;
    while (!topo.empty()) {
        ans[topo.top()] = ++cnt; 
        topo.pop();
    }

    for (int i = 1; i <= n; ++i) cout << ans[i] << ' ';
}

Mô tả quá trình

Thứ tự Tô-pô không phải là duy nhất. Quá trình sau chỉ mô tả lại quá trình xác định $1$ thứ tự Tô-pô theo như code mẫu.

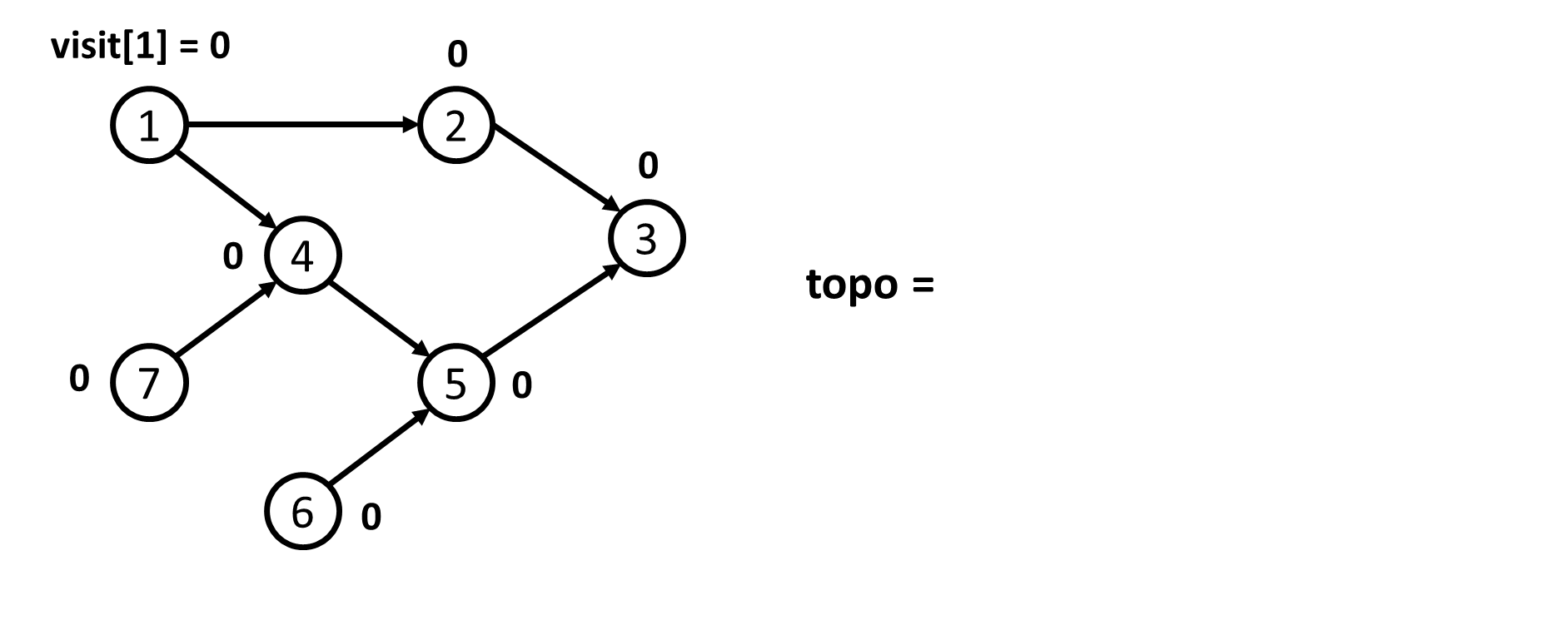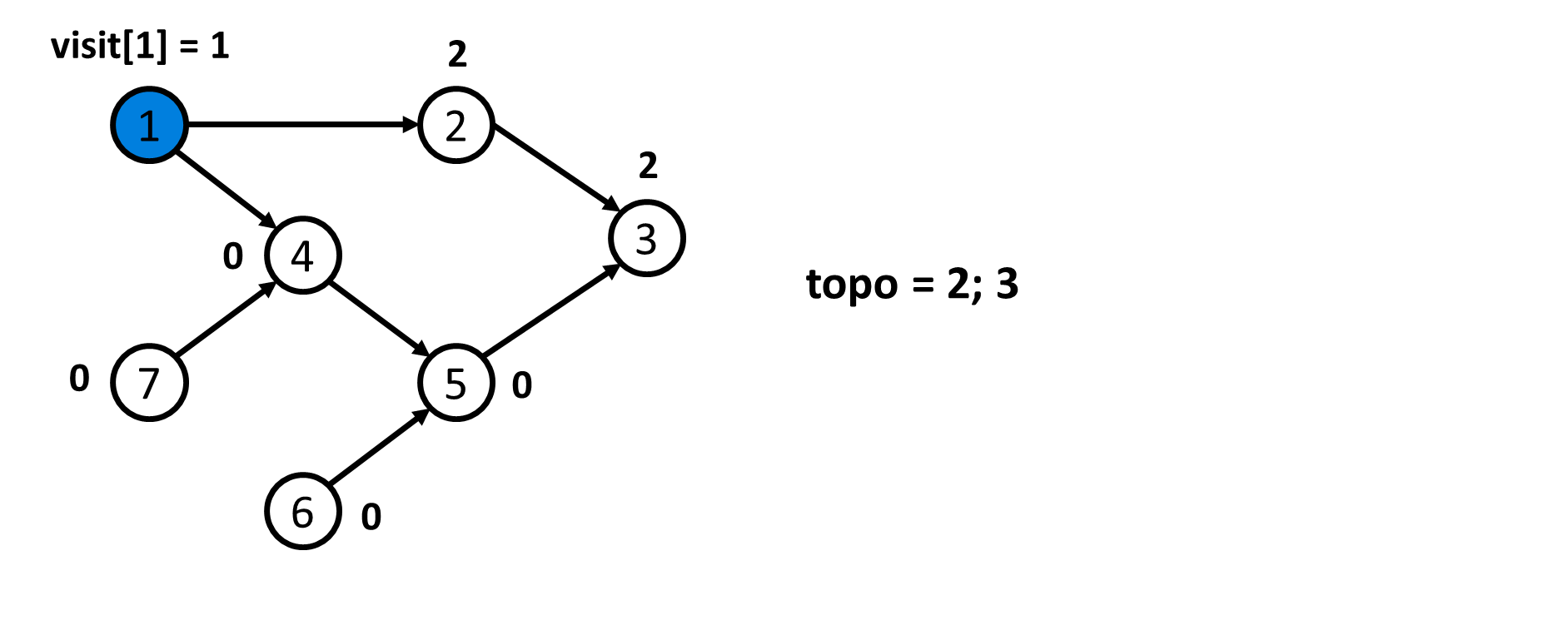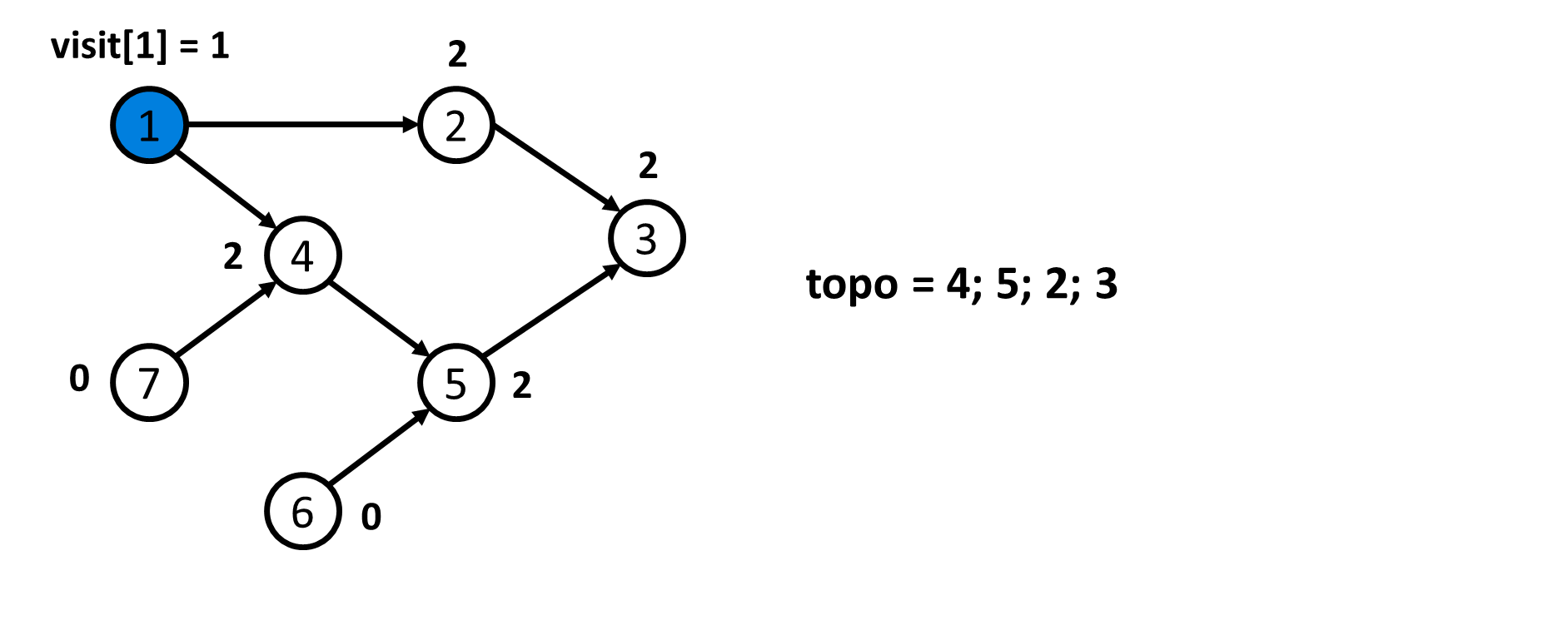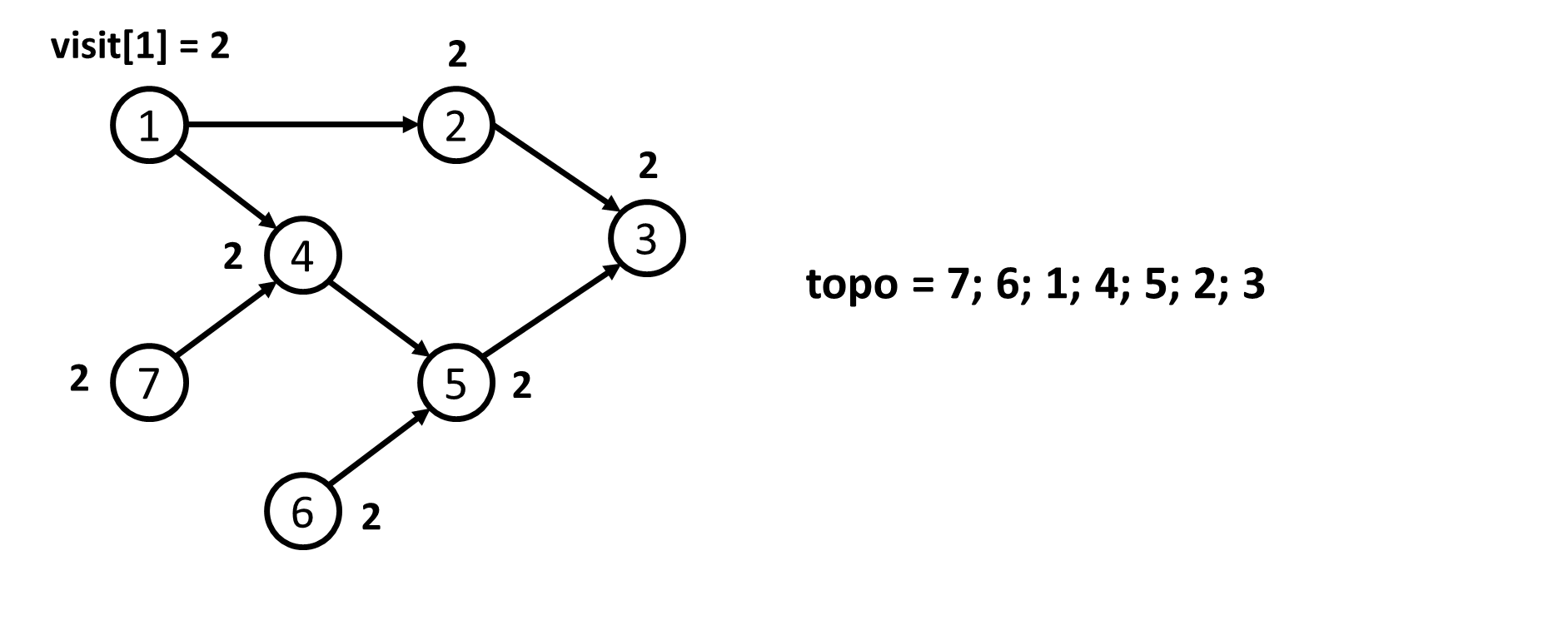
Sau khi xác định được thứ tự Tô-pô của đồ thị là topo = {7; 6; 1; 4; 5; 2; 3}. Ta đánh số lại các đỉnh. Khi đó ta sẽ có mảng ans = {3; 6; 7; 4; 5; 2; 1}.

Đánh giá

Thuật toán 2 đơn giản và dễ cài đặt so với hơn thuật toán 1.
Ta sử dụng ngăn xếp (stack) để có thể dễ dàng đảo ngược lại thứ tự hoàn tất duyệt của mỗi đỉnh. Nói cách khác là ta đảo ngược lại danh sách nghịch đảo thứ tự Tô-pô để có được thứ tự Tô-pô.
Với phương pháp sắp xếp Tô-pô bằng $DFS$, nếu đồ thị không phải là $DAG$ thì ta vẫn có thể tìm ra một thứ tự, nhưng ta lại có thế dùng $DFS$ để kiểm tra luôn xem đồ thị có là $DAG$ hay không.
Nếu đồ thị không phải là $DAG$ thì thông báo lỗi sẽ được in ra.

Độ phức tạp

Ở hàm $DFS$, ta mất độ phức tạp $O(n)$ vì mỗi đỉnh chỉ được duyệt nhiều nhất $1$ lần và ta sẽ mất thêm độ phức tạp $O(m)$ để duyệt tất cả các cạnh của đồ thị.
Nhìn chung, độ phức tạp của thuật toán này là $O(n + m)$.

Bài toán 2 - Đường đi dài nhất

Longestpath - Đường đi dài nhất

Đề bài

Cho đồ thị có hướng gồm $N$ đỉnh và $M$ cạnh. Các đỉnh được đánh số $1,2,…,N$ và với mỗi $i$ $(1 \le i \le M)$, cạnh có hướng thứ $i$ sẽ đi từ đỉnh $x_i$ đến đỉnh $y_i$. $G$ không chứa bất kì chu trình có hướng nào !

Tìm độ dài lớn nhất của đường đi có hướng trong $G$. Ở đây, độ dài của đường đi có hướng chính là số cạnh trong nó.

Input

Dòng thứ nhất chứa $2$ số nguyên $N,M$.
$M$ dòng tiếp theo mỗi dòng chứa hai số nguyên $x_i,y_i$ $(1 \le x_i, y_i \le N)$ (Ở đây các cặp $(x_i,y_i)$ phân biệt nhau và đề đảm bảo rằng, $G$ không chứa bất kì chu trình có hướng nào).

Output

In ra $1$ số nguyên duy nhất là độ dài lớn nhất của đường đi có hướng trong $G$.

Constraints

$2 \le N \le 10^5;1 \le M \le 10^5$.

Example

Input

3 2
1 2
2 3

Output

Note

Con đường có độ dài lớn nhất là : $1 \rightarrow 2 \rightarrow 3$.

Thuật toán

Sắp xếp Tô-pô có rất nhiều ứng dụng quan trọng, đặc biệt là áp dụng quy hoạch động trên mảng thứ tự Tô-pô.
Gọi $dp[i]$ là độ dài đường đi dài nhất bắt đầu từ đỉnh có chỉ số $i$. Ta có công thức quy hoạch động trên danh sách Tô-pô như sau:
- $dp[topo[i]]=max(dp[topo[j]] + 1)$ (Với $i = n \rightarrow 1$ và tồn tại cung từ $topo[i] \rightarrow topo[j]$).
Theo định nghĩa của thứ tự Tô-pô, chỉ tồn tại các cung từ chỉ số nhỏ đến chỉ số lớn hơn. Nên khi ta tính toán đến $dp[topo[i]]$ thì chắc chắn $dp[topo[j]]$ đều đã được tính trước đó.
Kết quả độ dài đường đi dài nhất của đồ thị là $max(dp[i])$.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 100007 .
Mảng dp[] - Mảng quy hoạch động.
Mảng visit[] - Mảng lưu trạng thái của mỗi đỉnh.
Vector g[] - Danh sách cạnh kề của mỗi đỉnh.
Vector revTopo - Danh sách nghịch đảo thứ tự Tô-pô.

#include <bits/stdc++.h>

using namespace std;

const int maxN = 1e5 + 7;

int n, m;
int visit[maxN], dp[maxN];
vector <int> g[maxN], revTopo;

void dfs(int u) {
    visit[u] = 1;
    for (auto v : g[u])
        if (!visit[v]) dfs(v);
    revTopo.push_back(u);
    visit[u] = 2;
}

main() {
    cin >> n >> m;
    while (m--) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
    }
    for (int i = 1; i <= n; ++i)
        if (!visit[i]) dfs(i);

    int ans = 0;
    for (auto u : revTopo) {
    	for (auto v : g[u])
            dp[u] = max(dp[u], dp[v] + 1);
    	ans = max(ans, dp[u]);
    }
    cout << ans;
}

Đánh giá

Khi sắp xếp Tô-pô bằng $DFS$, thuật toán sẽ trả ra danh sách nghịch đảo thứ tự Tô-pô (định nghĩa đã được viết ở mục Bài toán 1 phần Thuật toán 2). Mà ở công thức quy hoạch động, ta cần duyệt ngược lại danh sách, nên ta sẽ giữ nguyên thứ tự nghịch đảo đó và xử lí luôn trên nó.
Do đó, thay vì sử dụng ngăn xếp (stack) để đảo ngược lại danh sách. Ta sử dụng mảng động (vector) revTopo để lưu trữ lại thứ tự nghịch đảo Tô-pô đó.
Với đồ thị tổng quát, bài này sẽ trở thành bài toán $NP$.
Với $DAG$, quy hoạch động trên thứ tự Tô-pô có thể giải được trong $O(n + m)$, kể cả với trọng số dương/âm, kể cả tìm đường đi ngắn nhất/dài nhất.

Độ phức tạp

Độ phức tạp của thuật toán là $O(n + m)$.

Bài toán 3 - Fox And Names

Fox And Names - 510C Codeforces

Đề bài

Fox Ciel sẽ xuất bản một bài báo trên FOCS (Foxes Operated Computer Systems - Fox). Cô ấy nghe thấy một tin đồn: danh sách tên các tác giả trên bài báo luôn được sắp xếp theo thứ tự từ điển.

Sau khi kiểm tra, cô phát hiện ra rằng đôi khi điều đó không đúng. Trên một số bài báo, tên của các tác giả không được sắp xếp theo tiêu chuẩn thông thường của thứ tự từ điển. Nhưng sau khi sửa đổi một số thứ tự của các chữ cái trong bảng chữ cái Latin thì thứ tự tên của các tác giả được sắp xếp đúng theo thứ tự từ điển mới.

Cô ấy muốn biết liệu có tồn tại thứ tự các chữ cái trong bảng chữ cái Latin sao cho các tên trên bài báo mà cô ấy định xuất bản được sắp xếp theo thứ tự từ điển hay không. Nếu có, bạn hãy giúp cô ấy tìm ra một thứ tự thỏa mãn bất kỳ.

Thứ tự từ điển được xác định theo cách sau: Khi so sánh $2$ xâu kí tự $s$ và $t$, đầu tiên ta tìm vị trí ngoài cùng bên trái sao cho các ký tự khác nhau $(s_i≠t_i)$ rồi so sánh các ký tự $s_i$ và $t_i$ theo thứ tự của chúng trong bảng chữ cái, nếu $s_i < t_i$ thì $s$ có thứ tự từ điển nhỏ hơn $t$ và ngược lại. Còn nếu không có vị trí như vậy (tức là $s$ là tiền tố của $t$ hoặc ngược lại) thì chuỗi ngắn hơn sẽ có thứ tự từ điển nhỏ hơn.

Input

Dòng đầu tiên chứa số nguyên dương $n$ là số lượng tên các tác giả.
$n$ dòng tiếp theo, mỗi dòng chứa một chuỗi kí tự $name_i$ $(1 \le |name_i| \le 100)$ gồm các chữ cái Latin in thường là tên của tác giả thứ $i$. Tất cả tên của các tác giả đều khác nhau.

Output

Nếu tồn tại thứ tự các chữ cái mà các tên đã cho được sắp xếp theo thứ tự từ điển, hãy in ra bất kỳ thứ tự nào thỏa mãn là hoán vị của các ký tự $'a'$ $-$ $'z'$ (tức là, đầu tiên in ra chữ cái đầu tiên của bảng chữ cái đã sửa đổi, sau đó in ra chữ cái thứ hai, v.v.. ).
Nếu không, in ra một từ duy nhất: $Impossible$

Constraints

$1 \le n \le 100$.

Example

Input 1

3
rivest
shamir
adleman

Output 1

bcdefghijklmnopqrsatuvwxyz

Input 2

10
tourist
petr
wjmzbmr
yeputons
vepifanov
scottwu
oooooooooooooooo
subscriber
rowdark
tankengineer

Output 2

Impossible

Thuật toán

Giả sử, ta có hai xâu kí tự $s$ và $t$. Theo định nghĩa của thứ tự từ điển, hãy xem xét xem nếu $s < t$ thì nó cho ta biết những dữ kiện gì.
- Ví dụ: $s="abcxyz"$ và $t="abcuv"$. Để $s < t$ thì $'x'$ phải có thứ tự nhỏ hơn $'u'$ trong bảng chữ cái.
Nói cách khác, nó sẽ cho ta biết được kí tự nào sẽ phải đứng trước kí tự nào trong bảng chữ cái.
Do đó, ta có thể xây dựng một đồ thị với mỗi đỉnh tương ứng với $1$ kí tự ($'a'$ $-$ $'z'$) và mỗi cạnh có hướng từ đỉnh tương ứng với kí tự phải có thứ tự nhỏ hơn đến đỉnh tương ứng với kí tự phải có thứ tự lớn hơn đỉnh kia.
Từ đó, ta có thể sử dụng thuật toán sắp xếp Tô-pô để tìm ra $1$ thứ tự chữ cái thỏa mãn.
Nếu đồ thị không phải là $DAG$ thì không tồn tại thứ tự chữ cái nào thỏa mãn.
Lưu ý trường hợp: Nếu $s$ đứng trước $t$ trong danh sách tên và $t$ là tiền tố của $s$ thì $s$ luôn luôn có thứ tự từ điển lớn hơn $t$ nên sẽ không tồn tại thứ tự chữ cái nào thỏa mãn.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 110 .
Mảng visit[] - Mảng lưu trạng thái của mỗi đỉnh.
Vector g[] - Danh sách cạnh kề của mỗi đỉnh.
Stack topo - Danh sách thứ tự Tô-pô.

#include <bits/stdc++.h>

using namespace std;

const int maxN  = 110;

int n;
string s[maxN];
int visit[maxN];
vector <int> g[maxN];
stack <int> topo;

void printImpossible() {
    cout << "Impossible";
    exit(0);
}

// Sắp xếp Tô-pô bằng DFS
void dfs(int u) {
    visit[u] = 1;
    for (auto v : g[u]) {
        if (visit[v] == 1) printImpossible();
        if (!visit[v]) dfs(v);
    }
    topo.push(u);
    visit[u] = 2;
}

// Xây dựng các cạnh của đồ thị
void solve(string x, string y) {
    for (int i = 0; i < min(x.size(), y.size()); ++i)
        if (x[i] != y[i]) {
            g[x[i] - 'a'].push_back(y[i] - 'a');
            return;
        }

    /* Trường hợp y là tiền tố của x => x luôn lớn hơn y 
         => không có cách xếp thỏa mãn */
    if (x.size() > y.size()) printImpossible();
}

main() {
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> s[i];
        if (i) solve(s[i - 1], s[i]);
    }

    for (int i = 0; i < 26; ++i)
        if (!visit[i]) dfs(i);

    while (!topo.empty()) {
        cout << char(topo.top() + 'a');
        topo.pop();
    }
}

Đánh giá

Để tối ưu độ phức tạp, với mỗi chuỗi kí tự ta không cần phải so sánh nó với tất cả các chuỗi còn lại. Mà ta chỉ cần so sánh $2$ chuỗi kí tự liên tiếp. Vì nó sẽ luôn đúng theo tính chất bắc cầu: Nếu $s < x$ và $x < t$ thì $s < t$.

Độ phức tạp

Ở vòng for đầu tiên để xây dựng các cạnh của đồ thị, ta mất độ phức tạp $O(n * |name|)$.
Ở vòng for thứ hai để xác định thứ tự Tô-pô, ta mất độ phức tạp $O(26 + m)$. Với $m$ là số cạnh của đồ thị. Trong trường hợp xấu nhất, với mỗi cặp kí tự liên tiếp đều tạo ra $1$ cạnh thì số lượng cạnh lớn nhất có thể tạo ra là $n-1$ cạnh.
Nhìn chung, độ phức tạp của thuật toán này là $O(n * |name|)$.