Tác giả:

Nguyễn Châu Khanh - THPT Chuyên Hùng Vương - Phú Thọ
Bùi Minh Hoạt - THPT Chuyên Hùng Vương - Phú Thọ
Trần Thế Hưng - THPT Chuyên Biên Hòa - Hà Nam

Reviewer:

Đỗ Đình Đắc - Đại học Bách Khoa Hà Nội

Mở đầu

Bài viết này sẽ giúp bạn tìm hiểu về cây $DFS$ (Depth First Search Tree – DFS Tree). Cây $DFS$ là một ứng dụng quan trọng có được từ kỹ thuật duyệt đồ thị ưu tiên chiều sâu, giúp giải các bài toán tìm khớp cầu và thành phần liên thông mạnh.

Cây duyệt chiều sâu DFS (cây DFS)

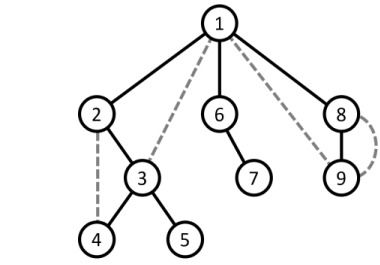
Trong quá trình $DFS$, với mỗi đỉnh $u$ ta có đỉnh $par[u]$ là số hiệu của đỉnh mà từ đỉnh đó thủ tục $DFS$ gọi đệ quy đến $u$. Xây dựng đồ thị con với các cạnh là $(par[u], u)$ ta có được một cây. Cây này được gọi là cây DFS.
Các cạnh thuộc cây $DFS$ được gọi là các “cạnh nét liền”.
Các cạnh còn lại không thuộc cây $DFS$ được gọi là các “cạnh nét đứt".

Trong đồ thị có hướng, xét các cung được thăm và không được thăm bởi $DFS$, ta có $4$ loại cung sau:
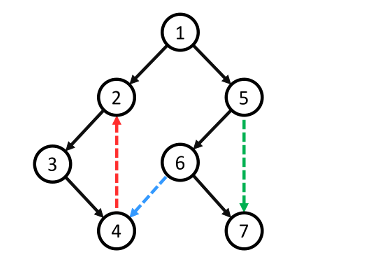
- Cung của cây $DFS$ (Tree edge): là các cung thuộc cây $DFS$ được định hướng theo chiều từ cha đến con. (ví dụ cạnh $(u,v)$ thuộc cây $DFS$ mà $u$ được thăm trước $v$ hay $u$ là cha của $v$ thì ta có cung $u \rightarrow v$ là cung của cây $DFS$). $<$ Các cung của cây $DFS$ được đánh dấu là các cạnh màu đen trong hình bên dưới $>$
- Cung xuôi (Forward edge): là các cung không thuộc cây $DFS$ và có dạng $u \rightarrow v$ trong đó $u$ là tổ tiên của $v$ trong cây $DFS$. $<$ Các cung xuôi được đánh dấu là các cạnh màu xanh lá trong hình bên dưới $>$
- Cung ngược (Back edge): là các cung không thuộc cây $DFS$ và có dạng $v \rightarrow u$ trong đó $u$ là tổ tiên của $v$ trong cây $DFS$. $<$ Các cung ngược được đánh dấu là các cạnh màu đỏ trong hình bên dưới $>$
- Cung chéo (Cross edge): là các cung không thuộc cây $DFS$ có dạng $u \rightarrow v$ trong đó $u$ và $v$ thuộc hai nhánh khác nhau của cùng một cây $DFS$. $<$ Các cung chéo được đánh dấu là các cạnh màu xanh dương trong hình bên dưới $>$
Trong đồ thị vô hướng:
- Không tồn tại cung chéo. Vì khi đỉnh $u$ được duyệt trong hàm $DFS$ ta sẽ duyệt tất cả các đỉnh $v$ kề $u$ mà $v$ chưa được thăm. Như vậy nếu tồn tại một cung chéo $(u, v)$ chứng tỏ khi duyệt đến đỉnh $u$ hoặc đỉnh $v$ ta đã không duyệt cạnh $(u, v)$.
- Vì các cạnh trên đồ thị vô hướng không được định chiều nên không thể định nghĩa $2$ loại cung xuôi và cung ngược như ở đồ thị có hướng. Do đó, ở đồ thị vô hướng, cung xuôi và cung ngược sẽ được định nghĩa như sau:
  - Cung xuôi (Forward edge): là các cung thuộc cây $DFS$. Hay còn có cách gọi khác là "cạnh nét liền" hoặc "cung của cây $DFS$".
  - Cung ngược (Back edge): là các cung không thuộc cây $DFS$. Hay còn có cách gọi khác là "cạnh nét đứt".
- Như vậy trên đồ thị vô hướng lúc này chỉ còn $2$ loại cung là cung ngược và cung xuôi (cung của cây $DFS$).

Một số mảng quan trọng trong cây DFS :

Mảng $num$[]: cho biết thứ tự duyệt $DFS$ của các đỉnh (thứ tự mà mỗi đỉnh bắt đầu duyệt).
Mảng $low$[]: Với mỗi đỉnh $u$, $low[u]$ cho biết thứ tự (giá trị $num$) nhỏ nhất có thể đi đến được từ $u$ bằng cách đi xuôi xuống theo các cạnh nét liền (các cung trên cây $DFS$) và kết thúc đi ngược lên không quá $1$ lần theo cạnh nét đứt. Ngoài ra ta cũng có thể hiểu ý nghĩa của $low[u]$ là thứ tự thăm của đỉnh có thứ tự thăm sớm nhất nằm trong cây con gốc $u$ hoặc kề cạnh với $1$ đỉnh bất kì nằm trong cây con gốc $u$.
Mảng $tail$[]: cho biết thời điểm kết thúc duyệt $DFS$ của mỗi đỉnh cũng là thời điểm duyệt xong của đỉnh đó .

Nhận xét : Các đỉnh có thứ tự thăm nằm trong khoảng từ $num[u]$ đến $tail[u]$ chính là các đỉnh nằm trong cây con gốc $u$ trong cây $DFS$.

Cách tính mảng low[], num[], tail[] :

Ý tưởng chính : Mảng $num[],tail[]$ ta có thể tính dễ dàng bằng cách $DFS$ xác định thời điểm duyệt tới và thời điểm duyệt xong của các đỉnh. Với mảng $low[]$ ta có:
- Trước hết, với $1$ đỉnh $u$ bất kì có thể tự đi tới chính nó nên ta gán $low[u]=num[u]$.
- Từ $u$ có thể đến các đỉnh $v$ kề $u$ bằng $1$ cạnh nét đứt nên ta có $low[u]=min(low[u],num[v])$ với $(u,v)$ là một cạnh nét đứt.
- Ngược lại, nếu $(u,v)$ là một cạnh nét liền và $v$ không phải cha $u$ ta có $low[u]=min(low[u],low[v])$ do từ $u$ ta có thể đi xuống $v$ sau đó đi theo con đường đã xác định ở đỉnh $v$ để tới đỉnh có thứ tự thăm là $low[v]$.
Chú ý: Giá trị thực sự của $num[u]$ được xác định khi duyệt tới đỉnh $u$ còn giá trị thực sự của $low[u],$ $tail[u]$ chỉ được xác định khi đã duyệt xong đỉnh $u$. Thời điểm duyệt tới của một đỉnh $u$ luôn diễn ra trước thời điểm duyệt tới của các đỉnh trong cây con gốc $u$ của cây $DFS$ , thời điểm duyệt xong của đỉnh $u$ luôn diễn ra sau thời điểm duyệt xong của các đỉnh trong cây con gốc $u$.
Cách thực hiện :
- Đầu tiên ta sẽ bắt đầu duyệt $DFS$ từ đỉnh gốc. Khi duyệt tới đỉnh $u$ ta sẽ cập nhật thời điểm duyệt tới. Lúc này $low[u] = num[u] =$ thứ tự duyệt DFS. Ta sẽ duyệt tất cả các con $v$ trong gốc $u$.
- Trường hợp 1: Nếu đỉnh $v$ chưa được thăm thì sau khi hoàn thành $DFS$ của $v$ thì ta sẽ cập nhật lại giá trị của $low [u]$: $low [u] = min (low[u], low[v]);$
- Trường hợp 2: Nếu đỉnh $v$ đã được thăm, thì ta sẽ cập nhật lại giá trị cho $low[u]$: $low [u] = min (low [u], num[v]);$
  - Ở trường hợp này ta không thể cập nhật $low[u] = min(low[u], low[v])$ được. Vì khi ta thăm đến đỉnh $u$ mà đỉnh $v$ đã được thăm thì tức là $(u,v)$ là một cạnh nét đứt, do đó khi đi từ $u$ tới $v$ ta đã sử dụng $1$ cạnh nét đứt nên không thể tiếp tục di chuyển nữa (theo định nghĩa của mảng $low[]$ ) suy ra ta chỉ cập nhật $low[u]=min(low[u],num[v])$.
- **Chú ý : Nếu v là cha trực tiếp của u thì ta bỏ qua không xét đến.**
- Khi đã duyệt xong đỉnh $u$ và các nút trong cây con $DFS$ gốc $u$ ta sẽ tiến hành cập nhật giá trị $tail[u]=$ thời gian duyệt DFS hiện tại.
Cài đặt :

int timeDfs = 0; // Thứ tự duyệt DFS

void dfs(int u, int pre) {
    num[u] = low[u] = ++timeDfs;
    for (int v : g[u]){
        if (v == pre) continue;
        if (!num[v]) {
            dfs(v, u);
            low[u] = min(low[u], low[v]);
        }
        else low[u] = min(low[u], num[v]);
    }
    tail[u] = timeDfs;
}

Ví dụ minh họa :
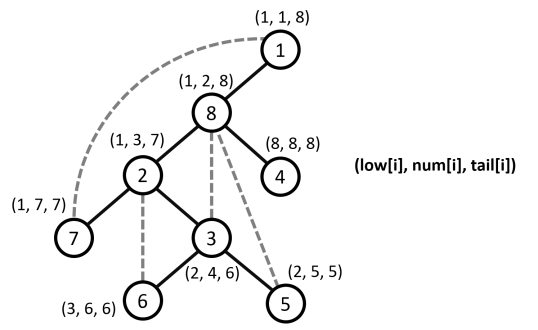
Mô tả quá trình :

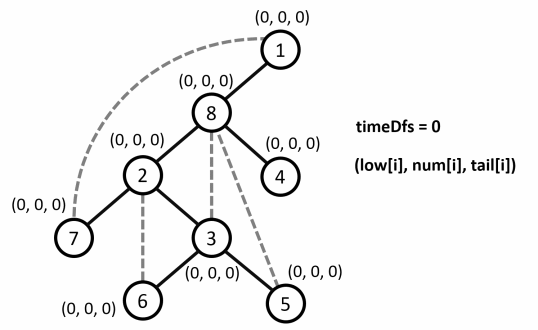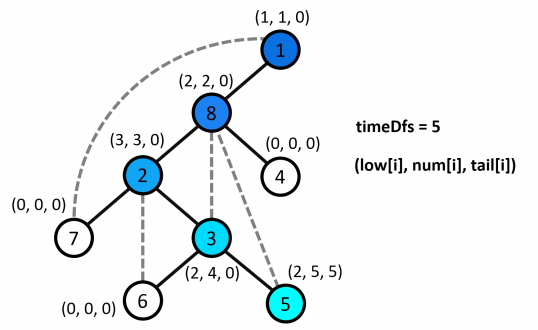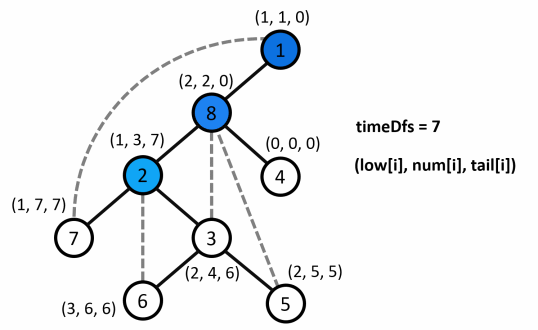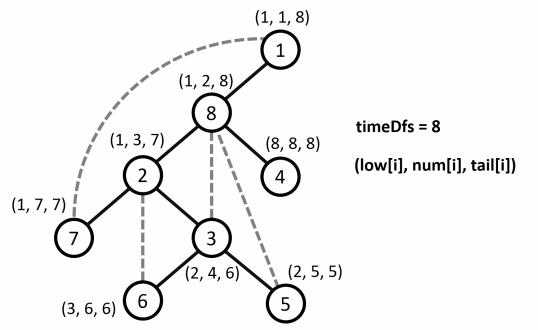
Ứng dụng cây DFS trong bài toán tìm khớp, cầu

Định nghĩa

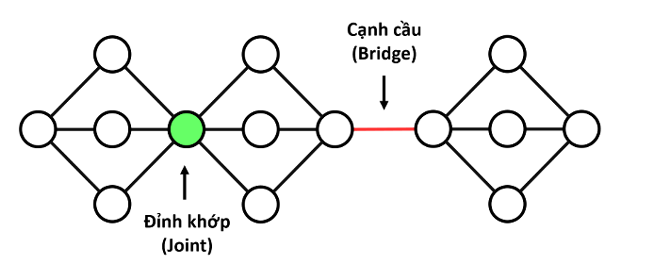
Trong đồ thị vô hướng, một đỉnh được gọi là đỉnh khớp nếu như loại bỏ đỉnh này và các cạnh liên thuộc với nó ra khỏi đồ thị thì số thành phần liên thông của đồ thị tăng lên.
Trong đồ thị vô hướng, một cạnh được gọi là cạnh cầu nếu như loại bỏ cạnh này ra khỏi đồ thị thì số thành phần liên thông của đồ thị tăng lên.

Bài toán 1

GRAPH_ - Tìm khớp và cầu (Cơ bản)

Đề bài

Xét đơn đồ thị vô hướng $G=(V, E)$ có $N$ $(1 \le N \le 10000)$ đỉnh và $M$ $(1 \le M \le 50000)$ cạnh. Người ta định nghĩa một đỉnh gọi là khớp nếu như xoá đỉnh đó sẽ làm tăng số thành phần liên thông của đồ thị. Tương tự như vậy, một cạnh được gọi là cầu nếu xoá cạnh đó sẽ làm tăng số thành phần liên thông của đồ thị.

Vấn đề đặt ra là cần phải đếm tất cả các khớp và cầu của đồ thị $G$.

Input

Dòng đầu: chứa hai số tự nhiên $N, M$.
$M$ dòng sau mỗi dòng chứa một cặp số $(u, v)$ $(u$ khác $v$, $1 \le u \le N, 1 \le v \le N)$ mô tả một cạnh của $G$.

Output

Gồm một dòng duy nhất ghi hai số, số thứ nhất là số khớp, số thứ hai là số cầu của $G$.

Example

Input

Output

4 3

Note

Các cạnh màu đỏ là cạnh cầu.
Các đỉnh màu xanh lá là đỉnh khớp.

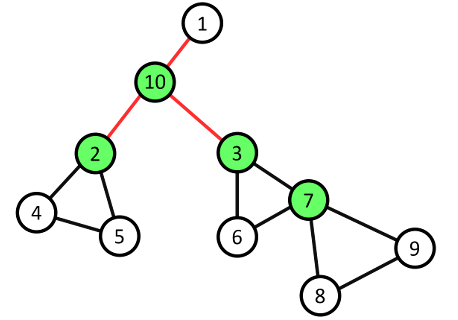
Phân tích

Tìm cạnh cầu

Dễ thấy rằng cạnh cầu của đồ thị không thể là cạnh nét đứt vì việc bỏ đi cạnh nét đứt sẽ không ảnh hưởng đến tính liên thông giữa các đỉnh của đồ thị. Do vậy cạnh cầu chỉ có thể là cạnh nét liền.
Ta sẽ xét riêng từng thành phần liên thông của đồ thị. Xét vùng liên thông $G$ như sau:
- Xét cây con gốc $v$ trong cây $DFS$ của $G$ có $u$ là cha trực tiếp của $v$. Gọi tập hợp các đỉnh thuộc cây con gốc $v$ là $A$, tập hợp các đỉnh không thuộc cây con gốc $v$ là $B$. Khi xoá đi cạnh $(u, v)$ thì giữa $2$ đỉnh bất kì thuộc cùng $1$ tập hợp vẫn có thể đến với nhau bằng các cạnh nét liền. Một đỉnh thuộc $A$ với một đỉnh thuộc $B$ muốn đi đến với nhau bằng các cạnh nét liền thì đều phải thông qua cạnh $(u, v)$.
  - Ví dụ minh họa: Xét cạnh nét liền $(7, 9)$ với đỉnh $9$ là con trực tiếp của đỉnh $7$ trên cây $DFS$. Tập đỉnh $A$ là các đỉnh được đánh dấu màu hồng. Tập đỉnh $B$ là các đỉnh được đánh dấu màu vàng. Đỉnh $11$ thuộc tập $A$ muốn đi đến đỉnh $6$ thuộc tập $B$ bằng các cạnh nét liền thì đều phải thông qua cạnh $(7, 9)$.
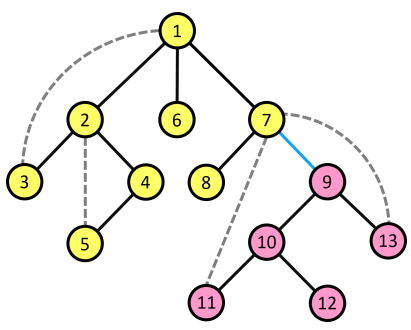
- Giả sử không có cạnh nét đứt nào nối giữa $1$ đỉnh thuộc $A$ với $1$ đỉnh thuộc $B$ thì khi xoá cạnh $(u, v)$, $G$ sẽ tách ra thành $2$ vùng liên thông $A$ và $B$. Ngược lại nếu tồn tại cạnh nét đứt nối giữa $1$ đỉnh thuộc $A$ và $1$ đỉnh thuộc $B$ đồ thị vẫn liên thông . Do đó ta chỉ cần xét xem có tồn tại cạnh nét đứt nối giữa $A$ và $B$ hay không để kết luận $(u, v)$ có phải cầu không?
- Ta có từ $v$ có thể đi đến một đỉnh $p$ nào đó có $num[p]=low[v]$ bằng cách đi theo các cung của cây $DFS$ và đi qua không quá $1$ cạnh nét đứt và $p$ có thứ tự thăm sớm nhất khi $DFS$. Nếu $p$ nằm trong $B$ thì $p$ phải là tổ tiên của $v$ cũng đồng nghĩa với việc $num[p]<num[v]$ hay $low[v]<num[v]$ (vì đồ thị không có cung chéo), nghĩa là tồn tại $1$ cạnh nét đứt nối giữa $1$ đỉnh thuộc $A$ với $1$ đỉnh thuộc $B$ (vì nếu chỉ đi bằng các cung của cây $DFS$ thì $v$ không thể tới một tổ tiên của nó).
- Do đó nếu $low[v] \ge num[v]$ chắc chắn đỉnh $p$ thuộc cây con gốc $v$ hay $p$ thuộc tập hợp $A$ khi đó không tồn tại cạnh nét đứt nối giữa $1$ đỉnh thuộc $A$ với $1$ đỉnh thuộc $B$. Tuy nhiên, ta dễ dàng nhận thấy $low[v] \le num[v]$ vì đỉnh $v$ luôn tới được chính nó.
Kết luận: Nếu $low[v] = num[v]$ thì $(u, v)$ là một cạnh cầu trong đồ thị.

Tìm đỉnh khớp

Ta sẽ xét riêng từng thành phần liên thông của đồ thị. Xét vùng liên thông $G$ như sau:
- Xét cây con gốc $u$ trong cây $DFS$ của $G$, nếu mọi nhánh con của $u$ đều có cung ngược lên tới tổ tiên của $u$ ($low[v] < num[u]$, với $v$ là tất cả các con trực tiếp của $u$ trên cây $DFS$) thì đỉnh $u$ không thể là đỉnh khớp. Bởi trong đồ thị ban đầu, nếu ta loại bỏ đỉnh $u$ đi thì từ mỗi đỉnh bất kỳ thuộc nhánh con vẫn có thể đi lên một tổ tiên của $u$, rồi đi sang nhánh con khác hoặc đi sang tất cả những đỉnh còn lại của cây nên số thành phần liên thông của đồ thị không thay đổi.
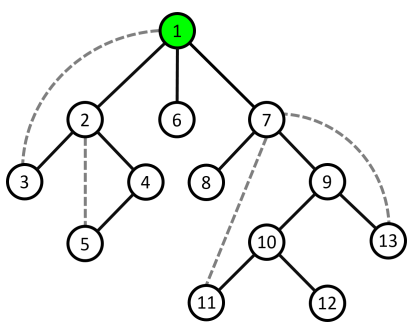
  - Ví dụ minh họa: Xét đỉnh $9$ không phải là đỉnh khớp vì cả $2$ nhánh con của nó là cây con gốc $10$ và cây con gốc $13$ trong cây $DFS$ đều có cung ngược lên tới đỉnh $7$ là tổ tiên của đỉnh $9$.
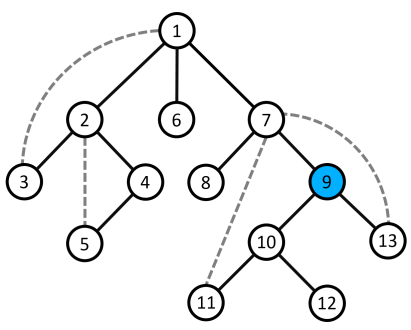
- Nếu $u$ không phải là đỉnh gốc của cây $DFS$, và tồn tại ít nhất một nhánh con trong cây con gốc $u$ không có cung ngược lên một tổ tiên của $u$ ($low[v] \ge num[u]$, với $v$ là một con trực tiếp bất kì của $u$ trên cây $DFS$) thì đỉnh $u$ là đỉnh khớp. Bởi khi đó, tất cả những cung xuất phát từ nhánh con đó chỉ có thể đi tới những đỉnh thuộc cây con gốc $u$ mà thôi, trên đồ thị ban đầu, không tồn tại cạnh nối từ những đỉnh thuộc nhánh con đó tới một tổ tiên của $u$. Vậy nên từ một đỉnh bất kì thuộc nhánh con đó muốn đi lên một tổ tiên của $u$ thì bắt buộc phải đi qua $u$ nên việc loại bỏ đỉnh $u$ ra khỏi đồ thị sẽ làm tăng số thành phần liên thông của đồ thị.
  - Ví dụ minh họa: Xét đỉnh $2$ là đỉnh khớp vì tồn tại $1$ nhánh con của nó là cây con gốc $4$ không có cung ngược lên tới tổ tiên của đỉnh $2$.
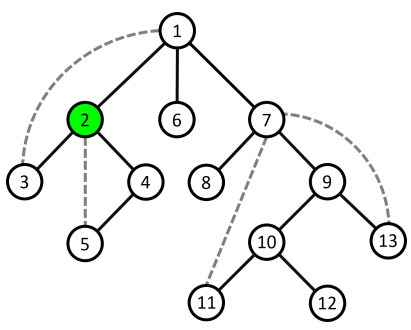
- Nếu $u$ là đỉnh gốc của cây $DFS$, thì $u$ là đỉnh khớp khi và chỉ khi $u$ có ít nhất $2$ nhánh con. Vì đồ thị không có cung chéo nên khi $u$ có $2$ nhánh con thì đường đi giữa hai đỉnh thuộc hai nhánh con đó bắt buộc phải đi qua $u$. Việc loại bỏ đỉnh $u$ ra khỏi đồ thị sẽ làm tăng số thành phần liên thông của đồ thị.
  - Ví dụ minh họa: Xét đỉnh $1$ là đỉnh khớp vì đỉnh $1$ là đỉnh gốc của cây $DFS$ và có tới $3$ nhánh con.
Kết luận: Đỉnh $u$ là đỉnh khớp khi:
- Đỉnh $u$ không phải là gốc của cây $DFS$ và $low[v] \ge num[u]$ (với $v$ là một con trực tiếp bất kì của $u$ trong cây $DFS$).
Hoặc
- Đỉnh $u$ là gốc của cây $DFS$ và có ít nhất $2$ con trực tiếp trong cây $DFS$.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 10010
Biến timeDfs - Thứ tự $DFS$
Biến bridge - Số lượng cạnh cầu
Mảng low[], num[]
Mảng joint[] - Đánh dấu đỉnh khớp
Vector g[] - Danh sách cạnh kề của mỗi đỉnh

#include <bits/stdc++.h>
 
using namespace std;
 
const int maxN = 10010;

int n, m;
bool joint[maxN];
int timeDfs = 0, bridge = 0;
int low[maxN], num[maxN];
vector <int> g[maxN];
 
void dfs(int u, int pre) {
    int child = 0; // Số lượng con trực tiếp của đỉnh u trong cây DFS
    num[u] = low[u] = ++timeDfs;
    for (int v : g[u]) {
        if (v == pre) continue;
        if (!num[v]) {
            dfs(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] == num[v]) bridge++;
            child++;
            if (u == pre) { // Nếu u là đỉnh gốc của cây DFS
                if (child > 1) joint[u] = true;
            }
            else if (low[v] >= num[u]) joint[u] = true;
        }
        else low[u] = min(low[u], num[v]);
    }
}
 
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for (int i = 1; i <= n; i++) 
        if (!num[i]) dfs(i, i);

    int cntJoint = 0;
    for (int i = 1; i <= n; i++) cntJoint += joint[i];

    cout << cntJoint << ' ' << bridge;
}

Đánh giá

Độ phức tạp của bài toán là $O(N + M)$.

Bài toán 2

NKPOLICE - Police

Đề bài

Để truy bắt tội phạm, cảnh sát xây dựng một hệ thống máy tính mới. Bản đồ khu vực bao gồm $N$ thành phố và $M$ đường nối $2$ chiều. Các thành phố được đánh số từ $1$ đến $N$.

Cảnh sát muốn bắt các tội phạm di chuyển từ thành phố này đến thành phố khác. Các điều tra viên, theo dõi bản đồ, phải xác định vị trí thiết lập trạm gác. Hệ thống máy tính mới phải trả lời được $2$ loại truy vấn sau:

$1$. Đối với hai thành phố $A$, $B$ và một đường nối giữa hai thành phố $G1$, $G2$; hỏi tội phạm có thể di chuyển từ $A$ đến $B$ nếu đường nối này bị chặn (nghĩa là tên tội phạm không thể sử dụng con đường này) không?
$2$. Đối với $3$ thành phố $A$, $B$, $C$; hỏi tội phạm có thể di chuyển từ $A$ đến $B$ nếu như toàn bộ thành phố $C$ bị kiểm soát (nghĩa là tên tội phạm không thể đi vào thành phố này) không?

Input

Dòng đầu tiên chứa $2$ số nguyên $N$ và $M$ $(2 \le N \le 100000, 1 \le M \le 500000)$, số thành phố và số đường nối.
Mỗi dòng trong số $M$ dòng tiếp theo chứa $2$ số nguyên phân biệt thuộc phạm vi $[1, N]$ - cho biết nhãn của hai thành phố nối với nhau bởi một con đường. Giữa hai thành phố có nhiều nhất một đường nối.
Dòng tiếp theo chứa số nguyên $Q$ $(1 \le Q \le 300000)$, số truy vấn được thử nghiệm trên hệ thống.
Mỗi dòng trong $Q$ dòng tiếp theo chứa $4$ hoặc $5$ số nguyên. Số đầu tiên cho biết loại truy vấn $1$ hoặc $2$.
- Nếu loại truy vấn là $1$, tiếp theo trên cùng dòng là $4$ số nguyên $A$, $B$, $G1$, $G2$ với ý nghĩa như đã mô tả. $A$ khác $B$; $G1$, $G2$ mô tả một con đường có sẵn.
- Nếu loại truy vấn là $2$, tiếp theo trên cùng dòng là $3$ số nguyên $A$, $B$, $C$ với ý nghĩa như đã mô tả. $A$, $B$, $C$ đôi một khác nhau.

Dữ liệu được cho sao cho ban đầu luôn có cách di chuyển giữa hai thành phố bất kỳ.

Output

Gồm $Q$ dòng, mỗi dòng chứa câu trả lời cho một truy vấn. Nếu câu trả lời là khẳng định, in ra "yes". Nếu câu trả lời là phủ định, in ra "no".

Example

Input

Output

yes
yes
yes
no
yes

Note

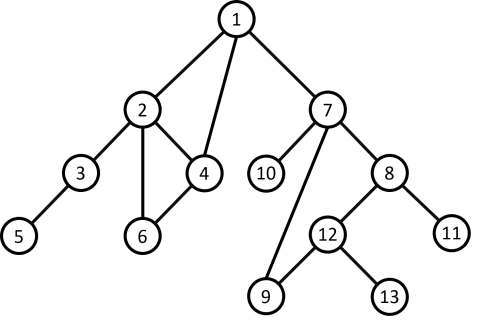
Phân tích

Để tồn tại ít nhất một cách di chuyển từ thành phố $A$ đến thành phố $B$ thì cả $2$ thành phố $A$ và $B$ phải cùng thuộc một thành phần liên thông.

Truy vấn 1

Dễ thấy rằng, nếu đường nối giữa $2$ thành phố $G1,$ $G2$ không phải là cạnh cầu thì việc loại bỏ nó đi sẽ không ảnh hưởng đến tính liên thông giữa thành phố $A$ và $B$.
Ngược lại, nếu đường nối giữa $2$ thành phố $G1,$ $G2$ là cạnh cầu thì ta phải kiểm tra xem $2$ thành phố $A$ và $B$ có thuộc cùng một thành phần liên thông sau khi loại bỏ cạnh $(G1,G2)$ hay không?
Mỗi khi loại bỏ một cạnh cầu của đồ thị vô hướng thì số thành phần liên thông của đồ thị sẽ tăng thêm $1$. Nghĩa là khi ta loại bỏ cạnh cầu $(G1,G2)$ (với $G2$ là con trực tiếp của $G1$) thì đồ thị sẽ chia ra làm $2$ thành phần liên thông:
- Thành phần liên thông thứ nhất là tập hợp các đỉnh thuộc cây con gốc $G2$ của cây $DFS$.
- Thành phần liên thông thứ nhất là tập hợp các đỉnh còn lại không thuộc cây con gốc $G2$ của cây $DFS$.
Ví dụ minh họa: Loại bỏ cạnh cầu $(1,7)$ (với đỉnh $7$ là con trực tiếp của đỉnh $1$)
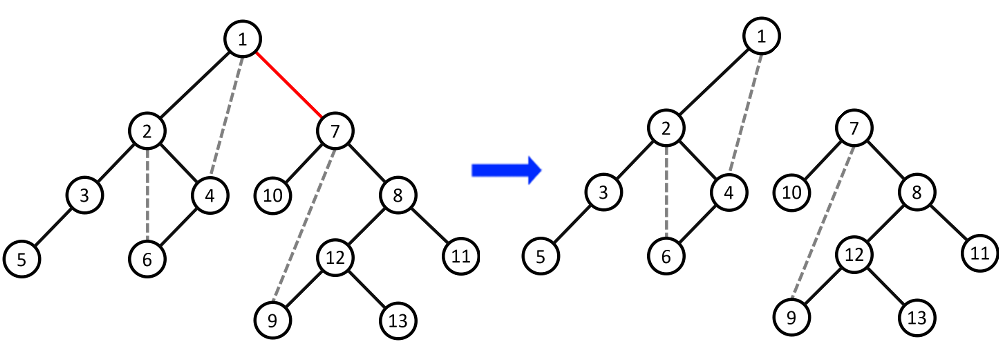
Bây giờ, ta có thể xác định vị trí của $2$ đỉnh $A,$ $B$ có nằm trong cây con gốc $G2$ hay không.
- Nếu chỉ có đúng duy nhất $1$ trong $2$ đỉnh nằm trong cây con gốc $G2$ thì $2$ thành phố $A$ và $B$ không thuộc cùng một thành phần liên thông sau khi loại bỏ cạnh $(G1,G2)$.
- Ngược lại, nếu cả $2$ đỉnh cùng nằm trong cây con gốc $G2$ hoặc cả $2$ đỉnh đều không nằm trong cây con gốc $G2$ thì $2$ thành phố $A$ và $B$ đều thuộc cùng một thành phần liên thông sau khi loại bỏ cạnh $(G1,G2)$.
Nhắc lại: Nếu $num[u] \le num[v] \le tail[u]$ thì đỉnh $v$ nằm trong cây con gốc $u$ của cây $DFS$.

Truy vấn 2

Dễ thấy rằng, nếu thành phố $C$ không phải là đỉnh khớp thì việc loại bỏ nó đi sẽ không ảnh hưởng đến tính liên thông giữa thành phố $A$ và $B$.
Ngược lại, nếu thành phố $C$ là đỉnh khớp thì ta phải kiểm tra xem $2$ thành phố $A$ và $B$ có thuộc cùng một thành phần liên thông sau khi loại bỏ đỉnh $C$ và các cạnh liên thuộc với nó đi hay không?
Vì đồ thị không có cung chéo nên khi loại bỏ đỉnh khớp $C$ ra khỏi đồ thị thì số thành phần liên thông của đồ thị tăng thêm một lượng bằng số lượng đỉnh $v$ là con trực tiếp của $C$ trong cây $DFS$ sao cho không tồn tại cung ngược (cạnh nét đứt) từ một đỉnh thuộc cây con gốc $v$ trong cây $DFS$ nối lên tổ tiên của $C$ (đồng nghĩa với việc $low[v] \ge num[C]$). Nghĩa là khi ta loại bỏ đỉnh khớp $C$ ra khỏi đồ thị thì đồ thị sẽ chia ra làm các thành phần liên thông:
- Một số thành phân liên thông, mỗi thành phần liên thông là $1$ tập hợp các đỉnh thuộc cây con gốc $v$ với $v$ là con trực tiếp của $C$ trong cây $DFS$ và $low[v] \ge num[C]$.
- Một thành phần liên thông là tập hợp tất cả các đỉnh còn lại (bao gồm các đỉnh là tổ tiên của của $C$ và các đỉnh thuộc các cây con gốc $u$ với $u$ là các con trực tiếp của $C$ trong cây $DFS$ và $low[u] < num[C]$).
Ví dụ minh họa: Loại bỏ đỉnh khớp $8$. Đỉnh $11$ và $12$ là các con trực tiếp của đỉnh $8$ trong cây $DFS$. Nhưng chỉ có cây con gốc $11$ là tách riêng ra thành $1$ thành phần liên thông riêng biệt. Còn cây con gốc $12$ thì có $1$ cung ngược nối lên đỉnh $7$ (tổ tiên của đỉnh $8$) nên số lượng thành phần liên thông của cả đồ thị chỉ tăng thêm $1$.
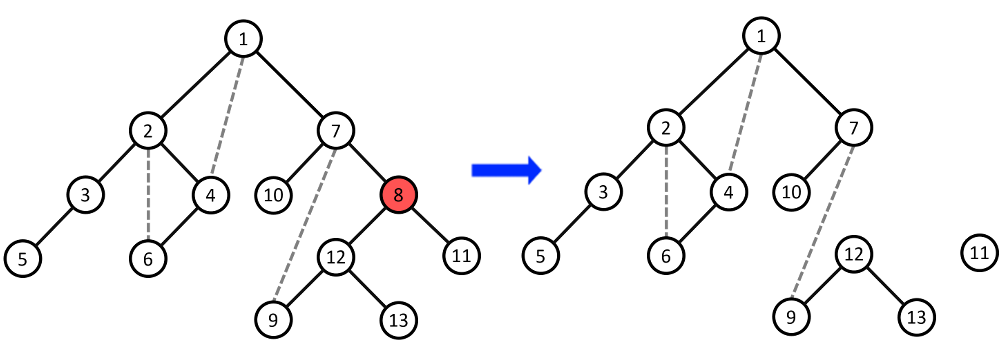
Với mỗi đỉnh $v$ là con trực tiếp của $C$ trong cây $DFS$ và $low[v] \ge num[C]$, ta kiểm tra xem nếu chỉ có đúng duy nhất $1$ trong $2$ đỉnh nằm trong cây con gốc $v$ thì $2$ thành phố $A$ và $B$ không thuộc cùng một thành phần liên thông sau khi loại bỏ đỉnh $C$ và các cạnh liên thuộc với đỉnh $C$ đi.
Ngược lại, với $v$ là các con trực tiếp của $C$ trong cây $DFS$ và $low[v] \ge num[C]$, nếu cả $2$ đỉnh $A$ và $B$ cùng nằm trong $1$ cây con gốc $v$ hoặc cả $2$ đỉnh $A$ và $B$ đều không nằm trong bất cứ $1$ cây con gốc $v$ nào cả (đồng nghĩa với việc cả $2$ đỉnh $A,$ $B$ sẽ cùng nằm trong thành phần liên thông còn lại) thì $2$ thành phố $A$ và $B$ đều thuộc cùng một thành phần liên thông sau khi loại bỏ đỉnh $C$ và các cạnh liên thuộc với đỉnh $C$ đi.
Tuy nhiên theo thuật toán trên thì với mỗi truy vấn ta sẽ phải duyệt hết tất cả các con trực tiếp của đỉnh C nên khi xử lí các truy vấn sẽ mất độ phức tạp là O(Q⋅ bậc của C). Trong trường hợp tệ nhất thì đỉnh C có thể lên đến N - 1 con trực tiếp (100000 - 1) với số lượng truy vấn Q = 300000, khiến cho thuật toán trên sẽ bị quá thời gian. Bây giờ ta cần phải cải tiến thuật toán :
Thay vì duyệt hết tất cả các con trực tiếp của $C$ để xác định được tổ tiên của $A$, tổ tiên của $B$. Ta có thể sử dụng $Sparse Table$ để tìm ra tổ tiên của đỉnh $A$ (hoặc $B$) là con trực tiếp của đỉnh $C$ nếu $A$ (hoặc $B$) nằm trong cây con $DFS$ gốc $C$. Bạn có thể tìm hiểu thêm về Sparse Table và ứng dụng của nó tại đây.
Gọi đỉnh $pa$ là tổ tiên của đỉnh $A$ và là con trực tiếp của đỉnh $C$.
Gọi đỉnh $pb$ là tổ tiên của đỉnh $B$ và là con trực tiếp của đỉnh $C$.
$A$ và $B$ thuộc cùng một thành phần liên thông sau khi loại bỏ đỉnh $C$ và các cạnh liên thuộc với đỉnh $C$ đi khi thỏa mãn một trong số các điều kiện sau:
- Nếu cả $2$ đỉnh $A$ và $B$ đều không nằm trong cây con $DFS$ gốc $C$.
- Nếu $pa = pb$ (nghĩa là cả $2$ đỉnh $A$ và $B$ đều nằm trong cây con $DFS$ gốc $pa$ ).
- Nếu $A$ không nằm trong cây con $DFS$ gốc $C$ và $B$ nằm trong cây con $DFS$ gốc $C$ sao cho $low[pb] < num[C]$ (nghĩa là có tồn tại cung ngược nối từ cây con $DFS$ gốc $pb$ lên tổ tiên của $C$ ).
- Nếu $B$ không nằm trong cây con $DFS$ gốc $C$ và $A$ nằm trong cây con $DFS$ gốc $C$ sao cho $low[pa] < num[C]$ (nghĩa là có tồn tại cung ngược nối từ cây con $DFS$ gốc $pa$ lên tổ tiên của $C$ ).
- Nếu cả $2$ đỉnh $A$ và $B$ đều nằm trong cây con $DFS$ gốc $C$ và $low[pa] < num[c]$ và $low[pb] < num[c]$ (nghĩa là cả $2$ cây con $DFS$ gốc $pa$ và cây con $DFS$ gốc $pb$ đều có cung ngược nối lên tổ tiên của $C$ )
Ngược lại, nếu không thỏa mãn tất cả các điều kiện trên thì $A$ và $B$ không thuộc cùng một thành phần liên thông sau khi loại bỏ đỉnh $C$ và các cạnh liên thuộc với đỉnh $C$ đi.
Lúc này, độ phức tạp để xử lí các truy vấn sẽ là $O(Q \cdot logN)$.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 100010
Biến timeDfs - Thứ tự $DFS$
Mảng low[], num[], tail[]
Mảng depth[] - Lưu chiều sâu của mỗi đỉnh trong cây $DFS$
Mảng p[][] - Mảng ứng dụng $Sparse Table$ với $p[i][j]$ là tổ tiên thứ $2^j$ của $i$ trong cây $DFS$
Mảng joint[] - Đánh dấu đỉnh khớp
Vector g[] - Danh sách cạnh kề của mỗi đỉnh

#include <bits/stdc++.h>

using namespace std;

const int maxN  = 100010;

int n, m, q;
int timeDfs = 0;
int low[maxN], num[maxN], tail[maxN];
int depth[maxN], p[maxN][20];
bool joint[maxN];
vector <int> g[maxN];

/* Tính mảng p */
void calP() {
    p[1][0] = 1;
    for (int j = 1; j <= 19; j++)
        for (int i = 1; i <= n; i++)
            p[i][j] = p[p[i][j - 1]][j - 1];
}

/* Tìm tổ tiên của đỉnh u là con trực tiếp của đỉnh par */
int findParent(int u, int par) {
    for (int i = 19; i >= 0; i--)
        if (depth[p[u][i]] > depth[par]) u = p[u][i];
    return u;
}

/* Tìm khớp cầu */
void dfs(int u, int pre) {
    int child = 0;
    num[u] = low[u] = ++timeDfs;
    for (int v : g[u]){
        if (v == pre) continue;
        if (!num[v]) {
            child++;
            p[v][0] = u;
            depth[v] = depth[u] + 1;
            dfs(v, u);
            low[u] = min(low[u], low[v]);
            if (u == pre) {
                if (child > 1) joint[u] = true;
            }
            else if (low[v] >= num[u]) joint[u] = true;
        }
        else low[u] = min(low[u], num[v]);
    }
    tail[u] = timeDfs;
}
 
/* Kiểm tra xem đỉnh u có nằm trong cây con DFS gốc root hay không? */
bool checkInSubtree(int u, int root) {
    return num[root] <= num[u] && num[u] <= tail[root];
}

/* Xử lí truy vấn 1 */
bool solve1(int a, int b, int g1, int g2) {
    /* Vì ta coi g2 là con trực tiếp của g1 nên khi g1 là con của g2, 
    ta phải đổi chỗ 2 giá trị g1 và g2 cho nhau */
    if (num[g1] > num[g2]) swap(g1, g2); 

    /* Kiểm tra nếu cạnh (g1, g2) không phải là cầu */
    if (low[g2] != num[g2]) return true;

    if (checkInSubtree(a, g2) && !checkInSubtree(b, g2)) return false;
    if (checkInSubtree(b, g2) && !checkInSubtree(a, g2)) return false;
    return true;
}

/* Xử lí truy vấn 2 */
bool solve2(int a, int b, int c) {
    if (!joint[c]) return true;
    int pa = 0, pb = 0;
    if (checkInSubtree(a, c)) pa = findParent(a, c);
    if (checkInSubtree(b, c)) pb = findParent(b, c);

    if (!pa && !pb) return true; 
    if (pa == pb) return true; 
    if (!pa && low[pb] < num[c]) return true; 
    if (!pb && low[pa] < num[c]) return true;
    if (pa && pb && low[pa] < num[c] && low[pb] < num[c]) return true;

    return false;
}

int main() {
    ios_base::sync_with_stdio(0); 
    cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    depth[1] = 1;
    dfs(1, 1);
    calP();
    cin >> q;
    while (q--) {
        int type, a, b, c, g1, g2;
        cin >> type;
        if (type == 1) {
            cin >> a >> b >> g1 >> g2;
            cout << (solve1(a, b, g1, g2) ? "yes\n" : "no\n");
        }
        else {
            cin >> a >> b >> c;
            cout << (solve2(a, b, c) ? "yes\n" : "no\n");
        }
    }
}

Đánh giá

Độ phức tạp của bài toán là $O(N + M + Q \cdot logN)$

Bài toán 3

KBUILD - Sửa cầu

Đề bài

Cho $N$ hòn đảo và $N - 1$ cây cầu, mỗi cây cầu nối hai hòn đảo lại với nhau. Đảm bảo rằng từ một đảo bất kì luôn có thể đến được hết mọi đảo còn lại. Pirate đưa ra một lịch trình như sau: vào mỗi ngày sẽ đi kiểm tra mọi cây cầu trên đường đi từ đảo $a$ đến đảo $b$. Hỏi sau khi Pirate thực hiện xong lịch trình đó, thì còn có bao nhiêu cây cầu chưa được kiểm tra?

Input

Dòng thứ nhất: số nguyên $N$ - số lượng hòn đảo.
$N - 1$ dòng tiếp theo: mỗi dòng chứa $2$ số nguyên $a$ và $b$ - có một cây cầu nối đảo $a$ và $b$.
Dòng thứ $N + 1$: Số nguyên $M$ - số ngày kiểm tra.
$M$ dòng tiếp theo: mỗi dòng chứa $2$ số nguyên $a$ và $b$ - ngày hôm đó, Pirate sẽ đi kiểm tra mọi cây cầu trên đường đi từ đảo $a$ đến đảo $b$.

$1 \le N, M \le 200000$

Output

Một số nguyên duy nhất thể hiện số cây cầu chưa được kiểm tra.

Input

Output

Note

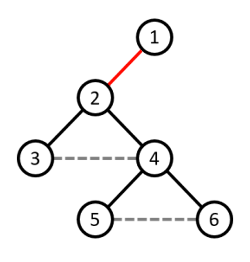
Ngày thứ nhất, Pirate kiểm tra các cây cầu $(2, 3), (2, 4)$ và $(4, 6)$. Ngày thứ hai, anh kiểm tra các cây cầu $(5, 4)$ và $(4, 6)$. Cây cầu duy nhất chưa được kiểm tra là $(1, 2)$.

Phân tích

Vì đồ thị ban đầu liên thông và có $N - 1$ cạnh nên đây là đồ thị dạng cây.

Để đánh dấu các cạnh thuộc đường đi từ đỉnh $u$ đến đỉnh $v$ trên cây, thì ta có thể thêm một cạnh $(u,v)$ vào đồ thị. Khi đó, các cạnh thuộc đường đi từ $u \rightarrow v$ trên cây sẽ nằm trong $1$ chu trình. Từ đó, bài toán sẽ quy về thành bài toán đếm số lượng cạnh cầu của đồ thị.

Ví dụ minh họa: Để dánh dấu đường đi từ đỉnh $3 \rightarrow 6$ và đường đi từ đỉnh $5 \rightarrow 6$, ta thêm cạnh $(3, 6)$, $(5, 6)$ vào đồ thị. Khi đó, đồ thị có một cạnh cầu là cạnh $(1, 2)$.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 200010
Biến timeDfs - Thứ tự $DFS$
Biến bridge - Số lượng cạnh cầu
Mảng low[], num[]
Vector g[] - Danh sách cạnh kề của mỗi đỉnh

#include <bits/stdc++.h>
 
using namespace std;
 
const int maxN = 2e5 + 10;

int n, m;
int timeDfs = 0, bridge = 0;
int low[maxN], num[maxN];
vector <int> g[maxN];
 
void dfs(int u, int pre) {
    num[u] = low[u] = ++timeDfs;
    for (int v : g[u]) {
        if (v == pre) continue;
        if (!num[v]) {
            dfs(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] == num[v]) bridge++;
        }
        else low[u] = min(low[u], num[v]);
    }
}
 
int main() {
    cin >> n;
    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        g[a].push_back(b);
        g[b].push_back(a);
    }
    cin >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        g[a].push_back(b);
        g[b].push_back(a);
    }
    dfs(1, 1);
    cout << bridge;
}

Đánh giá

Độ phức tạp của bài toán là $O(N + (N - 1 + M))$.

Ứng dụng cây DFS trong bài toán liệt kê thành phần liên thông mạnh

Định nghĩa

Một đồ thị có hướng là liên thông mạnh nếu như từ một đỉnh bất kì luôn tồn tại ít nhất một đường đi đến bất kì đỉnh nào khác.
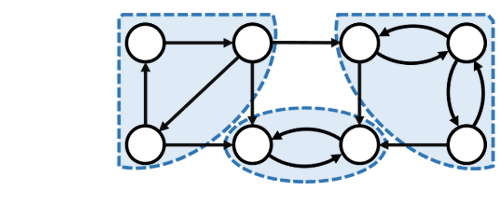
Một thành phần liên thông mạnh của một đồ thị có hướng là một đồ thị con tối đại liên thông mạnh. Nếu mỗi thành phần liên thông mạnh được co lại thành một đỉnh, thì đồ thị sẽ trở thành một đồ thị có hướng không có chu trình.
Thuật toán $Kosaraju$, thuật toán $Tarjan$, và thuật toán $Gabow$ đều có thể tìm các thành phần liên thông mạnh của một đồ thị cho trước trong thời gian tuyến tính. Tuy nhiên, các thuật toán của $Tarjan$ thường được sử dụng nhiều hơn do chúng chỉ cần thực hiện tìm kiếm theo chiều sâu một lần trong khi thuật toán của $Kosaraju$ cần hai lần.

Một số định lý quan trọng

Định lý 1: Nếu $a$, $b$ là hai đỉnh thuộc thành phần liên thông mạnh $C$ thì với mọi đường đi từ $a$ tới $b$ cũng như từ $b$ tới $a$. Tất cả đỉnh trung gian trên đường đi đó đều phải thuộc $C$. Chứng minh: Nếu $a$ và $b$ là hai đỉnh thuộc $C$ thì tức là có một đường đi từ $a$ đến $b$ và một đường khác đi từ $b$ về $a$. Suy ra với một đỉnh $v$ nằm trên đường đi từ $a$ tới $b$ thì $a$ tới được $v$, $v$ tới được $b$, mà $b$ có đường tới $a$ nên $v$ cũng tới được $a$. Vậy $v$ nằm trong thành phần liên thông mạnh chứa $a$ tức là $v$ thuộc $C$. Tương tự với một đỉnh nằm trên đường đi từ $b$ tới $a$.
Định lý 2: Với một thành phần liên thông mạnh $C$ bất kỳ, tồn tại một đỉnh $r$ thuộc $C$ sao cho mọi đỉnh của $C$ đều thuộc cây con gốc $r$ trong cây $DFS$. Chứng minh: Trước hết, nhắc lại một thành phần liên thông mạnh là một đồ thị con liên thông mạnh của đồ thị ban đầu thoả mãn tính chất tối đại tức là việc thêm vào thành phần đó một tập hợp đỉnh khác sẽ làm mắt đi tính liên thông mạnh.

Trong số các đỉnh của $C$, chọn $r$ là đỉnh được thăm đầu tiên theo thuật toán tìm kiếm theo chiều sâu. Ta sẽ chứng minh $C$ nằm trong nhánh $DFS$ gốc $r$. Thật vậy, với một đỉnh $v$ bất kỳ của $C$, do $C$ liên thông mạnh nên phải tồn tại một đường đi từ $r$ tới $v$: $(r = x_0, x_1,…, x_k = v)$

Từ định lý $1$, tất cả các đỉnh $x_1, x_2,…, x_k$ đều thuộc $C$ nên chúng sẽ phải thăm sau đỉnh $r$. Khi thủ tục $DFS(r)$ được gọi thì tất cả các đỉnh $x_1, x_2,…, x_k$ đều chưa thăm; vì thủ tục $DFS(r)$ sẽ liệt kê tất cả những đỉnh chưa thăm đến được từ $r$ bằng cách xây dựng nhánh gốc $r$ của cây $DFS$, nên các đỉnh $x_1, x_2,…, x_k = v$ sẽ thuộc nhánh gốc $r$ của cây $DFS$. Bởi chọn $v$ là đỉnh bất kỳ trong $C$ nên ta có điều phải chứng minh.

Đỉnh $r$ trong chứng minh định lý - đỉnh thăm trước tất cả các đỉnh khác trong $C$ - gọi là chốt của thành phần $C$. Mỗi thành phần liên thông mạnh có duy nhất một chốt. Xét về vị trí trong cây tìm kiếm $DFS$, chốt của một thành phân liên thông là đỉnh nằm cao nhất so với các đỉnh khác thuộc thành phần đó, hay nói cách khác: là tiền bối của tất cả các đỉnh thuộc thành phần đó.
Định lý 3: Luôn tìm được đỉnh chốt $a$ thỏa mãn: Quá trình tìm kiếm theo chiều sâu bắt đầu từ $a$ không thăm được bất kỳ một chốt nào khác. (Tức là nhánh $DFS$ gốc $a$ không chứa một chốt nào ngoài $a$) chẳng hạn ta chọn $a$ là chốt được thăm sau cùng trong một dây chuyền đệ quy hoặc chọn $a$ là chốt thăm sau tất cả các chốt khác. Với chốt $a$ như vậy thì các đỉnh thuộc nhánh $DFS$ gốc $a$ chính là thành phần liên thông mạnh chứa $a$. Chứng minh: Với mọi đỉnh $v$ nằm trong nhánh $DFS$ gốc $a$, xét $b$ là chốt của thành phần liên thông mạnh chứa $v$. Ta sẽ chứng minh $a = b$. Thật vậy, theo định lý $2$, $v$ phải nằm trong nhánh $DFS$ gốc $b$. Vậy $v$ nằm trong cả nhánh $DFS$ gốc $a$ và nhánh $DFS$ gốc $b$. Giả sử phản chứng rằng $a$ khác $b$ thì sẽ có hai trường hợp xảy ra:
- Trường hợp 1: Nhánh $DFS$ gốc $a$ chứa nhánh $DFS$ gốc $b$, có nghĩa là thủ tục $DFS(b)$ sẽ do thủ tục $DFS(a)$ gọi tới, điều này mâu thuẫn với giả thiết rằng $a$ là chốt mà quá trình tìm kiếm theo chiều sâu bắt đầu từ $a$ không thăm một chốt nào khác.
- Trường hợp 2: Nhánh $DFS$ gốc $a$ nằm trong nhánh $DFS$ gốc $b$, có nghĩa là $a$ nằm trên một đường đi từ $b$ tới $v$. Do $b$ và $v$ thuộc cùng một thành phần liên thông mạnh nên theo định lý $1$, $a$ cũng phải thuộc thành phần liên thông mạnh đó. Vậy thì thành phần liên thông mạnh này có hai chốt $a$ và $b$. Điều này vô lý.
Theo định lý $2$, ta đã có thành phân liên thông mạnh chứa $a$ nằm trong nhánh $DFS$ gốc $a$, theo chứng minh trên ta lại có: Mọi đỉnh trong nhánh $DFS$ gốc $a$ nằm trong thành phân liên thông mạnh chứa $a$. Kết hợp lại được: Nhánh $DFS$ gốc $a$ chính là thành phần liên thông mạnh chứa $a$.

Bài toán 4

TJALG - Tìm TPLT mạnh

Đề bài

Cho đồ thị $G(V, E)$ có hướng $N$ $(1 \le N \le 10^4)$ đỉnh, $M$ $(1 \le M \le 10^5)$ cung. Hãy đếm số thành phần liên thông mạnh của $G$.

Input

Dòng đầu tiên là $N, M$.
$M$ dòng tiếp theo mô tả một cung của $G$.

Output

Gồm một dòng duy nhất là số TPLT mạnh.

Examples

Input

3 2
1 2
2 3

Output

Input

Output

Thuật toán Tarjan

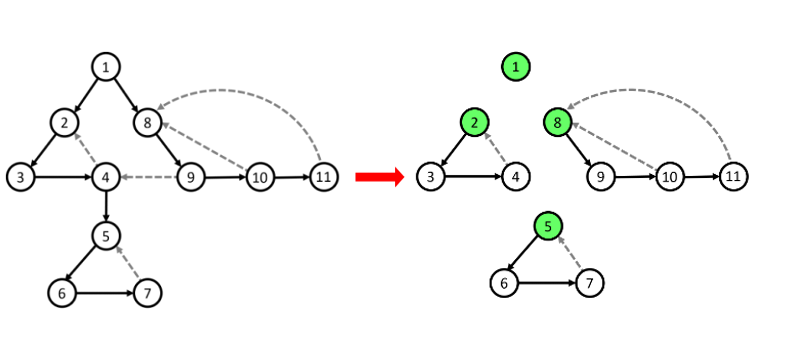
Thuật toán Tarjan được xây dựng dựa trên các dữ kiện sau:

Tìm kiếm $DFS$ tạo ra cây/ rừng $DFS$
Các thành phần liên thông mạnh tạo thành các cây con của cây $DFS$.
Nếu ta có thể tìm được đỉnh gốc của các cây con như vậy, ta có thể in/ lưu trữ tất cả các nút trong cây con đó (bao gồm cả đỉnh gốc) và đó sẽ là một thành phần liên thông mạnh $(Strongly$ $Connected$ $Components$ - $SCC).$
Không có cung ngược từ $SCC$ này sang $SCC$ khác (Có thể có các cung chéo, nhưng các cung chéo sẽ không được sử dụng trong khi xử lý đồ thị).

Mô tả thuật toán

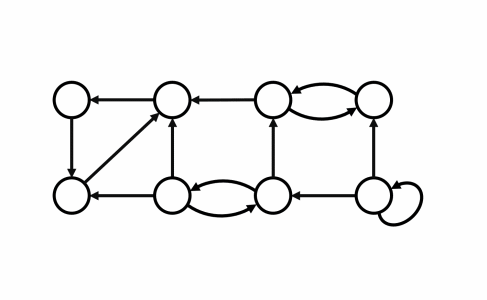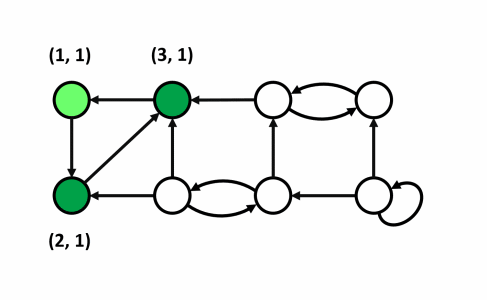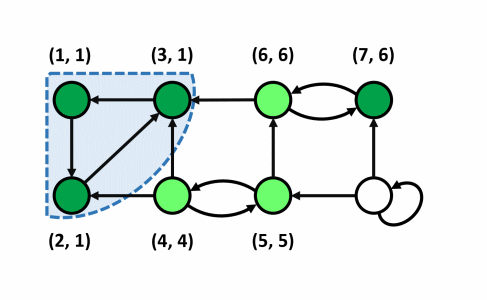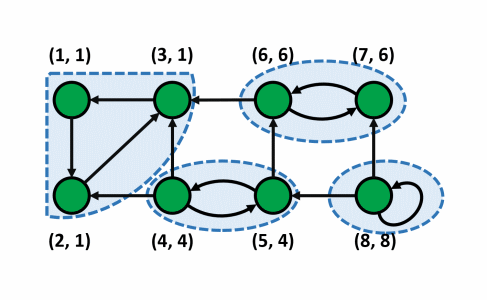
Ý tưởng

Nhận xét: Xét cây con gốc $u$ trong cây $DFS$. Gọi tập hợp các đỉnh thuộc cây con gốc $u$ là $A$, tập hợp các đỉnh không thuộc cây con gốc $u$ là $B$. Nếu tồn tại $1$ đỉnh $x$ thuộc $A$ tới được $1$ đỉnh $y$ thuộc $B$ thì $y$ phải có thứ tự thăm sớm hơn $u$. Vì nếu $y$ được thăm sau $u$ ta có thể duyệt từ $u$ qua $x$ tới $y$ khi đó $y$ sẽ trở thành con của $u$.
Đầu tiên ta thực hiện $DFS$ kết hợp tính mảng $low[], num[]$ như đã trình bày ở trên. Song song với việc này, khi duyệt tới đỉnh $u$ ta sẽ thực hiện đẩy $u$ vào $stack$.
Khi đã duyệt xong đỉnh $u$ (sau khi duyệt hết toàn bộ các đỉnh nằm trong cây con $DFS$ gốc $u$), nếu $num[u] = low[u]$ thì đây chính là đỉnh có thứ tự thăm sớm nhất của một thành phần liên thông mạnh.
Khi đó ta sẽ loại bỏ tất cả các đỉnh trong thành phần liên thông mạnh này ra khỏi đồ thị và các đỉnh này là các đỉnh đang nằm trên $u$ trong $stack$ hiện tại vì các đỉnh này chính là các đỉnh nằm trên cây con gốc $u$ trong cây $DFS$ do các nút được đẩy vào $stack$ theo thứ tự thăm.
Mặt khác, giả sử ta có đỉnh $x$ thuộc cây con gốc $u$ và $x$ thuộc một thành phần liên thông mạnh không chứa $u$ có đỉnh có thứ tự thăm sớm nhất là $y$, dễ thấy $y$ phải là con của $u$ nên thời điểm duyệt xong của $y$ sớm hơn $u$ chứng tỏ $y$ và thành phần liên thông mạnh chứa nó sẽ bị loại bỏ trước đó không còn trong $stack$ nữa (nếu $y$ không phải con $u$ thì vô lí vì ta đang xét mọi đỉnh trong cây con gốc $u$ chưa được xác định nằm trong thành phần liên thông mạnh nào hiện tại không tới được các đỉnh không nằm trong cây con gốc $u$).
Ta sẽ đánh dấu tất cả các đỉnh thuộc thành phần liên thông mạnh này bằng $1$ mảng để sau này không xét lại đỉnh đấy nữa. Đồng thời, ta loại bỏ cách đỉnh này ra khỏi $stack$ để không làm ảnh hưởng tới các đỉnh khác vẫn còn nằm trong đồ thị.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 100010
Biến timeDfs - Thứ tự $DFS$
Biến scc - Số lượng thành phần liên thông mạnh
Mảng low[], num[]
Mảng deleted[] - Đánh dấu các đỉnh đã bị xóa
Vector g[] - Danh sách cạnh kề của mỗi đỉnh
Ngăn xếp st - Lưu lại các đỉnh trong thành phần liên thông mạnh

#include <bits/stdc++.h>

using namespace std;

const int maxN = 100010;

int n, m;
int timeDfs = 0, scc = 0;
int low[maxN], num[maxN];
bool deleted[maxN];
vector <int> g[maxN];
stack <int> st;

void dfs(int u) {
    num[u] = low[u] = ++timeDfs;
    st.push(u);
    for (int v : g[u]) {
    	if (deleted[v]) continue;
        if (!num[v]){
            dfs(v);
            low[u] = min(low[u], low[v]);
        }
        else low[u] = min(low[u], num[v]);
    }
    if (low[u] == num[u]) {
        scc++;
        int v;
        do {
            v = st.top(); 
            st.pop();
            deleted[v] = true;
        }
        while (v != u);
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
    }
    for (int i = 1; i <= n; i++)
        if (!num[i]) dfs(i);

    cout << scc;
}

Đánh giá

Độ phức tạp của thuật toán $Tarjan$ là $O(N + M)$

Bài toán 5

KCOLLECT - Thu hoạch

Đề bài

Khu vườn của Pirate có hình chữ nhật, và được chia thành $M \cdot N$ ô vuông bằng nhau. Trong mỗi ô vuông có một cây thuộc một loại quả khác nhau, đánh số từ $0$ đến $9$. Những con số này thể hiện giá trị kinh tế của các loại cây. Tuy nhiên, nhìn mặt con Robot trái cây này có vẻ ngu ngu nên trong lần đầu tiên thử việc, Pirate muốn test AI của nó. Cụ thể là Robot phải tuân theo các quy định sau:

Tại mỗi ô, Robot chỉ có thể đi sang hướng đông hoặc hướng nam sang ô kề cạnh.
Có một số ô đặc biệt mà tại đó Robot có thể đi được thêm hướng tây hoặc hướng bắc sang ô kề cạnh (chỉ một trong hai).
Robot không được đi vào những ô có cây dừa.
Robot được đi qua một ô nhiều lần. Khi đi qua một ô, Robot phải hái hết quả ở cây trong ô đó. Lợi nhuận thu được sẽ bằng chỉ số của loại cây vừa được thu hái. Và sau này, không thể đạt thêm lợi nhuận gì từ ô đó nữa.

Xuất phát từ ô ở góc tây bắc của khu vườn, hãy giúp Robot trái cây xác định hành trình để đạt được lợi nhuận tối đa.

Input

Dòng thứ nhất: ghi hai số nguyên $M$ và $N$ - kích thước của khu vườn.
$M$ dòng tiếp theo: mỗi dòng ghi $N$ kí tự liên tiếp nhau mô tả khu vườn: + '0' - '9': các loại trái cây; + '#': cây dừa; + 'W': được quyền đi theo hướng tây; + 'N': được quyền đi theo hướng bắc.

Output

Ghi một số nguyên duy nhất là lợi nhuận tối đa đạt được.

Example

Input

2 3
264
3WW

Output

Note

Robot sẽ đi theo hành trình như sau $(1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3) \rightarrow (2, 2) \rightarrow (2, 1)$ (ô $(i, j)$ là ô ở dòng $i$ và cột $j$). Tổng lợi nhuận sẽ là $2 + 6 + 4 + 3 = 15$.

Phân tích

Tại sao ta không thể Quy hoạch động ngay được? Theo đề bài, ở tại mỗi ô Robot có thể đi sang hướng đông (đi sang phải) hoặc hướng nam (đi xuống dưới) sang ô kề cạnh. Tuy nhiên ở những ô đặc biệt thì Robot có thể đi thêm hướng tây (đi sang trái) hoặc hướng bắc (đi lên trên). Và một ô có thể được Robot đi qua nhiều lần. Chính vì lí do này thế nên cách đi của Robot sẽ tạo thành chu trình. Khi đường đi tạo thành chu trình thì khi ta QHĐ sẽ bị vô hạn.
Làm sao để đường đi không tạo thành chu trình? Một đồ thị có hướng là liên thông mạnh nếu như có đường từ bất kì đỉnh này tới bất kì đỉnh nào khác. Một thành phần liên thông mạnh của một đồ thị có hướng là một đồ thị con tối đại liên thông mạnh. Nếu mỗi thành phần liên thông mạnh được co lại thành một đỉnh, thì đồ thị sẽ trở thành một đồ thị có hướng không có chu trình. Khi dựng đồ thị mới ta sẽ có cung $(u,v)$ nếu tồn tại một đỉnh $x$ bất kì nằm trong thành phần liên thông mạnh mang nhãn $u$ có cung tới một đỉnh $y$ bất kì nằm trong thành phần liên thông mạnh mang nhãn $v$.
Mấu chốt của bài toán này là: Tìm ra được các thành phần liên thông mạnh, co từng thành phần liên thông mạnh thành $1$ đỉnh. Lúc này đồ thị mới sẽ là đồ thị DAG (Directed Acyclic Graph). Đây là đồ thị "một đi không trở lại", vậy nên ta dễ dàng QHĐ trên đồ thị DAG.
Công thức QHĐ trên đồ thị DAG: $f[u] = max(f[v]) + C[u]$ với mọi $u$ có cung trực tiếp đi tới $v$; trong đó $C[u]$ là tổng giá trị kinh tế của đỉnh $u$ , $f[u]$ là tổng giá trị kinh tế lớn nhất khi ta xuất phát tại $u$ và kết thúc tại $1$ đỉnh bất kì vì ta có thể đi từ $u$ sang $v$ rồi đi theo đường đi tối ưu xuất phát tại $v$ ($u,v$ ở đây là các đỉnh trên đồ thị $DAG$ được tạo ra).

Cài đặt

Cấu trúc dữ liệu:

Để có thể dễ dàng cài đặt thì ta sẽ sử dụng kĩ thuật "Biến mảng 2 chiều thành mảng 1 chiều" nhằm mục đích lưu giá trị ô $(i, j)$ vào ô $(i - 1) \cdot N + j$.
Hằng số maxN = 100010
Hằng số INF = 1000000007
Biến timeDfs - Thứ tự $DFS$
Biến scc - Số lượng thành phần liên thông mạnh
Mảng a[] - Lưu các dữ liệu vào.
Mảng val[] - Lưu giá trị kinh tế của loại cây.
Mảng totalScc[] - Lưu tổng giá trị kinh tế của từng thành phần liên thông mạnh.
Mảng root[] - Lưu ô $(i, j)$ thuộc thành phần liên thông nào? Ta sẽ lấy thứ tự của thành phần liên thông làm đỉnh ảo trong đồ thị $DAG$.
Mảng low[], num[]
Mảng deleted[] - Đánh dấu các đỉnh đã bị xóa
Mảng f[] - Mảng quy hoạch động
Vector g[] - Lưu đồ thị ban đầu.
Vector h[] - Lưu đồ thị mới (đồ thị DAG).

#include <bits/stdc++.h>

using namespace std;
 
const int maxN = 100010;
const int INF  = 1e9 + 7;
 
int dx[] = {0, -1, 0, 1, 0};
int dy[] = {0,  0, 1, 0,-1};

int m, n;
char a[maxN];
int val[maxN], totalScc[maxN];

/* Lưu đồ thị ban đầu*/
vector <int> g[maxN];

/* Lưu đồ thị mới*/
vector <int> h[maxN];

/* Kỹ thuật "Biến mảng 2 chiều thành mảng 1 chiều" */
int getId(int i, int j){
    return (i - 1) * n + j;
}

/* Kiểm tra ô (i, j) có được đi vào không? */
bool check(int i, int j) {
    if (a[getId(i, j)] == '#') return false;
    return (i >= 1 && j >= 1 && i <= m && j <= n);
}

/* Tìm thành phần liên thông mạnh*/
int root[maxN];
int low[maxN], num[maxN];
bool deleted[maxN];
int timeDfs = 0, scc = 0;
stack <int> st;
 
void dfs(int u) {
    low[u] = num[u] = ++timeDfs;
    st.push(u);
    for (int v : g[u]) {
        if (deleted[v]) continue;
        if (!num[v]) {
            dfs(v);
            low[u] = min(low[u], low[v]);
        }
        else low[u] = min(low[u], num[v]);
    }
 
    if (num[u] == low[u]) {
        scc++;
        int v;
        do {
            v = st.top();
            st.pop();
            deleted[v] = true;

            /* Tính tổng giá trị kinh tế của thành phần liên thông */
            totalScc[scc] += val[v];

            /*Đỉnh scc sẽ là đỉnh ảo đại diện cho v trong đồ thị DAG*/
            root[v] = scc;
        } while (v != u);
    }
}
 

/* Quy hoạch động trên đồ thị DAG */
int f[maxN];

int solve(int u) {
    if (h[u].empty()) return totalScc[u];
    if (f[u] != -1) return f[u];
    int cur = -INF;
    for (int v : h[u]) cur = max(cur, solve(v) + totalScc[u]);
    return f[u] = cur;
}
 
int main() {
    /* Xử lý dữ liệu đầu vào */
    cin >> m >> n;
    for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= n; ++j) {
            int u = getId(i, j);
            cin >> a[u];
            val[u] = (a[u] >= '0' && a[u] <= '9') ? a[u] - '0' : 0;
        }

    /* Xây dựng đồ thị ban đầu */ 
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            int u = getId(i, j);
            if (a[u] == '#') continue;
            if (check(i, j + 1)) g[u].push_back(getId(i, j + 1));
            if (check(i + 1, j)) g[u].push_back(getId(i + 1, j));

            if (a[u] == 'W' && check(i, j - 1)) 
                g[u].push_back(getId(i, j - 1));
            
            if (a[u] == 'N' && check(i - 1, j)) 
                g[u].push_back(getId(i - 1, j));
        }
    }

    /* Tìm thành phần liên thông mạnh*/ 
    for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= n; ++j){
            int u = getId(i, j);
            if (!num[u] && check(i, j)) dfs(u);
        }

    /* Xây dựng đồ thị mới */ 
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (!check(i, j)) continue;
            int u  = getId(i, j);
            int ru = root[u];
            for (int v : g[u]) {
                int rv = root[v];
                if (ru != rv) {
                /* Có cung đi từ ru đến rv trên đồ thị mới do đỉnh 
                u trong TPLTM ru đi được tới đỉnh v trong TPLTM rv*/
                    h[ru].push_back(rv);
                }
            }
        }
    }
    fill(f, f + m * n + 1, -1);
    cout << solve(root[getId(1, 1)]);
}

Đánh giá

Độ phức tạp của bài toán là $O(N \cdot M)$

Bài tập vận dụng

Khớp cầu

WEATHER - Điều kiện thời tiết

CRITICAL - Thành phố trọng yếu

BCACM11E - Phương án bắn pháo

SAFENET2 - Mạng máy tính an toàn

REFORM - VOI 2015 Day 1 - Kế hoạch cải tổ

Thành phần liên thông mạnh

Ralph and Mushrooms

Checkposts

MESSAGE - Truyền tin

TREAT - Cho kẹo hay bị phá nào

Cây DFS (Depth-First Search Tree) và ứng dụng

Mở đầu

Cây duyệt chiều sâu DFS (cây DFS)

Ứng dụng cây DFS trong bài toán tìm khớp, cầu

Định nghĩa

Bài toán 1

Đề bài

Phân tích

Tìm cạnh cầu

Tìm đỉnh khớp

Cài đặt

Đánh giá

Bài toán 2

Đề bài

Phân tích

Truy vấn 1

Truy vấn 2

Cài đặt

Đánh giá

Bài toán 3

Đề bài

Phân tích

Cài đặt

Đánh giá

Ứng dụng cây DFS trong bài toán liệt kê thành phần liên thông mạnh

Định nghĩa

Một số định lý quan trọng

Bài toán 4

Đề bài

Thuật toán Tarjan

Mô tả thuật toán

Ý tưởng

Cài đặt

Đánh giá

Bài toán 5

Đề bài

Phân tích

Cài đặt

Đánh giá

Bài tập vận dụng

Khớp cầu

Thành phần liên thông mạnh