Biên soạn: Đỗ Việt Anh

Table of Contents

0. Kiến thức cần biết
1. Ứng dụng
2. Phát biểu bài toán
3. cách giải bài toán
4. Bài toán liên quan
5. Một số bài để luyện tập
6. Nguồn tham khảo

0. Kiến thức cần biết

Để có thể hiểu được bài viết bạn đọc cần biết các khái niệm về lý thuyết đồ thị và bài viết giới thiệu về bài toán luồng cực đại trên mạng

1. Ứng dụng

Chính tên bài toán đã cho thấy một ứng dụng của nó đó là tính lượng nước có thể vận chuyển giữa hai địa điểm(điểm phát và điểm thu) trong hệ thống
Ứng dụng thứ 2 đó là tính toán lưu lượng giao thông của hệ thống đường trong thành phố

Trên đây là 2 ứng dụng dễ thấy của bài toán rất mong được góp ý để làm phong phú nội dung của mục này

2. Phát biểu bài toán

Cho một mạng (network) có dạng một đồ thị vô hướng $G=(E,V)$ ($V$ là tập đỉnh, $E$ là tập cạnh) có:

$e=(u,v) \in E$ như một kênh chuyển tải nước từ $u$ đến $v$ có sức chứa(capacity) $c(e)=c[u,v]$ (hay là giá trị luồng tối đa có có thể qua $e$)
Một đỉnh phát $s$ (source)
Và một đỉnh thu $t$ (sink)

Yêu cầu: với mỗi kênh truyền tải $e=[u,v]\in E$ cần xác định giá trị $f[u,v] (f[u,v]\le c[u,v])$ được gọi là luồng (flow) trên kênh $e$, sao cho $\sum_{v∈V} f[v,u]=\sum_{w\in V} f[u,w]$ ($\forall u\in V/\{s,t\}$) (tổng luồng đi vào bằng tổng luồng đi ra). Hơn thế nữa $f(s,V)=\sum_{v\in V} f[s,v]$ là lớn nhất.

Lưu ý: ở đây $f(s, V)$($=\sum_{u\in V} f[s,u]$) là một hàm trong khi $f[s,u]$ là một giá trị

hình dưới đây biểu diễn một luồng cực đại trên mạng và mỗi cạnh của nó được gán nhãn là $f[u,v]/c[u,v]$ (giá trị dòng chảy và sức chứa của kênh)

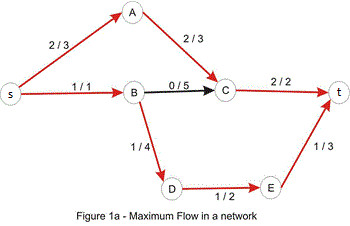
3. cách giải bài toán

Trước hết để giải được bài toán ta biết hai khái niệm mạng thặng dư (residual network) và đường tăng luồng (augment path)

3.1 mạng thặng dư - residual network

Mạng thặng dư $G'(E',V')$ của mạng $G(E,V)$ cho biết sức chứa còn lại trên mạng $G(E,V)$ khi đã gửi một số luồng $f^{*}$ qua nó và được xây dựng như sau:

Tập đỉnh $V'= V$
Mỗi cạnh $e(u,v) ∈ E$ có giá trị luồng là $f[u,v]$ và sức chứa $c[u,v]$ tương ứng với 2 cạnh trong $E'$:
- $e'(u,v)$(cạnh xuôi) có $f'[u,v]=f[u,v]$,$c'[u,v]=c[u,v]$
- Và $e'(v,u)$(cạnh ngược) có $f'[v,u]=-f[u,v]$ và $c'[v,u]=0$

(Có thể thấy tập cạnh xuôi trên $G'$ chính là tập cạnh của $G$). Hình dưới đây sẽ diễn tả một đồ thị G và mạng thặng dư $G$' của nó

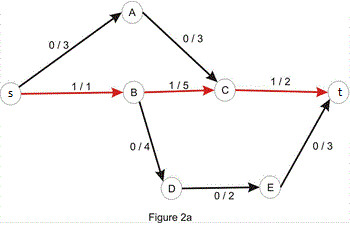
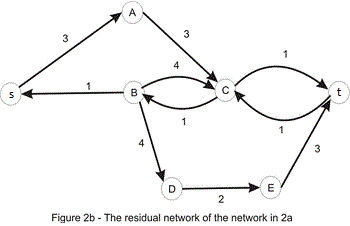
3.2 đường tăng luồng - augment path

Đường tăng luồng là một đường đi đơn từ đỉnh phát $s$ (source) đến đỉnh thu $t$ (sink) trong mạng thặng dư $G'$ mà kênh trên đường đi chưa bị bão hòa ( $f'[u,v] < c'[u,v]$, một kênh $e'(u,v)$ được gọi là bão hòa nếu $f'(u,v)=c'(u,v)$).

3.3 ví dụ

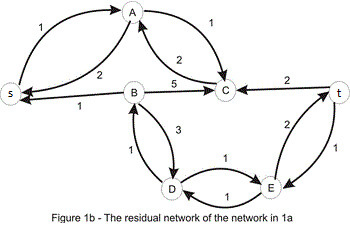
bằng việc xem xét đường tăng luồng s_A_C_t trên mạng thặng dư $G'$ chúng ta có thể tăng luồng lên 1 vì s_A và A_C có thể cho một luồng có giá trị là 3 nhưng C_t chỉ có thể cho một luồng 1 đi qua, do đó ta sẽ lấy giá trị nhỏ nhất trên đường đi để thực hiện tăng giá trị luồng. Sau khi tăng luồng lên một ta có hình như sau:

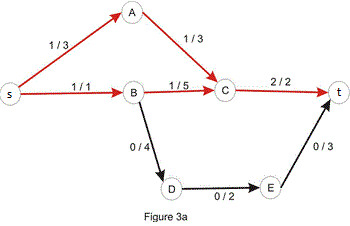
sau khi tăng luồng ta được một mạng mới với tổng giá trị luồng là 2 nhưng trong ví dụ 1.a ta thấy tổng luồng là 3 do đó luồng như trên vẫn có thể tăng luồng thêm nữa. Vậy một câu hỏi là ta sẽ tăng luồng như thế nào? hãy nhìn vào mạng thặng dư 3.b của đồ thị 3.a dưới đây, trong hình dưới mối cạnh của $G'$ sẽ được gán nhãn bằng $c'[u,v] - f'[u,v]$

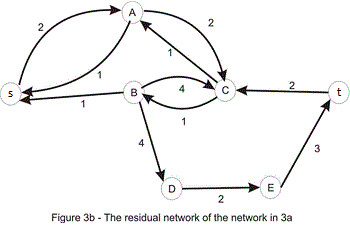
Ta có thể thấy từ $s$ đến $t$ tồn tại một đường đi đơn (đường tăng luồn): s_A_C_B_D_E_t, ta sẽ sử dụng đường đi này để tăng các giá trị trên đường đi này một lượng bằng sức chứa nhỏ nhất (sức chứa của C_B nhỏ nhất và bằng 1), hình 1.b dưới đây là mạng thặng dư tương ứng của 3.a sau khi được tăng luồng

3.4 Thuật toán Ford–Fulkerson

Từ ví dụ trên ta có thể đi đến thuật toán như sau:

$bước (1)$: Tạo mạng thặng dư $G'$ tương ứng cho mạng $G$ ban đầu

$bước (2)$: tìm một đường tăng luồng trên mạng thặng dư $G'$

nếu không tồn tại đường tăng luồng $\rightarrow$ kết thúc thuật toán
nếu tồn một đường tăng luồng $\rightarrow$ thực hiện tăng luồng trên mạng thặng dư và quay trở lại $bước (2)$ Khi thuật toán kết thúc $f(s,V')$ chính là giá trị luồng cực đại cần tìm.

Đến đây bạn đã có thể dùng thuật toán tìm kiếm trên đồ thị DFS (deep first search) hoặc BFS(breath first search) để tìm đường tăng luồng và cập nhật mạng thặng dư thuật toán này có độ phức tạp bằng số lần tăng luồng ($f^{*}$) nhân với độ phức tạp của thật toán tìm kiếm đồ thị-$O(E)$ và bằng $O(|f^{*}|.E)$. Sau đâu là code của thuật toán trên:

Lưu ý: Trong các thuật toán dưới đây ta sẽ gọi trace[u] là điển đi đến được u trong đường tăng luồng, nếu không có đỉnh nào đến được u trace[u] sẽ có giá trị là $-1$

def dfs(int u, sink):
    # đánh dấu u đã được thăm
    visited[u] = True

    # duyệt hết các đỉnh v có thể đến được từ u hay thỏa mãn điều kiện c[u][v] - f[u][v] > 0
    for( v in VertecesCanComeFromU ):
        if not visited[v]:
            trace[v] = u

def find_augment_from_to(int source, int sink):
    """
        brief: hàm này sẽ tìm một đường tăng luồng từ source đến sink
        return: 
            - Nếu có một đường tăng luồng trả về True
            - Nếu không có đường tăng luồng nào trả về False
    """
    # khởi tạo mảng đánh dấu visited ( false nếu chưa thăm, true nếu đã thăm)
    fill(all(visited), False)
    # dùng thuật toán dfs tìm đường tăng luồng
    dfs(source, sink)
    return visited[sink]

def increase_flow(int minCapacity, int source, int sink)
    """
        brief: thủ tục tăng luồng lên một giá trị minCapacity theo đường tăng luồng từ source đên sink
    """
    # khởi tạo minCapacity vô cùng lớn
    minCapacity = inf

    # lấy khả năng thông qua nhỏ nhất trên đường tăng luồng để tăng luồng
    u = sink
    while u != source:
        previousVertex = trace[u]
        minCapacity = min(minCapacity, c[previousVertex][u]-f[previousVertex][u])
        u = previousVertex

    # tăng luồng
    while sink != source:
        previousVertex = trace[sink]
        f[previousVertex][sink] += minCapacity
        f[sink][previousVertex] -= minCapacity
        sink = previousVertex

# Trong khi vẫn tồn tại đường tăng luồng
while find_augment_from_to(s,t):
    # tăng luồng
    increase_flow(s, t)

Để hiểu rõ hơn về thuật toán và cách chứng minh bạn có thể đọc tiếp các phần sau:

3.5 tính đúng dắn

Để có thể chứng minh được thuật toán trước hết ta cần biết 2 khái niệm lát cắt $s-t$ và lát cắt $s-t$ hẹp nhất trên mạng thặng dư G'

3.5.1 Lát cắt $s-t$

Lát cắt là một các phân hoạch tập các đỉnh $V'$ trong mạng thặng dư $G'$ thành 2 tập $X$ và $Y$ thỏa mãn đỉnh phát $s$ thuộc $X$ và đỉnh thu $t$ thuộc $Y$. Ta có giá trị luồng của lát cắt là $f(X, Y)$ và $c(X, Y)$ (trong đó $f(X,Y)=\sum_{u \in X}\sum_{v \in Y} f'[u,v]$ và $c(X,Y)=\sum_{u \in X}\sum_{v \in Y} c'[u,v]$) ta có thể chứng mình được 2 điều sau:

$f(X, Y) \le c(X, Y)$
Giá trị luồng $f(s,V') = f(X,Y)$

3.5.2 Lát cắt s-t hẹp nhất

lát cắt hẹp nhất là lát cắt có f(X,Y) là nhỏ nhất (hay f(X, Y) = c(X, Y)). Từ khái niệm lát cắt và lát cắt nhỏ nhất ta có thể dẫn đến cách chứng minh sau

3.5.3 chứng minh

ta có thể chứng minh 3 nhận định sau là tương đương:

$(1)$ $f^{*}$ là luồng cực đại trên mạng
$(2)$ Mạng thặng dư $G'$ không có đường tăng luồng
$(3$) tồn tại lát cắt $s-t$ hẹp nhất trên $G'$

Chứng minh:

$(1) \rightarrow (2)$: vì nếu tồn tại đường tăng luồng thì ta có thể tăng luồng để được một luồng mới lớn hơn $\rightarrow$ trái với $(1)$
$(2) \rightarrow (3)$: nếu giả sử không tồn tại lát cắt hẹp nhất ta có thể tìm được đường tăng luồng $\rightarrow$ $(2)$ sai (phần này có thể coi như một bài tập cho bạn đọc)
$(3) \rightarrow (1)$: Ta có thể thấy $f(s,V') = f(X, Y) \le c(X, Y)$, do đó $f(s,V')$ là luồng cực đại vì nếu tồn tại một luồng $f^{*} > f(s,V')$ sẽ vô lý với nhận xét trong mục lát cắt $s-t$ 3.5.1 .

3.6 Các thuật toán tìm đường tăng luồng

Như đã nói $O(|f^{*}|.E)$ là độ phức tạp của thuật toán Ford-Fulkerson nó phụ thuộc 2 yếu tố là tìm đường tăng luồng $O(E)$ và số lần tăng luồng $f^{*}$ do đó ta có thể tối ưu 1 trong 2 hoặc cả 2 nếu muốn thuật toán chạy nhanh hơn. Trong mục này ta sẽ tìm hiểu cách để có thể giảm được số lần tăng luồng $f^{*}$ điều này phụ thuộc nhiều vào việc chọn đường tăng luồng nào để tăng, các phương pháp dưới đây đều có độ phức tạp là $O(|f^{*}|.E)$ nhưng đa số các trường hợp sẽ có độ tốt tăng dần theo thứ tự trình bày sau:

3.6.1 Sử dụng thuật toán thuật toán tìm kiếm theo chiều sâu(Deep First Search-DFS)

Thuật toán này có ưu điểm là dễ dàng cài đặt nhưng thông thường số lần tăng luồng là khá lớn. Code đã được trình bày ở cuối mục 3.4. Mặc dù cài đặt có đơn giản nhưng sẽ có thời gian chạy thực tế lớn hơn thuật toán BFS dưới đây.

3.6.2 Sử dụng thuật toán tìm kiếm theo chiều rộng(Breadth First Search-BFS)

mặc dù dùng bfs để tìm đường mở có độ phức tạp lý thuyết bằng với khi tìm đường tăng luồng bằng dfs nhưng thuật toán này trong thực tế lại nhanh hơn nhiều độ phức tạp lý thuyết.

def bfs(int source, int sink):
    # khởi tạo mảng đánh dấu visited ( false nếu chưa thăm, true nếu đã thăm)
    fill(all(visited), False)

    # đẩy source vào queue
    queue.push(source)
    # đánh dấu source
    visited[source] = True

    while queue.not_empty():
        u = queue.pop()

        # duyệt hết các đỉnh v có thể đến được từ u hay thỏa mãn điều kiện c[u][v] - f[u][v] > 0
        for( v in VertecesCanComeFromU ):
            if !visited[v]:
                queue.push(v)
                visited[v] = True
                trace[v] = u
    
def find_augment_from_to(int source, int sink):
    """
        brief: hàm này sẽ tìm một đường tăng luồng từ source đến sink
        return: 
            - Nếu có một đường tăng luồng trả về True
            - Nếu không có đường tăng luồng nào trả về False
    """
    # Dùng thuật toán bfs tìm đường tằng luồng từ source đến sink
    bfs(source, sink)

    return visited[sink]

3.6.3 Sử dụng thuật toán tìm kiếm ưu tiên(Priority First Search-PFS)

Thuật toán này tìm ra đường mở có thể tăng luồng lớn nhất trong tất cả các đường mở và khá giống với thuật toán Dijkstra tìm đường đi ngắn nhất vì cùng sử dụng hàng đợi ưu tiên priority_queue, nó được chứng minh có độ phức tạp là $E * logU$ với U là khả năng thông qua lớn nhất và độ phức tạp của hàng đợi ưu tiên (priority_queue) là $E*logE$ nhưng cũng như khi dùng bfs để tìm đường mở pfs cũng chạy nhanh hơn lý thuyết rất nhiều

def pfs(int source, int sink):
    # khởi tạo mảng đánh dấu visited ( false nếu chưa thăm, true nếu đã thăm)
    fill(all(visited), False)
    # 
    fill(all(minCapacity), 0)

    # đẩy source vào priority_queue pq với giá trị luồng cực đại là vô cùng lớn
    pq.push([source, inf])

    while queue.not_empty():
        uAndMinCapacity = queue.pop()
        minC = uAndMinCapacity[1]
        u = uAndCapacity[0]

        visited[u] = True

        # duyệt hết các đỉnh v có thể đến được từ u hay thỏa mãn điều kiện c[u][v] - f[u][v] > 0
        for( v in VertecesCanComeFromU ):
            if !visited[v] && min(minC, c[u][v]-f[u][v]) > minCapacity[v]:
                minCapacity[v] = c[u][v]-f[u][v]
                queue.push([v, minCapacity[v]])
                trace[v] = u
    
def find_augment_from_to(int source, int sink):
    """
        brief: hàm này sẽ tìm một đường tăng luồng từ source đến sink
        return: 
            - Nếu có một đường tăng luồng trả về True
            - Nếu không có đường tăng luồng nào trả về False
    """
    # Dùng thuật toán bfs tìm đường tằng luồng từ source đến sink
    pfs(source, sink)

    return visited[sink]

4. Bài toán liên quan

Mạng với nhiều điểm phát và nhiều điểm thu

Cho một mạng gồm $n$ đỉnh với $p$ điểm phát $A_{1}, A_{2},..,A_{p}$ và q điểm thu $B_{1}, B_{2},…,B_{p}$. Mỗi cung của mạng được gán khả năng thông qua là số nguyên. Các đỉnh phát chỉ có cung đi ra và các đỉnh thu chỉ có cung đi vào. Một luồng trên mạng này là một phép gán cho mỗi cung một số thực gọi là luồng trên cung đó không vượt quá khả năng thông qua và thoả mãn với mỗi đỉnh không phải đỉnh phát hay đỉnh thu thì tổng luồng đi vào bằng tổng luồng đi ra. Giá trị luồng bằng tổng luồng đi ra từ các đỉnh phát = tổng luồng đi vào các đỉnh thu. Hãy tìm luồng cực đại trên mạng.

Cặp ghép cực đại trên đồ thị 2 phía

Một lớp học khiêu vũ có N bạn nam $B_{1},B_{2},…,B_{N}$ và M bạn nữ $G_{1},G_{2},…,G_{M}$ ở buổi học đầu tiên các bạn nam được yêu cầu mời một bạn nữ làm bạn nhảy cùng trong cả khóa học theo khảo sát chúng ta biết được bảng giá trị like[i][j], like[i][j]=True nếu bạn nữ Gj chấp nhận lời đề nghị từ bạn nam Bi và like[i][j]=False ngược lại nếu bạn gái Gj không chấp nhận lời mời từ bạn nam Bi. Bạn hãy xác định số cặp nhảy nhiều nhất có thể của lớp học.

Tập đại diện

Một lớp học có n bạn nam, n bạn nữ. Cho m món quà lưu niệm, (n ≤ m). Mỗi bạn có sở thích về một số món quà nào đó. Hãy tìm cách phân cho mỗi bạn nam tặng một món quà cho một bạn nữ thoả mãn:

Mỗi bạn nam chỉ tặng quà cho đúng một bạn nữ
Mỗi bạn nữ chỉ nhận quà của đúng một bạn nam
Bạn nam nào cũng đi tặng quà và bạn nữ nào cũng được nhận quà, món quà đó phải hợp sở thích của cả hai người.
Món quà nào đã được một bạn nam chọn thì bạn nam khác không được chọn nữa

Mạng với khả năng thông qua của các đỉnh và các cạnh

Cho một mạng với đỉnh phát A và đỉnh thu B. Mỗi cung (u, v) được gán khả năng thông qua c[u, v]. Mỗi đỉnh v khác với A và B được gán khả năng thông qua d[v]. Một luồng trên mạng được định nghĩa như trước và thêm điều kiện:

tổng luồng đi vào đỉnh v không được vượt quá khả năng thông qua d[v] của đỉnh đó.

Hãy tìm luồng cực đại trên mạng.

Lát cắt hẹp nhất:

Cho một đồ thị liên thông gồm n đỉnh và m cạnh, hãy tìm cách bỏ đi một số ít nhất các cạnh để làm cho đồ thị mất đi tính liên thông

5. Một số bài để luyện tập

6. Nguồn tham khảo

Lý thuyết đồ thị - DSAP Textbook của thầy Lê Minh Hoàng - Đại học sư phạm Hà Nội
Topcoder - maximum flow section 1

Luồng cực đại trên mạng - Maxflow network