Z-function
Người viết: Nguyễn Nhật Minh Khôi - Đại học Khoa học Tự nhiên - ĐHQG-HCM
Reviewer:
- Trần Quang Lộc - ITMO University
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Nguyễn Phú Bình - THPT chuyên Hùng Vương, Bình Dương
- Nguyễn Hoàng Vũ - THPT chuyên Phan Bội Châu, Nghệ An
Tham khảo: cp-algorithm
Định nghĩa
Trong blog này, chúng ta sẽ tìm hiểu về hàm $Z$ (Z-function) của một chuỗi $S$ và những ứng dụng của nó.
Cho một chuỗi $S$ độ dài $n$, ký hiệu là $S[0\ldots n - 1]$, ta có hàm $Z$ tương ứng là một mảng $z[0\ldots n - 1]$, với $z[i]$ là độ dài tiền tố chung lớn nhất của chuỗi $S[0 \ldots n - 1]$ và $S[i \ldots n - 1]$.
Ở đây, ta sẽ quy ước hai điều: một là chuỗi và mảng sẽ mặc định bắt đầu từ $0$, hai là $z[0] = 0$, ta có thể hiểu quy ước này nghĩa là chuỗi con xét ở đây phải là chuỗi con nghiêm ngặt (tức không tính chính nó).
Ví dụ hàm $z$ với $S = aaabaab$:
| i | S[0..n-1] | S[i..n-1] | z[i] |
|---|---|---|---|
| 0 | $aaabaab$ | $aaabaab$ | $0$ (quy ước) |
| 1 | $\color{red}{aa}abaab$ | $\color{red}{aa}baab$ | $2$ |
| 2 | $\color{red}{a}aabaab$ | $\color{red}{a}baab$ | $1$ |
| 3 | $aaabaab$ | $baab$ | $0$ |
| 4 | $\color{red}{aa}abaab$ | $\color{red}{aa}b$ | $2$ |
| 5 | $\color{red}{a}aabaab$ | $\color{red}{a}b$ | $1$ |
| 6 | $aaabaab$ | $b$ | $0$ |
Thuật toán ngây thơ
Thuật toán ngây thơ rất đơn giản, với mọi $i$, ta sẽ tìm $z[i]$ bằng cách vét cạn, bắt đầu với $z[i] = 0$ và tăng $z[i]$ lên cho đến khi gặp kí tự đầu tiên không trùng và lưu ý $i + z[i]$ phải hợp lệ (bé hơn hoặc bằng vị trí cuối chuỗi $n - 1$). Thuật toán được trình bày như sau:
vector<int> z_function(string s) {
int n = s.length();
vector<int> z(n);
for (int i = 1; i < n; ++i)
while (i + z[i] < n && s[z[i]] == s[i + z[i]])
++z[i];
return z;
}Thuật toán tối ưu
Để tối ưu thuật toán, ta có một nhận xét: nếu ta đã tính được $z[k]$ (ở đây chỉ xét $z[k] > 0$), ta có thông tin rằng đoạn $S[k \ldots k + z[k] - 1]$ khớp với đoạn $S[0 \ldots z[k] - 1]$. Tận dụng thông tin này, ta có thể rút ngắn quá trình tính các $z[i]$ ở sau ($i > k$). Để ngắn gọn, tạm thời đặt $l = k, r = k + z[k] - 1$. Cụ thể có hai trường hợp:
- $i \leq r$: vì đoạn $s[l \ldots r]$ giống với đoạn $s[0 \ldots r - l]$, do đó ta không cần duyệt lại đoạn $s[i\ldots r]$ mà chỉ cần lấy lại $z[i - l]$ đã tính trước đó, tuy nhiên $z[i - l]$ có thể lớn hơn $r - i + 1$, tức vượt biên $r$ đã duyệt, do đó ta chỉ lấy khởi tạo của $z[i]$ là:
$z[i] = \texttt{min}(r - i + 1, z[i - l])$
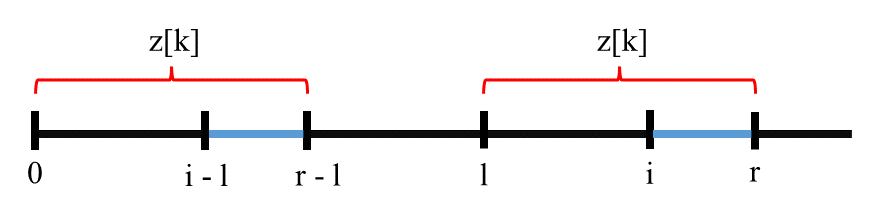
- $i > r$: khi đó $i$ nằm ngoài vùng ta đã kiểm tra, khi đó ta không thể tận dụng gì nên chỉ khởi tạo $z[i] = 0$ và làm theo thuật toán ngây thơ.
Từ nhận xét này, ta thấy rằng nếu $k + z[k] - 1$ càng lớn, tức $r$ nào càng lớn thì ta càng có cơ hội khởi tạo được $z[i]$ lớn hơn (tức ít phải xét lại hơn). Do đó trong quá trình tính $z$ ta sẽ duy trì hai biến $l$ và $r$ với ý nghĩa đoạn $[l,r]$ là đoạn thoả $S[l \ldots r] = S[0 \ldots r - l]$ và $r$ là lớn nhất. khi đó, mỗi lần xét một $z[i]$ mới ta sẽ khởi tạo $z[i]$ như đã đề cập ở trên. Sau khi tính xong $z[i]$, ta sẽ cập nhật lại $l$ và $r$ với đoạn $[i, i + z[i] - 1]$ mới tính. Từ đó ta có thuật toán cải tiến như sau:
vector<int> z_function(string s) {
int n = s.length();
vector<int> z(n);
for (int i = 1, l = 0, r = 0; i < n; ++i) {
// khoi tao z[i] theo thuat toan toi uu
if (i <= r)
z[i] = min(r - i + 1, z[i - l]);
// tinh z[i]
while (i + z[i] < n && s[z[i]] == s[i + z[i]])
++z[i];
// cap nhat doan [l,r]
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
return z;
}Lưu ý rằng ở đây ta khởi tạo $l = r = 0$ để đảm bảo đây là một đoạn không chứa bất kỳ $i > 0$ nào.
Để chứng minh thuật toán tối ưu ta sẽ xem xét số phép tính trong vòng lặp while. Dễ thấy rằng, mỗi vị trí $i$ sẽ chỉ có hai trường hợp sau:
- $i > r$: khi này nếu $z[i] = 0$ thì vòng lặp while sẽ chỉ lặp một lần, $r$ sẽ được giữ nguyên. Ngược lại, nếu $z[i] > 0$ thì sau khi chạy, do $i > r$ nên chắc chắn $i + z[i] - 1 > r$, khi đó ta sẽ tăng $r$ lên thành $i + z[i] - 1$.
- $i \leq r$: ta có hai trường hợp nhỏ nữa:
- $z[i - l] < r - i + 1$: do ta đã kiểm soát được $s[l \ldots r]$ nên rõ ràng $z[i]$ sẽ không thể tăng lên nữa, do đó vòng lặp while sẽ dừng sau lần kiểm tra điều kiện đầu tiên, $r$ sẽ được giữ nguyên.
- $z[i - l] \geq r - i + 1$: khi đó, do ta chưa biết phía sau đoạn $s[i \ldots r]$ có khớp tiếp không, nên có thể vòng while sẽ phải chạy thêm nữa. Tuy nhiên, khi chạy xong, $r$ chắc chắn chỉ có thể giữ nguyên (không có thêm ký tự khớp nên $z[i] = r - i + 1$) hoặc tăng lên (có thêm ký tự khớp nên $z[i] > r - i + 1$).
Từ hai nhận xét này, ta thấy một điều quan trọng, đó là phép toán ++z[i] luôn làm tăng $r$. Mà $r$ chỉ có thể tăng chứ không giảm, hơn nữa giá trị $r$ tối đa chỉ có thể là $n - 1$ nên số lần tăng của $r$ chỉ có thể là $n - 1$. Từ hai điều này, ta kết luận rằng vòng lặp while chỉ lặp không quá $n - 1$ lần phép ++z[i] trong suốt quá trình tính $z$. Do đó, độ phức tạp của thuật toán đã cho là $O(n)$.
Kĩ thuật hai con trỏ cũng là một cách giải thích khác cho thuật toán này. Ta có thể tưởng tượng $l$ và $r$ là hai con trỏ luôn tăng, việc thực hiện phép ++z[i] trong vòng lặp while cũng tương đương với việc tăng $r$ lên một đơn vị ($l$ lúc này sẽ được gán lại bằng $i$ hiện tại). Khi đó, vì $r$ không bao giờ tăng quá $n - 1$ lần nên phép ++z[i] cũng không bao giờ thực hiện quá $n - 1$ lần, ta kết luận thuật toán có độ phức tạp $O(n)$.
Một số ứng dụng
So khớp chuỗi
Cho chuỗi $S$ độ dài $n$ và $T$ độ dài $m$, ta cần tìm chuỗi con liên tục trong $S$ sao cho chuỗi con đó bằng với chuỗi $T$. Bạn đọc có thể nộp bài ở VNOJ.
Thuật toán trong trường hợp này rất đơn giản, ta chỉ cần tạo chuỗi mới $P = T + \diamond + S$, khi đó ta chỉ cần tính $z$ của chuỗi $P$ mới này và chọn ra các $i$ có $z[i] = m$. Ở đây, $\diamond$ là một ký tự đặc biệt dùng để phân tách $T$ và $S$ trong chuỗi $P$, đảm bảo $z[i]$ không vượt quá độ dài của $T$, ký tự $\diamond$ này phải thoả điều kiện là không nằm trong cả chuỗi $S$ và chuỗi $T$.
Giả sử $ \diamond = \texttt{#} $, thuật toán có thể cài đặt bằng ngôn ngữ C++ như sau:
vector<int> string_matching(string s, string t) {
string p = t + '#' + s;
int m = t.length();
int n = s.length();
vector<int> z = z_function(p);
vector<int> res;
for (int i = m + 1; i <= m + n; ++i) {
// tim duoc dap an va them vao vector res
if (z[i] == m)
res.push_back(i - m - 1);
}
return res;
}Số lượng chuỗi con phân biệt trong một chuỗi $O(n^2)$
Cho chuỗi $S$ có độ dài $n$, ta cần tìm số lượng chuỗi con phân biệt của $s$.
Chúng ta sẽ giải quyết bài này một cách tuần tự như sau: biết được số lượng chuỗi con phân biệt của chuỗi $s$ hiện tại là $k$, ta thêm một ký tự $c$ vào, đếm xem có bao nhiêu chuỗi con phân biệt mới của $s + c$ và cập nhật lại $k$.
Gọi $t = reverse(s + c)$ là chuỗi thu được bằng cách viết ngược từ ký tự cuối tới ký tự đầu của $s + c$, ta nhận xét rằng các chuỗi con phân biệt mới sẽ luôn kết thúc tại $c$. Khi đó nhiệm vụ của chúng ta tương ứng với việc đếm xem có bao nhiêu tiền tố của $t$ không xuất hiện ở bất cứ đâu trong $t$. Ta sẽ làm điều đó bằng cách tính hàm $z$ của $t$ và tìm giá trị lớn nhất $z_{max}$. Rõ ràng là các chuỗi con có độ dài $z_{max}$ và nhỏ hơn đều xuất hiện lần thứ hai đâu đó trong $t$, còn các chuỗi con có độ dài lớn hơn $z_{max}$ sẽ chưa xuất hiện. Do đó, số lượng chuỗi con mới xuất hiện là $length(t) - z_{max}$.
Vậy, thuật toán của chúng ta sẽ có vòng lặp $i$ tăng từ $0$ đến $n - 1$, tại mỗi $i$, biết được số lượng chuỗi phân biệt hiện tại là $k$, ta sẽ tính xem số lượng chuỗi con mới xuất hiện khi thêm $s[i]$ vào chuỗi $s[0\ldots i - 1]$ đã xét và cập nhật lại số lượng chuỗi phân biệt. Độ phức tạp của thuật toán này là $O(n^2)$.
int num_substr(string s) {
vector<int> z = z_function(s);
string tmp;
int k = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
tmp = s[i] + tmp;
vector<int> z = z_function(tmp);
int zmax = *max_element(z.begin(), z.end());
k += (i + 1) - zmax;
}
return k;
}Chú ý rằng thay vì thêm dần dần ký tự vào cuối chuỗi $s$, ta có thể làm điều ngược lại là bỏ dần các ký tự ở đầu chuỗi $s$, độ phức tạp của hai cách làm này là tương đương nhau.
Period finding
Cho chuỗi $S$ độ dài $n$, ta cần tìm chuỗi $t$ ngắn nhất sao cho ta có thể tạo ra $s$ bằng cách ghép một hoặc nhiều bản sao của chuỗi $t$ lại.
Cách giải bài này là tính hàm $z$ cho $S$, sau đó xét các $i$ mà $n$ chia hết cho $i$ và dừng lại ở $i$ đầu tiên thoả $i + z[i] = n$. Khi đó kết quả của chúng ta là $i$.
int length_compress(string s) {
vector<int> z = z_function(s);
int n = s.length();
for (int i = 1; i < n; ++i) {
if (n % i == 0 && i + z[i] == n)
return i;
}
return n;
}Tính đúng đắn của thuật toán đã được chứng minh ở phần Compressing a string trong link này.