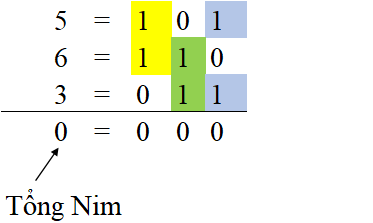Lý thuyết trò chơi
Người viết: Nguyễn Nhật Minh Khôi
Reviewer chính: Trần Quang Lộc, Hồ Ngọc Vĩnh Phát
Trong thực tế, có rất nhiều loại trò chơi khác nhau, tuy nhiên trong bài viết này, chúng ta sẽ chỉ giới hạn trong các trò chơi tổ hợp cân bằng vì độ phổ biến của nó trong lập trình thi đấu.
Giới thiệu: trò chơi bốc sỏi
Trước khi đi vào các định nghĩa, chúng ta sẽ đi qua một ví dụ để hiểu được vấn đề mà lý thuyết trò chơi với trò chơi tổ hợp cân bằng giải quyết.
Phát biểu trò chơi
Hai bạn An và Bình đang chơi bốc sỏi, trò chơi được phát biểu như sau: cho một đống sỏi có $n$ viên sỏi, hai bạn sẽ luân phiên bốc sỏi từ đống sỏi, mỗi lượt chỉ được bốc $1$, $2$ hoặc $3$ viên sỏi, người lấy được viên sỏi cuối cùng sẽ là người chiến thắng. Biết rằng An đi trước, Bình đi sau. Hãy tìm một chiến thuật để An có thể chiến thắng trò chơi.
Cách giải
Ta sẽ tiếp cận bài toán bằng cách giải những trường hợp đơn giản trước, sau đó rút ra quy luật chung cho trường hợp tổng quát.
Với $n = 1, 2$ hoặc $3$, An luôn chiến thắng bằng cách lấy hết sỏi trong lượt bốc đầu tiên.
Với $n = 4$, An không thể lấy hết sỏi trong lần bốc đầu tiên vì số sỏi được lấy tối đa mỗi lần chỉ là $3$. Nếu Bình là một người thông minh và luôn biết được những nước đi tối ưu, An sẽ luôn thua do:
- Nếu An chọn lấy $1$ viên, số sỏi còn lại là $n' = 3$, lúc đó Bình có thể dùng chiến thuật của An ở trên, đó là lấy hết sỏi để chiến thắng.
- Tương tự, nếu An chọn lấy $2$ hoặc $3$ viên thì bạn cũng sẽ thua.
Do đó, trong trường hợp này An nên cố gắng kéo dài trò chơi bằng cách chỉ bốc $1$ viên sỏi và hi vọng Bình sẽ phạm sai lầm. Tuy nhiên như đã nói, nếu Bình là một người chơi có chiến thuật tối ưu thì An sẽ luôn thua. Từ trường hợp này, ta thấy trường hợp $n = 4$ là một trường hợp "xấu" do nó đặt người ở lượt đi hiện tại vào thế bất lợi.
Từ nhận xét trên, ta thấy nếu $n = 5,6,7$, An luôn có thể thắng bằng cách lấy sỏi sao cho số sỏi còn lại là $n'=4$, mục đích là để ép Bình vào trường hợp bất lợi (cũng là có lợi cho An).
Ta rút ra được một quy luật của trò chơi: nếu ở lượt của ai mà số sỏi là $4, 8, 12,\ldots$ hay nói cách khác $n$ chia hết cho $4$ thì người đó sẽ ở vị trí bất lợi.
Vậy chiến thuật tối ưu của An dựa trên số sỏi hiện tại $m$ sẽ là:$(x, x - c)$
- Nếu $m \bmod 4 \neq 0$ thì An sẽ bốc $m \bmod 4$ viên sỏi để ép Bình vào trường hợp bất lợi $m' \bmod 4 = 0$.
- Nếu $m \bmod 4 = 0$ thì An sẽ bốc $1$ viên sỏi để kéo dài trò chơi và chờ sai lầm của Bình.
với $\bmod$ là phép lấy phần dư.
Trò chơi tổ hợp cân bằng
Trò chơi ở trên chính là một ví dụ điển hình cho trò chơi tổ hợp cân bằng. Trong phần này, chúng ta sẽ tổng quát hóa bài toán này thành định nghĩa trò chơi tổ hợp cân bằng để thể giải được một lớp bài toán lớn hơn.
Định nghĩa
Trò chơi tổ hợp là trò chơi gồm: hai người chơi (ở đây gọi người chơi trước là $A$ và người chơi sau là $B$), một tập hữu hạn các trạng thái $S$ (viết tắt của State) có thể đạt được của trò chơi. Mỗi người chơi có một tập các bước di chuyển hợp lệ $Q$ để di chuyển từ trạng thái này sang trạng thái khác (gọi là luật chơi) và một tập các trạng thái kết thúc gọi là $T \subset S$ (viết tắt của Terminal). Hai người chơi sẽ luân phiên di chuyển từ trạng thái này sang trạng thái khác. Người đến được trạng thái kết thúc trước sẽ là người chiến thắng.
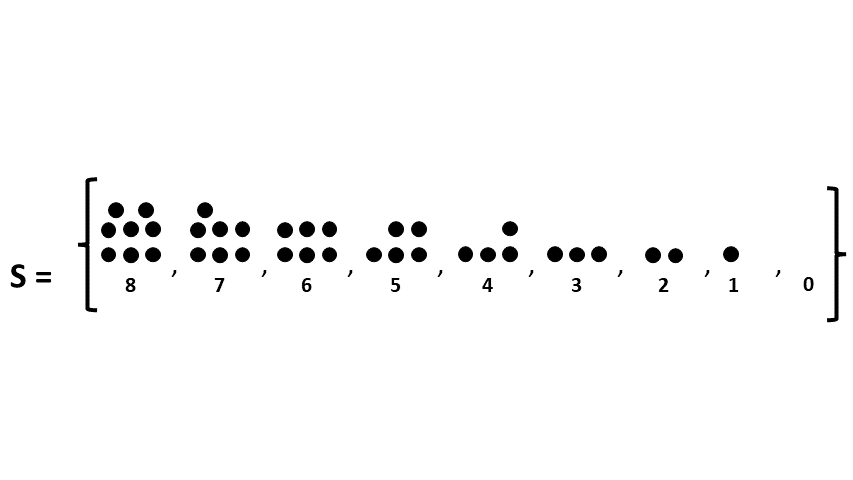
Trong trò chơi ví dụ, giả sử $n = 8$ thì mỗi trạng thái sẽ là số sỏi còn lại hiện tại của trò chơi. Do đó tập trạng thái của trò chơi là $S = {0,1,\ldots, 8}$ (hình dưới).
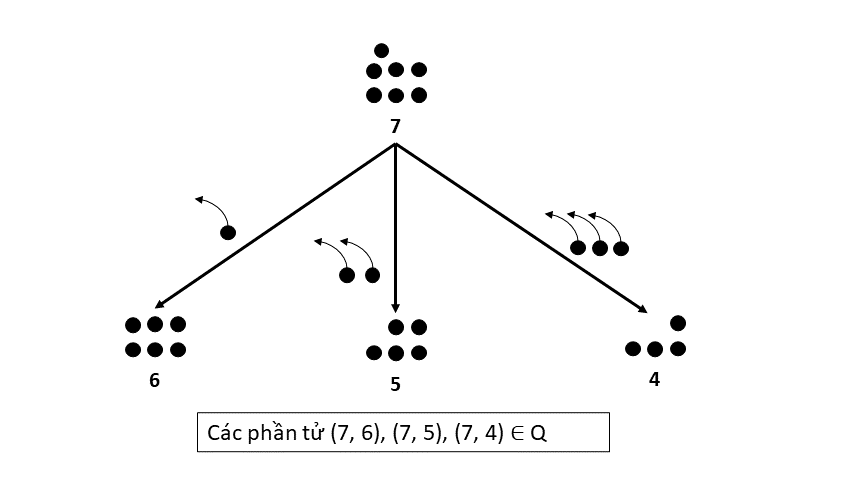
Giả sử đang ở trạng thái $x = 7$, ta có thể di chuyển hợp lệ đến trạng thái $x' = 6$ (lấy ra $1$ viên sỏi), $x' = 5$ (lấy ra $2$ viên sỏi) hoặc $x' = 4$ (lấy ra $3$ viên sỏi). Do đó ta có các phần tử $(7, 6), (7,5), (7,4)$ thuộc tập di chuyển hợp lệ $Q$ (hình dưới).
Từ đó, ta nhận xét được tập các bước di chuyển hợp lệ $Q$ của cả hai người chơi sẽ là tất cả những cặp số nguyên $(x,x - c)$ ($0 \leq x \leq n$) sao cho $c \in {1, 2, 3}$ (từ trạng thái có số sỏi $x$ chỉ có thể lấy ra $1$, $2$, hoặc $3$ viên sỏi) và $x - c \geq 0$ (số sỏi lấy ra không được phép lớn hơn số sỏi đang có).
Trò chơi kết thúc khi không còn viên sỏi nào để bốc, do đó tập trạng thái kết thúc của cả hai người chơi là $T = {0}$. Khi đó người bốc viên sỏi cuối cùng sẽ là người thắng.
Khi hai người chơi có tập các bước di chuyển hợp lệ $Q$ và tập trạng thái kết thúc $T$ giống nhau thì trò chơi được gọi là trò chơi tổ hợp cân bằng. Nói cách khác, hai người chơi chỉ khác nhau ở đúng một điểm là người này được đi trước, người kia đi sau.
Trò chơi bốc sỏi ở ví dụ chính là một trò chơi tổ hợp cân bằng, do cả An và Bình đều chỉ được cho phép bốc $1$, $2$, hoặc $3$ viên sỏi một lần và đều thắng khi bốc được viên sỏi cuối cùng.
Chiến thuật thắng
Mục tiêu của chúng ta khi giải các bài toán với trò chơi tổ hợp cân bằng là tìm ra chiến thuật mà ở đó một trong hai người chơi luôn có thể ép người còn lại thua. Chiến thuật như vậy gọi là một chiến thuật thắng.
Rõ ràng khi phân tích trò chơi bốc sỏi, ta thấy rằng nếu cả An và Bình đều chơi tối ưu thì chỉ cần biết được trạng thái ban đầu của trò chơi, ta có thể xác định được người đi trước (An) sẽ thắng hay thua. Nếu số sỏi ban đầu là $n$ chia hết cho $4$, Bình chắc chắn sẽ thắng do bạn sẽ luôn ép An đi tới trạng thái có $n$ chia hết cho $4$ và cuối cùng là $n = 0$ (cũng chia hết cho $4$). Lập luận tương tự, nếu $n$ không chia hết cho $4$ thì chắc chắn An sẽ thắng.
Vậy từ đây, ta thấy với một trò chơi tổ hợp cân bằng, chỉ cần biết trạng thái ban đầu, ta có thể suy ra được ai sẽ là người chiến thắng. Để phục vụ cho việc đưa ra chiến thuật thắng, người ta phân loại các trạng thái cùa trò chơi thành 2 tập $N$ và $P$:
- $N$: tập các trạng thái $x \in S$ sao cho nếu trạng thái ban đầu của trò chơi là $x$ thì người chơi trước luôn chiến thắng.
- $P$: tập các trạng thái $x \in S$ sao cho nếu trạng thái ban đầu của trò chơi là $x$ thì người chơi sau luôn chiến thắng.
Trong trò chơi ví dụ, nếu số sỏi ban đầu là $n = 8$ thì
- $N = {1, 2, 3, 5, 6, 7}$
- $P = {0, 4, 8}$
Từ định nghĩa trên, $N$ và $P$ sẽ thỏa ba tính chất sau:
- Tập $P$ phải chứa toàn bộ trạng thái kết thúc.
- Với mỗi trạng thái $s$ thuộc tập $N$, tồn tại ít nhất một trạng thái $s'$ đến được từ $s$ mà thuộc tập $P$.
- Với mỗi trạng thái $s$ thuộc tập $P$, tất cả các trạng thái $s'$ đến được từ $s$ phải thuộc tập $N$.
Tới đây, có thể bạn sẽ đặt ra câu hỏi: Liệu mọi trạng thái của trò chơi đều thuộc một trong hai tập $N$ hay $P$? Ta có thể chứng minh dễ dàng bằng quy nạp mạnh theo số bước tối đa để đạt tới trạng thái kết thúc. Nếu muốn, bạn đọc có thể tham khảo thêm ở phần 1.1. Impartial game - Game Theory, Alive.
Ràng buộc đầu tiên xác định trường hợp cơ bản nhất. Hai ràng buộc sau sẽ giúp chúng ta liên tục đệ quy từ trường hợp cơ bản để xây dựng được tập $P$ và $N$ hoàn chỉnh. Ta sẽ thấy rõ điều này ở phần Thuật toán xác định tập $P$ và $N$.
Khi xây dựng được tập $P$ và $N$ theo các ràng buộc trên, ta có thể dễ dàng xây dựng chiến thuật thắng cho người chơi $A$ như sau (do đây là trò chơi tổ hợp cân bằng nên chiến thuật thắng của $B$ cũng sẽ tương tự):
- Nếu $A$ bắt đầu ở trạng thái thuộc $N$, luôn đi tới trạng thái thuộc $P$ để ép $B$ đi vào trạng thái thuộc $N$. Do người thắng là người đi vào trạng thái kết thúc, mà trạng thái kết thúc lại thuộc $P$ nên chắc chắn $A$ sẽ thắng.
- Nếu $A$ bắt đầu ở trạng thái thuộc $P$, $A$ chỉ có thể kéo dài ván đấu và đợi sơ hở của $B$ ($B$ đi vào vị trí thuộc $N$) và dùng chiến thuật thắng ở trường hợp đầu. Tuy nhiên nếu $B$ cũng chơi tối ưu thì chắc chắn $A$ sẽ thua.
Qua đó, ta thấy được ý nghĩa của việc đặt tên tập $P$ và $N$. $P$ là viết tắt của positive, đặt tên như vậy vì người nào đi đến trạng thái này sẽ có lợi, đó là lý do tại sao các trạng thái kết thúc lại thuộc $P$, vì người chơi nào đi tới được trạng thái kết thúc sẽ có lợi (thắng trò chơi). Tương tự, $N$ là viết tắt của negative, đặt tên như vậy vì người nào đi đến trạng thái thuộc tập $N$ sẽ bị bất lợi (vì người kia sẽ luôn tìm cách đi được vào trạng thái thuộc $P$).
Thuật toán xác định tập P và N
Ta có ý tưởng thuật toán để tìm tập $P$ và $N$ như sau:
// Hàm kiểm tra một trạng thái thuộc P (true) hay N (false)
bool isInP(State u) {
if (u in T) // nếu u là trạng thái kết thúc thì u thuộc P
return true;
// duyệt qua tất cả các trạng thái v trong tập hợp S
for (State v in S)
if (u, v) in Q and isInP(v)
return false; // nếu có v thuộc P thì u thuộc N
return true; // nếu không thì u thuộc P
}- Nếu trạng thái $u$ đang xét là trạng thái kết thúc thì thêm $u$ vào tập $P$. Đây chính là trường hợp cơ bản của quá trình đệ quy.
- Nếu $u$ không là trạng thái kết thúc thì đệ quy đến những trạng thái $v$ mà từ $u$ có thể di chuyển trực tiếp đến. Nếu có bất kỳ $v$ nào thuộc tập $P$ thì $u$ thuộc tập $N$, ngược lại (tất cả $v$ đều thuộc $N$) thì $u$ thuộc $P$.
Ở đây có một chú ý về cách cài đặt trên, đó là kiểu dữ liệu State là một kiểu dữ liệu tượng trưng để lưu một trạng thái của trò chơi. Trong thực tế, trạng thái hay được biểu diễn bằng một số nguyên int, tuy nhiên nhiều trường hợp trạng thái của chúng ta không ở dạng số nguyên, khi đó có một số cách các bạn có thể xem xét để lưu trạng thái như: bitmask, hashmap (unordered_map trong c++).
Tuy nhiên, thuật toán này có một nhược điểm, đó là gọi lại cùng một giá trị quá nhiều lần do không lưu lại kết quả trong quá trình đệ quy. Cách giải quyết chính là quy hoạch động top-down (hay còn gọi là đệ quy có nhớ), trong đó ta có một mảng $dp$ lưu lại kết quả của những trạng thái đã từng xét. Để hiểu thêm, bạn hãy xem cài đặt tìm trò chơi bốc sỏi ở phần ví dụ sau.
Ví dụ cài đặt thuật toán cho trò chơi bốc sỏi
Đầu tiên, ta cần thêm các thư viện cần thiết, cũng như khai báo mảng $dp$ để nhớ kết quả của những trạng thái đã đệ quy.
#include<bits/stdc++.h>
using namespace std;
const int MAX_N = 100000; // số trạng thái tối đa
int dp[MAX_N];Sau đó, ta viết hàm xác định xem trạng thái $u$ có thuộc $P$ không như sau
bool isInP(int u) {
if (dp[u] != -1) // nếu u đã được tính trước đó thì
return dp[u];
if (u == 0) { // u = 0 là trạng thái kết thúc nên thuộc P
dp[u] = 1;
return 1;
}
// Từ u chỉ có thể đi tới các v hợp lệ
for (int v = u - 1; v >= max(u - 3, 0); v--)
if (isInP(v)) {
dp[u] = 0;
return false;
}
// u không đi được trạng thái nào thuộc P
dp[u] = 1;
return true;
}Ở đây quy ước giá trị của mảng $dp$ như sau:
- $dp[u] = 0$ nghĩa là trạng thái $u$ đã xét và $u$ không thuộc $P$, hay nói cách khác $u$ thuộc $N$.
- $dp[u] = 1$ nghĩa là trạng thái $u$ đã xét và $u$ thuộc $P$.
- $dp[u] = -1$ nghĩa là trạng thái $u$ chưa xét.
Sở dĩ ta quy ước như vậy vì c++ có cơ chế implicit casting. Nói đơn giản, khi trả về $dp[u]$ trong hàm isInP(u), $dp[u]$ sẽ được tự động ép kiểu về bool với quy tắc: $0$ là $\texttt{false}$, các giá trị khác là $\texttt{true}$.
Cài đặt này tối ưu thời gian đệ quy bằng hai ý sau:
- Khi tính xong, trước khi trả về giá trị thì ta lưu giá trị lại vào một mảng $dp$ và ở đầu hàm $isInP(u)$
- Ta trả về $dp[u]$ nếu $dp[u] \neq -1$ (tức $u$ đã được tính trước đó).
Cuối cùng, ta viết hàm main để nhập xuất và kết luận nghiệm. Lưu ý trước khi thực hiện quá trình tìm tập $P$ và $N$ ta phải khởi tạo mảng $dp$ thành toàn $-1$ bằng hàm fill do thư viện chuẩn của c++ cung cấp.
int main() {
int n;
cin >> n;
fill(dp, dp + n + 1, -1);
if (!isInP(n)) cout << "A win";
else cout << "B win";
return 0;
}Trò chơi Nim chuẩn
Sau khi đã tìm hiểu lý thuyết trò chơi tổ hợp cân bằng tổng quát, phần tiếp theo ta sẽ áp dụng lý thuyết đó vào một bài toán kinh điển trong lý thuyết trò chơi - trò chơi Nim - đại diện tiêu biểu cho trò chơi tổ hợp cân bằng.
Phát biểu trò chơi
Có $n$ đống sỏi, và mỗi đống lần lượt có $p_1, p_2, \ldots, p_n$ sỏi, trong đó mỗi số $p_i$ là một số nguyên không âm. Mỗi trạng thái trò chơi tương ứng với mỗi bộ $n$ cho biết số sỏi của từng đống này.
Có hai người chơi thay phiên nhau bỏ sỏi. Người chơi trong lượt hiện tại có thể loại bỏ bao nhiêu sỏi tùy thích, miễn là tất cả các sỏi đều cùng một đống. Hình thức hơn, người chơi sẽ chọn một đống sỏi $i$ và số lượng sỏi $s$ để loại bỏ khỏi đống ($0 < s \leq p_i$), sau đó thay $p_i$ bằng $p_i-s$. Chú ý rằng người chơi không thể bỏ qua lượt của mình mà không bỏ viên sỏi nào cả. Sau đó, đến lượt người chơi kia loại bỏ sỏi, lần lượt như vậy tới khi trò chơi kết thúc.
Trò chơi kết thúc khi không còn sỏi trên bàn chơi. Người chiến thắng là người lấy được viên sỏi cuối cùng. Nói cách khác, người thua cuộc là người đầu tiên không thể lấy sỏi trong lượt của mình.
Trò bốc sỏi ở ví dụ trên chính là biến thể của trò chơi Nim chuẩn, khác hai chỗ là ở đây chỉ có một đống sỏi ($n = 1$) và số sỏi lấy ra tối đa ở mỗi đống là $3$.
Giá trị Nim
Mục tiêu lớn nhất của chúng ta vẫn là xác định xem ai là người thắng nếu cả hai người chơi tối ưu, hay nói cách khác là xác định được chiến thuật thắng.
Tuy nhiên, khi bắt tay vào làm, bạn sẽ gặp ngay một rào cản, đó là trạng thái của trò chơi đang được biểu diễn dưới dạng một bộ các số nguyên chứ không phải một số nguyên, điều đó gây khó khăn cho chúng ta khi tổng quát hóa lời giải và lập trình, một khó khăn rất dễ thấy đó là nếu chúng ta xài mảng $dp$ nhiều chiều để lưu trạng thái đã tính thì có khả năng khi $n$ thay đổi đoạn code cũ sẽ không dùng được nữa do số chiều của mảng đã thay đổi. Theo suy nghĩ tự nhiên, chúng ta sẽ cố gắng tìm cách kết hợp thông tin của bộ trạng thái $n$ số lại thành một số nguyên duy nhất. Một cách khả thi để làm điều này chính là giá trị Nim, ký hiệu là $g$.
Đầu tiên, hãy giải quyết trường hợp đơn giản nhất - chỉ có một đống sỏi duy nhất với $p$ viên sỏi.
- Theo trực giác, vì thông tin duy nhất ta có là số lượng sỏi trong đống, ta có thể giả sử rằng giá trị Nim của trường hợp này là một số nguyên $p$ cho biết số sỏi còn lại.
- Chúng ta thấy rằng nếu $p > 0$ thì trạng thái trò chơi hiện tại thuộc $N$, ngược lại nếu $p = 0$ thì trạng thái trò chơi hiện tại thuộc $P$. Điều này có thể giải thích bằng việc nếu số sỏi là số dương, người đi trước luôn có thể lấy hết sỏi nên người đi sau luôn thua. Từ trường hợp đơn giản này, ta mường tượng được điều mà giá trị Nim $g$ phản ánh: trạng thái trò chơi hiện tại thuộc $N$ khi giá trị Nim dương và thuộc $P$ khi giá trị Nim bằng $0$.
Tiếp theo, chúng ta sẽ tìm cách ghép các đống sỏi đơn lại thành một trò chơi hoàn chỉnh gồm $n$ đống sỏi. Cụ thể hơn, ta sẽ tìm ra một phép toán $A \oplus B$ để biết được giá trị Nim của trò chơi mới khi kết hợp hai trò chơi có giá trị Nim lần lượt là $A$ và $B$ lại. Ta sẽ liệt kê một số tính chất cần có của phép toán này để có thể gộp các giá trị của cột lại:
- $(A \oplus B) \oplus C = A \oplus (B \oplus C)$, và $A \oplus B = B \oplus A$, nghĩa là $\oplus$ có tính chất kết hợp và giao hoán. Tính chất này có thể giải thích bằng lập luận rằng thứ tự các cọc không thực sự quan trọng nên khi đổi thứ tự kết hợp thì giá trị Nim không thay đổi.
- $A \oplus 0 = A$, nghĩa là, phần tử trung hòa của toán tử này là $0$. Điều này rất hiển nhiên vì nếu bạn thêm một đống sỏi trống vào trò chơi, thì trò chơi vẫn không thay đổi, do đó giá trị Nim vẫn như cũ.
- $A \oplus A = 0$, nghĩa là phần tử đối của mỗi trạng thái trò chơi là chính nó. Tại sao điều này lại đúng? Giả sử chúng ta có hai đống sỏi giống nhau, mỗi đống có $p$ viên sỏi. Lúc đó, người đi sau luôn có một chiến lược chiến thắng, đó là chỉ sao chép bước đi của người đi trước! Điều tương tự xảy ra với trường hợp tổng quát. Do đó, người đi trước sẽ luôn là người thua, tức trạng thái trò chơi thuộc $P$, như ta đã lập luận ở ví dụ trước, trạng thái thuộc $P$ tương ứng với $g = 0$, do đó $A \oplus A = 0$.
Ba thuộc tính này, đặc biệt nhất là tính chất $A \oplus A = 0$ giúp chúng ta tìm ra một ứng cử viên tìm năng, đó là phép bitwise XOR. Và quả thật phép toán này cũng chính là đáp án chúng ta cần tìm, định lý Bouton được trình bày ở phía dưới sẽ chứng minh tính đúng đắn của việc này.
Thực chất, phép bitwise XOR chỉ là phép cộng modulo $2$ trên từng bit, do đó chúng ta hay gọi giá trị Nim là tổng Nim. Tổng Nim của một trò chơi có trạng thái $(p_1, p_2, \ldots, p_n)$ thu được bằng cách thực hiện phép XOR các $p_i$ lại với nhau. $g = p_1 \oplus p_2 \oplus \ldots \oplus p_n$
Ví dụ: với trò chơi Nim có ba đống sỏi với số sỏi lần lượt là $5$, $7$, $3$ thì tổng Nim là $0101 \oplus 0111 \oplus 0011 = 0001$.
Định lý Bouton
Tuy nhiên, trong phần trình bày ở phía trên có một giả thuyết rất quan trọng mà ta chỉ mới thừa nhận chứ chưa chứng minh, đó là trạng thái trò chơi hiện tại thuộc $N$ khi giá trị Nim dương và thuộc $P$ khi giá trị Nim bằng $0$. Thực ra, nhận xét đó là một định lý đã được chứng minh, gọi là định lý Bouton. Phần này khuyến khích bạn đọc hiểu về các tính chất của phép toán bitwise XOR.
Định lý Bouton: trạng thái của trò chơi Nim $(p_1, p_2, \ldots, p_n)$ thuộc $P$ khi và chỉ khi tổng Nim $g$ của nó bằng $0$.
Chứng minh
Gọi $\hat{P}$ là tập gồm các trạng thái có tổng Nim bằng $0$ và $\hat{N}$ là tập gồm các trạng thái có tổng Nim lớn hơn $0$. Ta nhận xét hai tập này có các tính chất sau:
Đầu tiên, trạng thái kết thúc là $(0,\ldots,0)$ thuộc $\hat{P}$ do có tổng Nim là $0$
Thứ hai, với một trạng thái thuộc $\hat{N}$ ($g > 0$), ta luôn có thể đi tới một trạng thái thuộc $\hat{P}$ ($g = 0$). Để chứng minh, chọn một đống sỏi thứ $i$ có $p_i$ sỏi và biến nó thành $p'_i$ sao cho $p'_i = g \oplus p_i < p_i$, ta có được tổng Nim mới $g'$ như sau:
Lưu ý rằng phép XOR không giống phép cộng thông thường. Ở phép cộng hai số nguyên dương, kết quả luôn lớn hơn các toán hạng ban đầu. Tuy nhiên, trong phép XOR điều này không xảy ra, kết quả có thể lớn hơn hoặc nhỏ hơn các toán hạng ban đầu. Do đó việc ta có thể đảm bảo luôn tồn tại đống sỏi $i$ thỏa mãn yêu cầu $p'_i = g \oplus p_i < p_i$ không phải là điều hiển nhiên và cần được chứng minh.
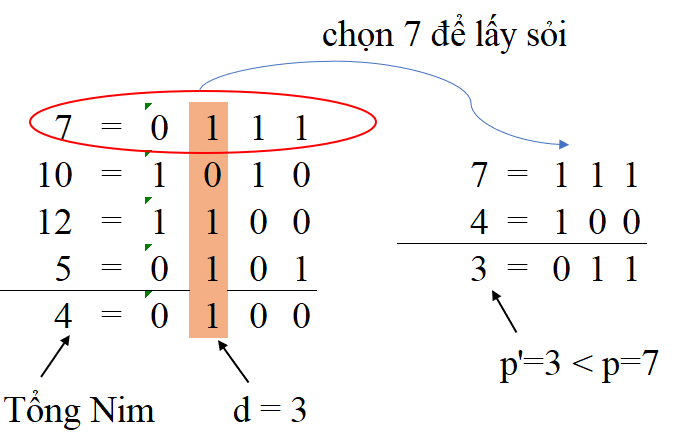
Vì $g > 0$ nên biểu diễn nhị phân của $g$ luôn tồn tại bit trái nhất bằng $1$ (tạm gọi là $d$).Khi đó, xét bit thứ $d$ của tất cả các cột $p_i$, ta có số lượng $p_i$ có bit thứ $d$ bằng $1$ phải lẻ (theo tính chất của phép XOR), do đó luôn tồn tại một đống sỏi có bit thứ $d$ bằng $1$. Chọn đống sỏi có bit thứ $d$ bằng $1$ đó để thực hiện bốc sỏi, ta thấy $p'_i = p_i \oplus g < p_i$ bởi vì khi XOR bit tại vị trí $d$ bằng $1 \oplus 1 = 0$, do đó $p'_i$ luôn mất một bit $1$ tại vị trí $d$ so với $p_i$.
Ví dụ, nếu trò chơi Nim hiện tại có $4$ cột có số sỏi lần lượt là $7$, $10$, $12$, $5$, thì thao tác tính tổng Nim và chọn cột để lấy sỏi ra sẽ diễn ra như hình dưới
Cuối cùng, với một trạng thái thuộc $\hat{P}$ (tức $g = 0$), mọi cách đi đều dẫn tới trạng thái thuộc $\hat{N}$ (tức $g > 0$). Ta có thể chứng minh dễ dàng bằng phương pháp phản chứng. Giả sử trạng thái trò chơi hiện tại là $(p_1, \ldots, p_n)$ có tổng Nim $g = 0$ và tồn tại một đống sỏi $i$ sao cho khi lấy bớt sỏi từ $i$ ra trạng thái trò chơi mới có tổng Nim $g' = 0$. Khi đó
Điều này có nghĩa là ta không bốc viên sỏi nào từ đống $p_i$ ra cả, mà theo giả thuyết ta phải bốc ít nhất một viên ($p'_i < p_i$), vì vậy không thể tồn tại đống sỏi $i$ nào thỏa mãn yêu cầu.
Ví dụ, nếu trò chơi Nim hiện tại có $3$ đống có số sỏi lần lượt là $5$, $6$, $3$, thì tổng Nim $g = 0$. Xét bit đầu tiên từ phải qua, ta thấy được số lượng bit được bật tại vị trí này là số chẵn ($2$, tương ứng với bit đầu tiên của $5$ và $3$). Tương tự, số lượng các bit được bật tại các vị trị khác đều có tính chất này. Điều này không phải là trùng hợp mà do tính chất của phép XOR, nếu muốn bit thứ $i$ trong kết quả bằng $0$ thì số lượng bit thứ $i$ được bật trong các toán hạng phải là số chẵn. Từ đây ta nhận thấy, việc bỏ sỏi ở một đống sỏi chỉ có thể làm thay đổi số lượng bit được bật tại mỗi vị trí $i$ lên hoặc xuống 1 đơn vị, do đó dù cho lấy sỏi ở cột nào đi nữa thì vẫn sẽ xuất hiện một vị trí có số bit được bật là lẻ.
Rõ ràng $\hat{P}$ và $\hat{N}$ thỏa mãn ba điều kiện theo định nghĩa của tập $P$ và $N$ trong trò chơi tổng quát, vì vậy $P = \hat{P}$ và $N = \hat{N}$. $\square$
Qua định lý Bouton, chúng ta có một cách xác định tập $P$ và $N$ dựa trên tổng Nim, hơn thế nữa với việc chứng minh định lý Bouton, ta không chỉ biết được trạng thái thắng/thua của trò chơi mà còn có thể xây dựng được một chiến thuật thắng cụ thể.
Cài đặt
Hàm isInP trong trường hợp này rất đơn giản, nếu lưu số lượng sỏi mỗi đống vào vector số nguyên thì thuật toán chỉ đơn giản là XOR của các phần tử với nhau, độ phức tạp thuật toán là $O(n)$.
bool isInP(vector<int> v) {
int g = 0;
for (auto p: v)
g ^= p;
return (g == 0);
}Misère Nim
Ngoài trò chơi Nim chuẩn, có rất nhiều biến thể của trò chơi Nim. Một trong số đó là misère Nim, cách chơi giống như trò chơi Nim bình thường, tuy nhiên thay vì người lấy viên sỏi cuối cùng sẽ thắng, trong Misère Nim thì người lấy viên sỏi cuối cùng sẽ thua.
Khi đó, dựa vào trạng thái bắt đầu, ta có thể xác định việc thắng thua như sau:
- Nếu tất cả đống sỏi đều có số sỏi nhỏ hơn hơn $2$ (tức chỉ gồm các đống sỏi có $0$ và $1$ viên): nếu số lượng đống sỏi còn sỏi là lẻ (tức giá trị Nim $g=1$) thì người chơi đầu tiên sẽ thua, ngược lại (tức $g=0$) thì người chơi đầu tiên sẽ thắng.
- Các trường hợp còn lại: Người chơi đầu tiên sẽ thắng nếu giá trị Nim hiện tại $g > 0$ , ngược lại sẽ thua. Chiến thuật để giành chiến thắng là chơi theo chiến lược Nim thông thường, trừ khi bước di chuyển tiếp theo làm các đống sỏi đều có nhỏ hơn $2$ viên, lúc đó người chơi thực hiện nước đi hiện tại sẽ đặt số lượng đống có $1$ viên sỏi là số lẻ để ép người kia phải bốc viên cuối cùng. Ta có thể chứng minh được nếu một người đang ở trạng thái có giá trị Nim $g > 0$, anh ta luôn có thể quyết định số lượng đống sỏi là chẵn hay lẻ và do đó luôn là người chiến thắng.
Định lý Sprague-Grundy
Đồ thị của trò chơi
Nếu xem mỗi trạng thái trong tập trạng thái $S$ là một đỉnh, mỗi cạnh có hướng $(u,v)$ thể hiện cho việc từ trạng $u$ có thể di chuyển đến trạng thái $v$ (tức $(u,v)$ là một phần tử thuộc tập các bước di chuyển di chuyển hợp lệ $Q$) thì ta có thể xây dựng một đồ thị có hướng $(V,E)$ với tập đỉnh $V$ và tập cạnh $E$ tương ứng với tập trạng thái $S$ và tập các bước di chuyển $Q$ như đã nói. Ở đây có một quan sát quan trọng rằng ta tất cả các trạng thái kết thúc sẽ ứng với những đỉnh những đỉnh có bậc ra bằng $0$ (tức từ đỉnh này không đi tới được bất kỳ đỉnh nào khác)
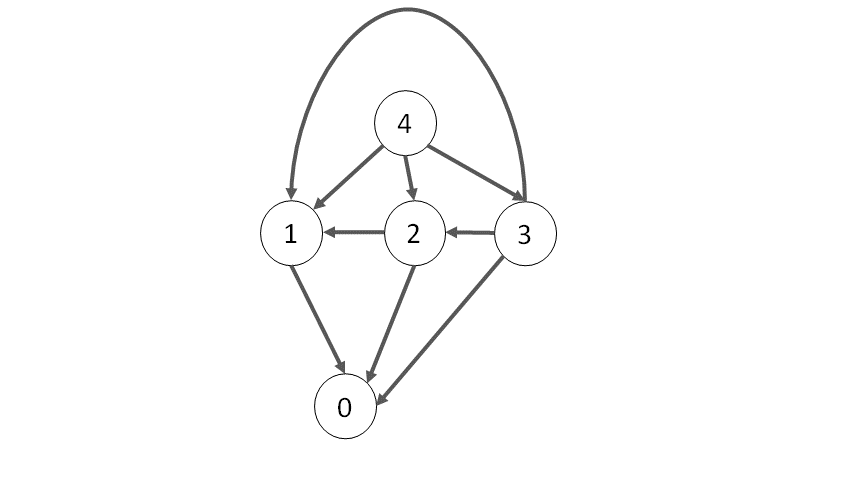
Ví dụ: trong trò chơi bốc sỏi ở phần đầu, giả sử ta chỉ có một đống sỏi $4$ viên, thì đồ thị của trò chơi sẽ như hình dưới, trạng thái kết thúc $0$ có bậc ra bằng $0$.
Cũng cần chú ý rằng các trò chơi được xem xét trong phần định lý Sprague-Grundy có một tính chất quan trọng, đó là chúng sẽ kết thúc trong hữu hạn bước. Khi đó, hiển nhiên đồ thị trò chơi phải không tồn tại chu trình, vì nếu tồn tại chu trình, sẽ tồn tại trường hợp người chơi cố tình đi theo chu trình đó và sẽ không bao giờ đến được đỉnh kết thúc, nghĩa là khi đó trò chơi sẽ lặp vĩnh viễn. Loại đồ thị có hướng không có chu trình như trên còn có thể gọi tắt là DAG (Directed Acyclic Graph).
Trò chơi tổng
Để có thể kết hợp nhiều trò chơi đơn lẻ với nhau, ta đặt ra khái niệm trò chơi tổng.
Trò chơi tổng: Cho trò chơi $G_1(S_1,Q_1, T_1)$ và $G_2(S_2,Q_2,T_2)$ với $S_i,Q_i, T_i$ là tập trạng thái, tập các bước di chuyển hợp lệ và tập trạng thái kết thúc ứng với trò chơi $1$ và $2$, trò chơi tổng $G = G_1 + G_2$ là trò chơi có:
- Tập trạng thái $S = S_1 \times S_2$, tức trạng thái của trò chơi tổng là các cặp trạng thái $(x_1, x_2)$ với $x_1$ là trạng thái thuộc $S_1$ và $x_2$ là trạng thái thuộc $S_2$.
- Tập các bước di chuyển hợp lệ $Q = (Q_1\times {x_2}) \cup ({x_1} \times Q_2)$, nghĩa là một bước di chuyển hợp lệ trong trò chơi tổng sẽ tương ứng với việc thực hiện một bước di chuyển hợp lệ trong trò chơi con $G_1$ hoặc $G_2$ và giữ nguyên trạng thái trò chơi còn lại.
- Tập các trạng thái kết thúc $T = \{ (x_1, x_2) : x_1 \in T_1 \wedge x_2 \in T_2 \}$, nghĩa là trạng thái kết thúc của trò chơi tổng là trạng thái mà cả hai trò chơi $G_1$ và $G_2$ đều kết thúc.
Ví dụ: trò chơi Nim có $3$ đống sỏi có thể xem như trò chơi tổng của ba trò chơi $G_1$, $G_2$ và $G_3$, với $G_1$ là trò chơi chỉ bốc ở đống sỏi thứ $1$, $G_2$ là trò chơi chỉ bốc ở đống sỏi thứ $2$, $G_3$ là trò chơi chỉ bốc ở đống sỏi thứ $3$.
Mở rộng trò chơi Nim
Định lý Bouton đã cho chúng ta một cách giải rất đẹp cho trò chơi Nim chuẩn, nhưng trong thực tế, hầu hết các bài lý thuyết trò chơi trong lập trình thi đấu sẽ không là trò chơi Nim chuẩn mà sẽ được thay đổi luật chơi ở một số điểm. Lúc ấy, định lý Bouton sẽ không thể giải quyết các dạng bài này. Trong phần này, ta sẽ trình bày hai định lý quan trọng để giải quyết các trò chơi cân bằng kết thúc trong hữu hạn bước. Tuy nhiên ta sẽ chỉ trình bày về động lực hình thành và định nghĩa của hai định lý. Để hiểu rõ hơn, bạn đọc hãy đọc phần Phụ lục để hiểu được chứng minh.
Để giải quyết, ta quay lại chiến lược ban đầu của mình - phân tách trạng thái trò chơi thành nhiều trò chơi con có cùng cấu trúc, tìm một số tính chất đặc biệt của mỗi trò chơi con, sau đó kết hợp chúng lại với nhau để có câu trả lời cho trò chơi gốc.
Hãy lấy ví dụ với một biến thể của trò chơi Nim chuẩn, trong đó chúng ta có $n$ đống sỏi, luật chơi vẫn như cũ, chỉ khác là số sỏi phải bốc ở mỗi lượt phải là số chính phương ($1, 4, \ldots$).
Đầu tiên, ta cũng xét trò chơi ở dạng đơn giản nhất: chỉ có một đống sỏi duy nhất với $p$ viên. Vậy làm thế nào để bạn biết đó là trạng thái thuộc $P$ hay trạng thái thuộc $N$?
Hãy nhìn trò chơi dưới góc độ đồ thị. Đồ thị này có $p + 1$ đỉnh có nhãn lần lượt là các số nguyên từ $0$ đến $p$. Mỗi đỉnh đồ thị tương ứng với một trạng thái trò chơi, trong đó nhãn của nó cho biết có bao nhiêu sỏi còn lại trong đống hiện tại. Hình dưới là ví dụ trò chơi với một đống sỏi có số sỏi $p = 5$.
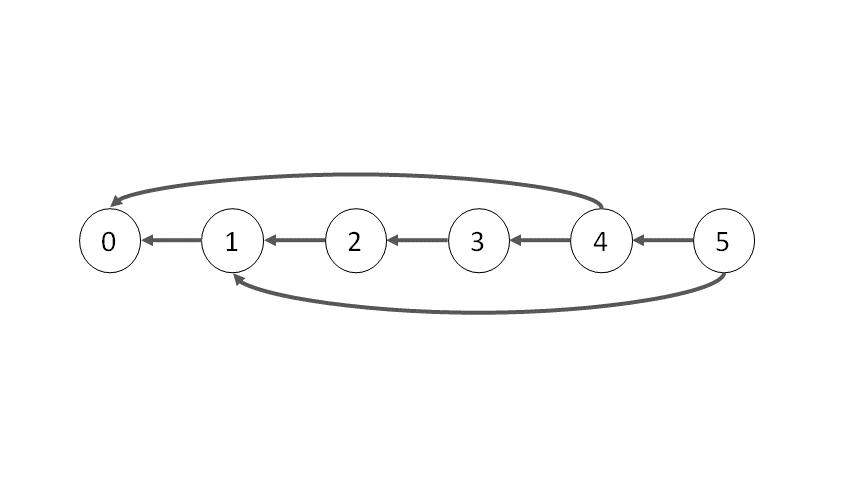
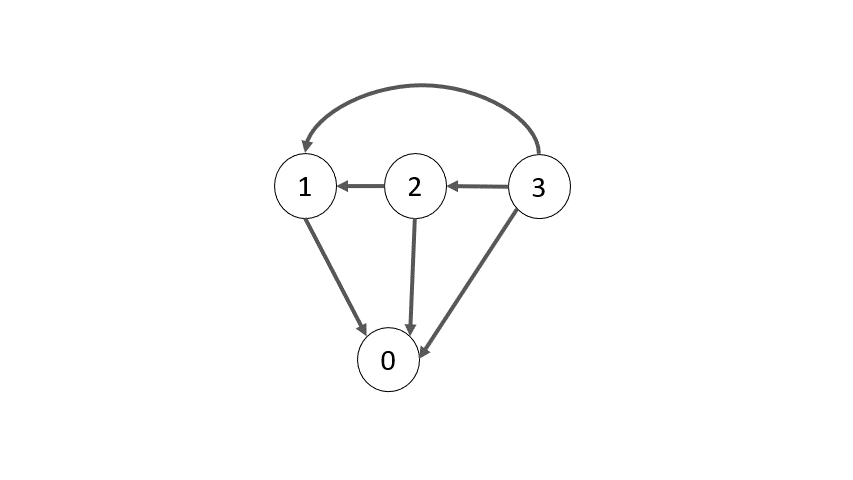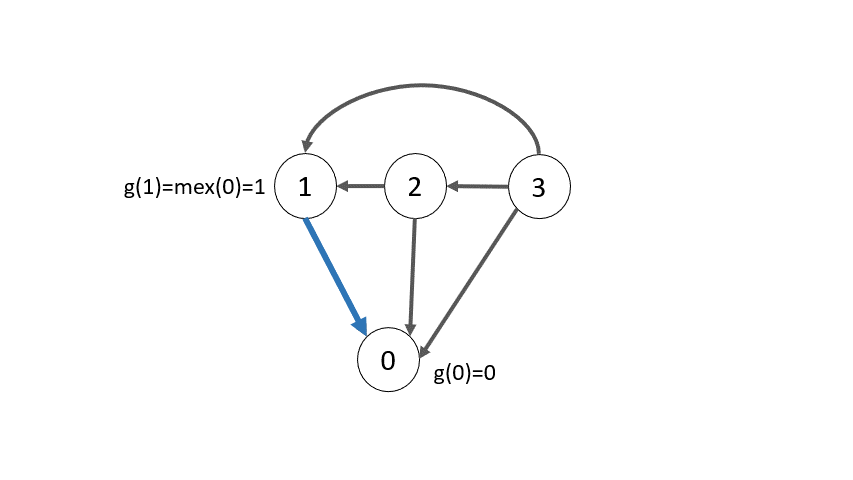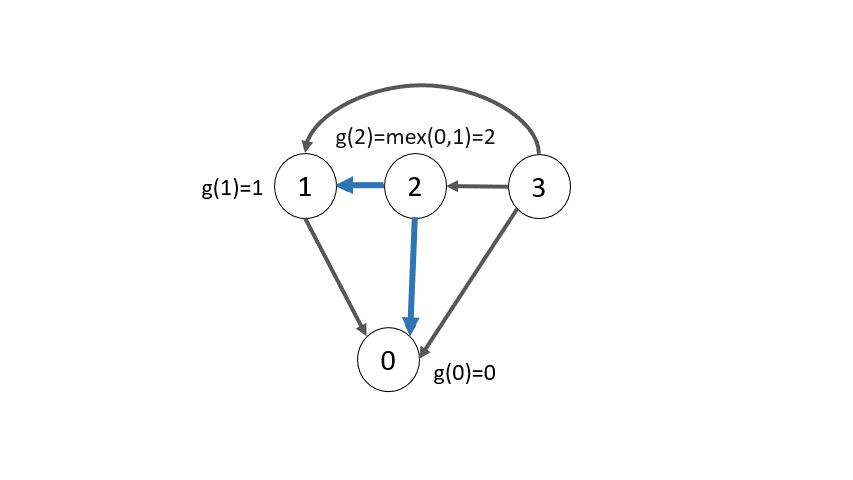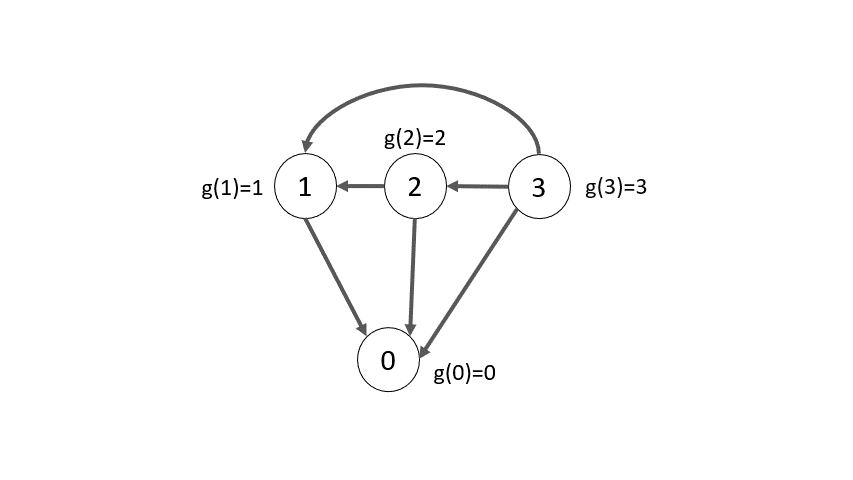
Rõ ràng đỉnh $0$ là đỉnh kết thúc, do đó nó là đỉnh thuộc $P$. Các đỉnh tiếp theo có thể xác định là thuộc $P$ hay $N$ như hình dưới
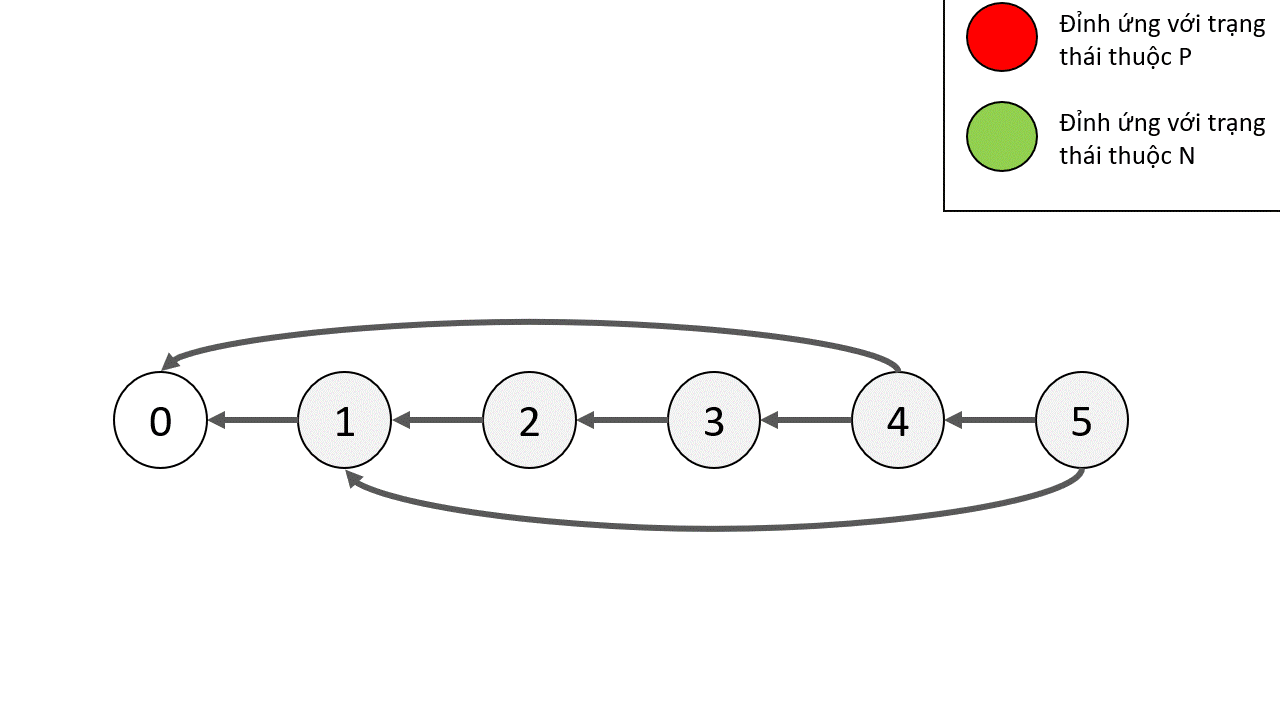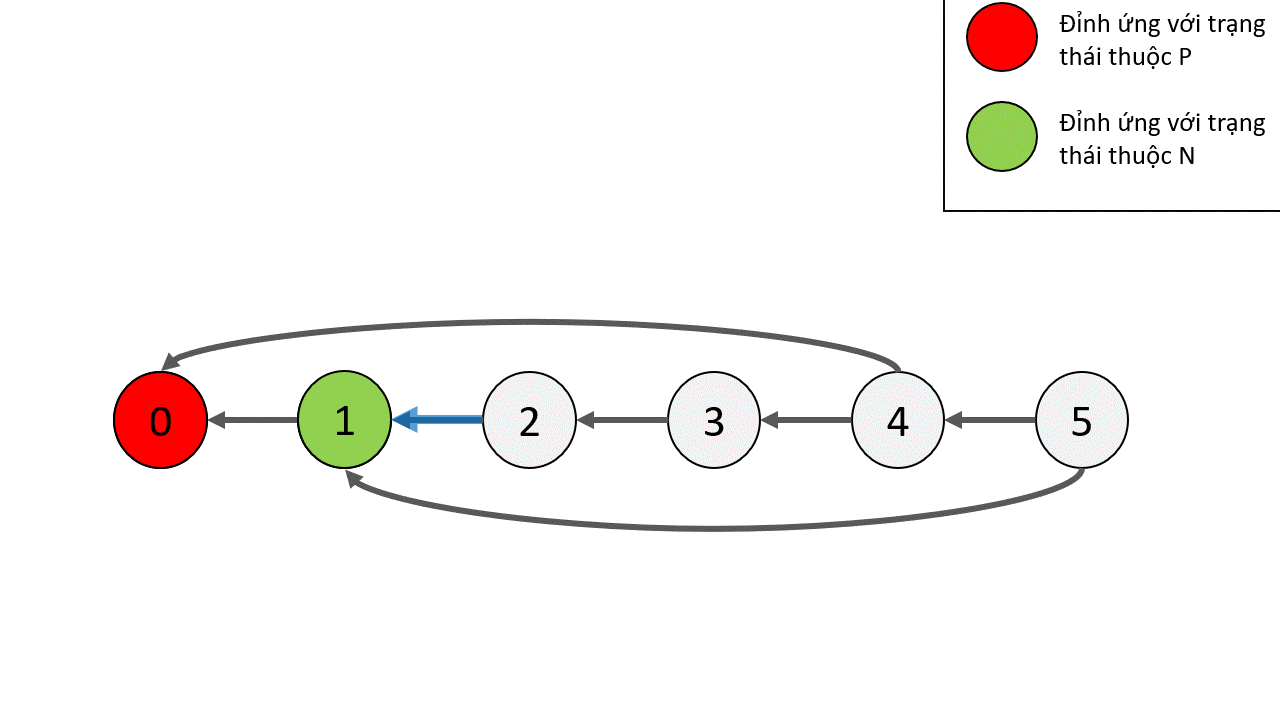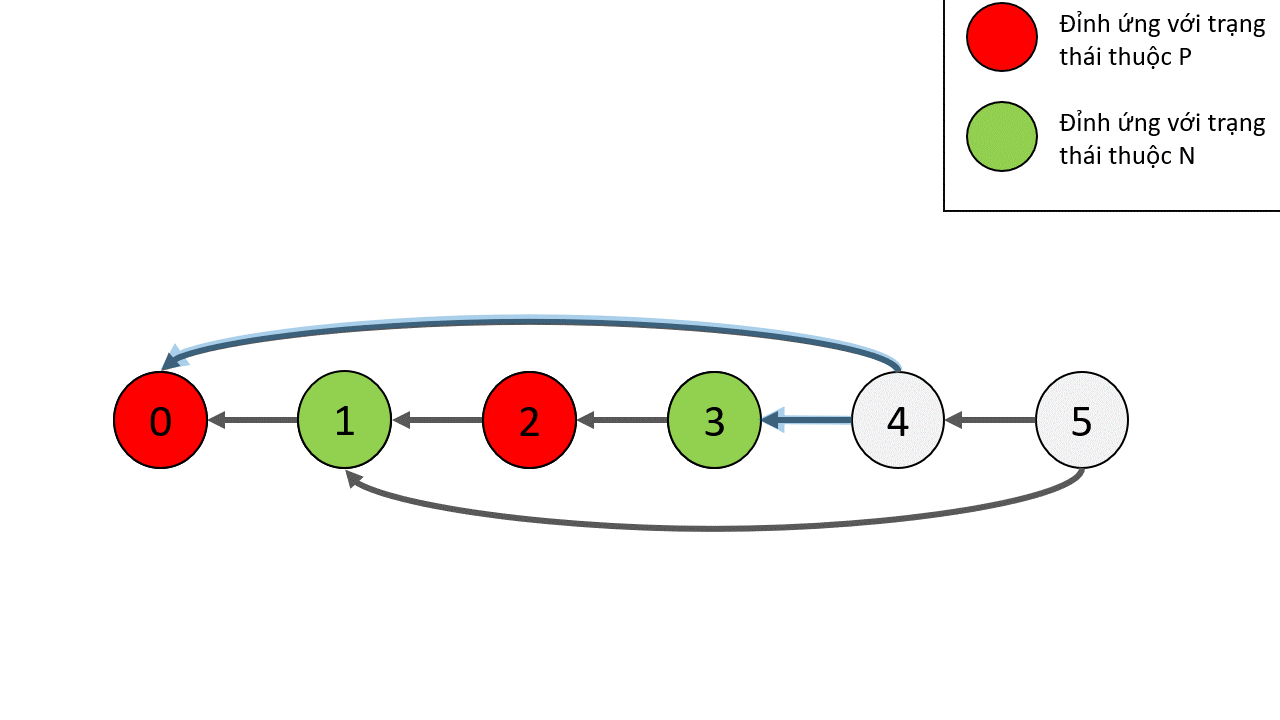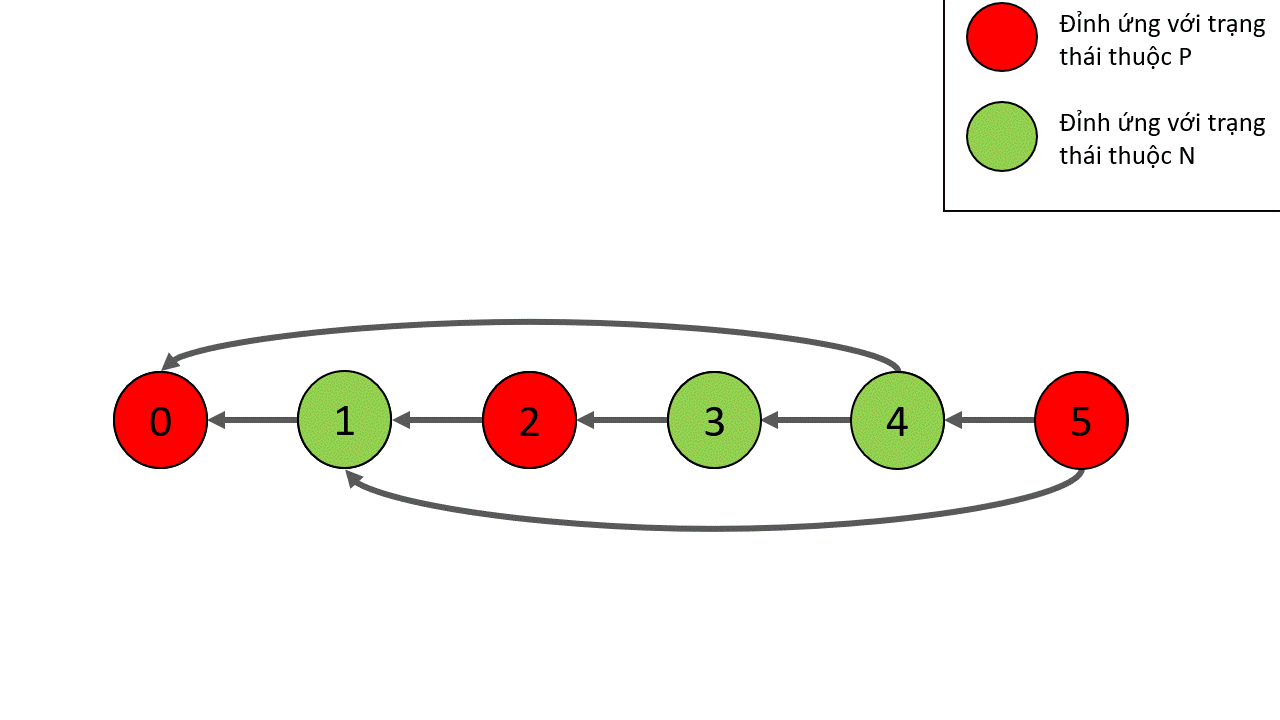
Tuy nhiên, cách làm ở trên chỉ cho ta trạng thái định tính của từng trạng thái, để phục vụ cho việc ghép các trò chơi lại, ta cần một hàm định lượng. Hàm mà chúng ta sẽ dùng có tên là hàm Sprague-Grundy, với một trạng thái $x \in S$ thì giá trị Sprague-Grundy được định nghĩa như sau: $g(x) = \text{mex}(\{g(y): (x,y) \in Q\})$
Trong định nghĩa trên có dùng hàm mex (minimum excludant), hàm này sẽ nhận vào một tập hợp và trả về số nguyên không âm $u$ nhỏ nhất sao cho $u$ không nằm trong tập hợp, ví dụ $\text{mex}({0,1,2,5,7}) = 3$. Ngoài ra, quy ước $\text{mex}(\varnothing)=0$. Từ đó, ta có thể phát biểu bằng lời rằng giá trị Sprague-Grundy của một đỉnh $x$ sẽ là mex của tập hợp các giá trị Sprague-Grundy của $y$ sao cho từ $x$ có thể di chuyển trực tiếp đến $y$.
Câu hỏi đặt ra là: tại sao lại là hàm Sprague-Grundy? Hàm này có ý nghĩa gì trong việc giải các trò chơi tổ hợp cân bằng?
Để thấy rõ hơn ý nghĩa của hàm Sprague-Grundy, ta có thể ví dụ biến thể của trò chơi Nim ở trên.
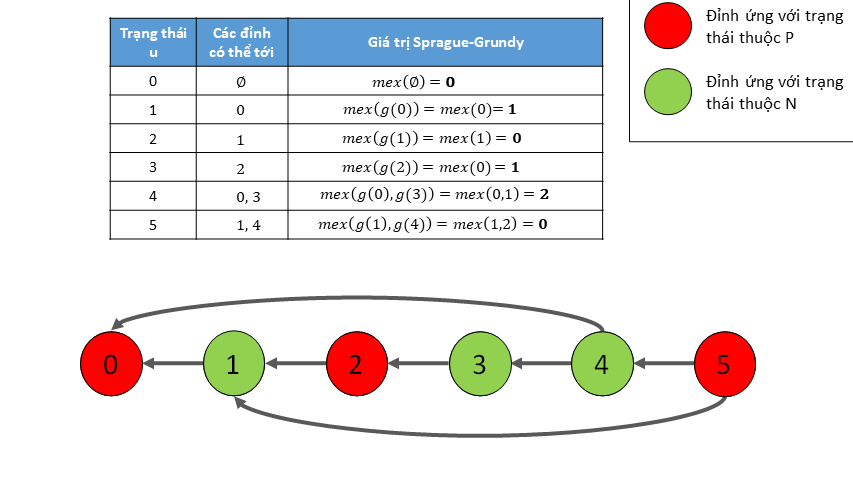
Quan sát ví dụ ở trên, ta có nhận xét rằng các trạng thái $u$ thuộc $P$ đều có $g(u) = 0$ và các trạng thái $u$ thuộc $N$ đều có $g(u) > 0$. Điều này làm ta nhận ra sự tương đồng của giá trị Sprague-Grundy với một đại lượng ở phần trước - giá trị Nim. Đó là cảm nhận ban đầu để có định lý sau.
Định lý 1: Trong một trò chơi tổ hợp cân bằng, trạng thái $u$ thuộc $P$ khi và chỉ khi giá trị Sprague-Grundy $g(u) = 0$.
Vậy với hàm Sprague-Grundy, ta đã giải quyết được trò chơi đơn giản nhất, vấn đề tiếp theo là giải trò chơi tổng. Ta cũng sẽ tìm một phép toán $\oplus$ để tìm ra giá trị Sprague-Grundy của trò chơi tổng từ hai trò chơi thành phần. Cũng như trò chơi Nim, ta sẽ thấy phép toán này có các tính chất kết hợp, giao hoán, phần tử trung hòa là $0$ và phần tử đối của một trò chơi là chính nó. Do đó, ta sẽ lại thấy phép bitwise XOR là phép toán mà chúng ta cần tìm. Tính đúng đắn của phép toán bitwise XOR được khẳng định bằng định lý sau
Định lý 2: với trò chơi tổng $G = G_1 + \ldots + G_n$ và $x_1, \ldots, x_n$ lần lượt là các trạng thái của trò chơi thành phần $G_1, \ldots, G_n$, khi đó: $g(x_1, \ldots, x_n) = g_1(x_1) \oplus \ldots \oplus g_n(x_n)$ Với $g, g_1, \ldots, g_n$ lần lượt là hàm Sprague-Grundy của trò chơi $G, G_1, \ldots, G_n$.
Ví dụ: với trò chơi Nim biến thể với luật bốc các số chính phương như trên, nhưng bây giờ ta có $3$ đống sỏi lần lượt có $5, 4, 1$ viên sỏi. Khi đó ta có thể coi mỗi đống sỏi là một trò chơi thành phần, vì vậy giá trị Sprague-Grundy của trò chơi tổng là $g(5) \oplus g(4) \oplus g(1) = 0 \oplus 2 \oplus 1 = 3$, vậy đây là trạng thái mà người chơi đi đầu tiên sẽ giành chiến thắng.
Hai định lý 1 và 2 trong phần này có ý nghĩa rất quan trọng, nó cho ta cách giải bất cứ trò chơi tổ hợp cân bằng nào, miễn là trò chơi đó luôn kết thúc trong hữu hạn bước, hay nói cách khác đồ thị của trò chơi là một DAG. Định lý 2 giúp chúng ta phân rã trò chơi phức tạp ra thành những trò chơi thành phần đơn giản hơn và định lý 1 giúp chúng ta giải quyết những trò chơi thành phần đơn giản đó.
Như vậy, ta thấy rằng thực ra cách giải trò chơi Nim cũng chỉ là một trường hợp riêng của cách giải với giá trị Sprague-Grundy này, trong đó giá trị Nim của trò chơi Nim chỉ có một đống $n$ viên sỏi tương đương với giá trị Sprague-Grundy $\text{mex}({0,1,\ldots,n-1}) = n$
Ví dụ với trò chơi Nim chỉ có một đống $3$ viên sỏi
và định lý Bouton tương đương định lý 2.
Định lý Sprague-Grundy
Định lý Sprague-Grundy phát biểu rằng: mọi trò chơi tổ hợp cân bằng kết thúc trong hữu hạn bước đều tương đương với trò chơi Nim một cột, trong đó trạng thái $x$ của trò chơi hiện tại tương ứng với trạng thái trò chơi Nim một cột có $g(x)$ viên sỏi, trong đó $g(x)$ là giá trị Sprague-Grundy của $x$.
Sở dĩ có nhận xét này là vì ở trạng thái $x$ có giá trị Sprague-Grundy $g(x)$, hàm mex cho chúng ta một "lời hứa", lời hứa đó là: từ $x$ với giá trị Sprague-Grundy $g(x)$, ta có thể đi đến tất cả các trạng thái $y$ có giá trị Sprague-Grundy từ $0$ đến $g(x)-1$. Điều này có sự tương đồng với việc trong trò chơi Nim một cột, từ trạng thái $n$ có thể đi đến tất cả trạng thái từ $0$ đến $n-1$.
Tuy nhiên, luật chơi trò chơi Nim một cột này không giống với bình thường, vì trong trò chơi bình thường từ trạng thái $u$ ta chỉ có thể đi tới các trạng thái $v$ có giá trị nhỏ hơn $u$. Tuy nhiên, từ một trạng thái $x$ có giá trị Sprague-Grundy là $g(x)$ ta lại có thể đi đến một trạng thái $y$ có giá trị Sprague-Grundy $g(y) > g(x)$, tương ứng với việc thêm $g(y) - g(x)$ viên sỏi vào trò chơi Nim một cột. Mặc dù vậy, người kia có thể trung hòa thao tác thêm sỏi, làm cho trạng thái của trò chơi quay về trạng thái $g(x)$ bằng cách lấy đi $g(y)-g(x)$ viên sỏi trong lượt tiếp theo. Hơn nữa, vì điều kiện trò chơi sẽ kết thúc trong hữu hạn bước, chắc chắn sẽ có một lúc người chơi không thể thêm sỏi vào nữa và sẽ phải chơi như trò chơi Nim thông thường. Do vậy, ta kết luận trò chơi Nim với phép thêm sỏi không làm kết quả của trò chơi Nim thay đổi so với luật chơi thông thường.
Định lý Sprague-Grundy cho ta sự liên tưởng giữa một trò chơi tổ hợp cân bằng với trò chơi Nim một cột - một trò chơi tổ hợp cân bằng đơn giản, cung cấp cho ta một cách nhìn trực quan hơn về trò chơi tổ hợp cân bằng. Tuy bản thân định lý không có nhiều ứng dụng, nhưng các định lý phụ trợ cho việc chứng minh định lý này lại là nền móng quan trọng cho việc giải các trò chơi tổ hợp cân bằng, chính là các định lý 1 và 2 ở phần trước. Để tránh bài viết quá dài dòng, ở đây sẽ không trình bày lại chứng minh của định lý này, bạn đọc có thể tham khảo thêm về cách chứng minh định lý Sprague-Grundy bằng khái niệm trò chơi tương đương được đề cập đến trong wiki.
Ví dụ
Ta sẽ ví dụ với trò chơi sau
Cho bàn cờ $N \times N$ với $K$ quân mã trên đó. Không giống như quân mã trong cờ vua truyền thống, những quân mã này chỉ có thể di chuyển như thể hiện trong hình bên dưới (vì vậy tọa độ của các con sẽ chỉ bị giảm chứ không tăng, đảm bảo trò chơi kết thúc trong hữu hạn bước). Cùng một lúc có thể có nhiều quân ở cùng một ô của bàn cờ. Hai người chơi thay phiên nhau di chuyển. Khi tới lượt, người chơi chọn một trong các quân mã và di chuyển nó. Người chơi không thể thực hiện nước đi ở lượt của mình là người thua.
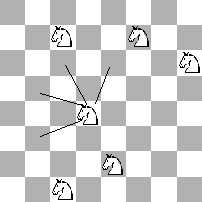
Đầu tiên, vì luật chơi cho phép có nhiều quân mã trên cùng ô nên các quân mã có thể di chuyển độc lập với nhau, như vậy ta có thể coi trò chơi có $K$ quân mã là trò chơi tổng của $K$ trò chơi thành phần, trong đó trò chơi thành phần thứ $i$ chỉ có quân mã thứ $i$ trên bàn cờ.
Ta sẽ giải trò chơi với một quân mã trước. Rõ ràng kết quả của trò chơi khi này chỉ phụ thuộc vào vị trí của quân mã, do đó một trạng thái của trò chơi tương ứng với một cặp số nguyên $(i,j)$ cho biệt vị trí của quân mã. Khi đó ta sẽ tính giá trị Sprague-Grundy của từng vị trí bằng hàm sau
// khai báo các thông tin của trò chơi
const int MAXN = 100;
int N;
int g[MAXN + 1][MAXN + 1];
int di[] = {-2, -2, -1, 1};
int dj[] = {1, -1, -2, -2};
// hàm tính mex của một vector U
int mex(vector<int>& U) {
int res = 0;
sort(U.begin(), U.end());
for (int x: U)
if (res == x)
++res;
return res;
}
int calculateGValue(int i, int j) {
if (g[i][j] != -1)
return g[i][j];
int res = 0;
vector<int> U;
// lấy giá trị SP của các trạng thái mà (i,j) có thể đi tới
for (int k = 0; k < 4; ++k) {
int x = i + di[k];
int y = j + dj[k];
if (1 <= x && x <= N && 1 <= y && y <= N)
U.push_back(calculateGValue(x, y));
}
// tính mex và trả về giá trị
res = mex(U);
g[i][j] = res;
return res;
}Ý tưởng của hàm trên chỉ đơn giản là tại mỗi vị trí $(i,j)$ ta tính mex bằng công thức đệ quy như định nghĩa. Để di chuyển đến các vị trí hợp lệ, ta có hai mảng hằng số di và dj kích thước $4$ tương ứng với bốn bước di chuyển $(i-2,j+1), (i-2,j-1), (i-1,j-2), (i+1,j-2)$ như đề bài miêu tả, với mỗi vị trí ta xét xem vị trí có nằm trên bàn cờ không, nếu có thì mới thêm thêm giá trị Grundy tại vị trí đó vào vector U. Lưu ý là ở đây để tối ưu thời gian chạy thì ta sẽ dùng kỹ thuật đệ quy có nhớ đã trình bày ở phần Trò chơi tổ hợp cân bằng, do đó trước khi gọi tính giá trị Sprague-Grundy của từng ô trong bảng thì phải khởi tạo tất cả giá trị của mảng $g$ bằng $-1$.
Trước tiên, ta định nghĩa cấu trúc dữ liệu để lưu trữ thông tin của một quân mã, đó một struct gồm hai thông tin $row, col$ tương ứng là tọa độ dòng và cột của quân mã.
struct Cell {
int row, col;
};bool isFirstWin(vector<Cell> Q) {
int res = 0;
for (Cell x: Q)
res ^= g[x.row][x.col];
return (res > 0);
}Bài tập luyện tập
Phụ lục
Phần này sẽ chứng minh cơ sở toán học cho hai định lý $1$ và $2$ ở phần Định lý Sprague-Grundy, để hiểu rõ hơn tại sao lại có hai định lý trên, bạn đọc hãy đọc phần này.
Định lý 1: Trong một trò chơi tổ hợp cân bằng, trạng thái $u$ thuộc $P$ khi và chỉ khi giá trị Sprague-Grundy $g(u) = 0$.
Chứng minh:
Tương tự phần trước, ta sẽ gọi $\hat{P}$ là tập các trạng thái có $g(u)=0$ và $\hat{N}$ là tập các trạng thái có $g(u)>0$ và cố gắng chứng minh điều sau: $\hat{P}=P, \: \hat{N}=N$
Thứ nhất, các trạng thái kết thúc $t$ chắc chắn sẽ thuộc $\hat{P}$ do $g(t) = \text{mex}(\varnothing) = 0$.
Thứ hai, với một trạng thái $u$ thuộc $\hat{N}$, khi đó $g(u) > 0$, điều đó có nghĩa là trong các trạng thái $v_1,\ldots,v_k$ đến được từ $u$ luôn tồn tại một trạng thái $v_i$ có $g(v_i) = 0$, tức $v$ thuộc $\hat{P}$. Ta có thể chứng minh dễ dàng bằng phản chứng rằng nếu tất cả các trạng thái $v_1,\ldots,v_k$ đến được từ $u$ có $g(v_i) > 0$ thì rõ ràng phần tử nhỏ nhất không nằm trong tập ${g(v_1),\ldots,g(v_k)}$ là $0$, tức khi đó $g(u) = \text{mex}({g(v_),\ldots,g(v_k)}) = 0$ trái với giả thuyết ban đầu là $g(u) > 0$.
Thứ ba, với mọi trạng thái $u$ thuộc $\hat{P}$ mà $u$ không phải trạng thái kết thúc, khi đó với mọi trạng thái $v_1,\ldots,v_k$ đến được từ $u$ thì $g(v_i) > 0$, tức mọi cách đi từ $u \in \hat{P}$ luôn dẫn đến trạng thái $v \in \hat{N}$. Ta cũng sẽ chứng minh phát biểu này bằng phản chứng, giả sử tồn tại một $v_i$ trong các trạng thái đến được từ $u$ có $g(v_i) = 0$, lúc đó rõ ràng $g(v)=\text{mex}({0,g(v_1),\ldots}) > 0$, trái với giả thuyết ban đầu là $g(u) = 0$.
Từ ba tính chất vừa chứng minh, ta thấy rõ ràng tập $\hat{P}$ và $\hat{N}$ tương đương với tập $P$ và $N$ theo định nghĩa của hai tập này. $\square$
Định lý 2: với trò chơi tổng $G = G_1 + \ldots + G_n$ và $x_1, \ldots, x_n$ lần lượt là các trạng thái của trò chơi thành phần $G_1, \ldots, G_n$, khi đó: $g(x_1, \ldots, x_n) = g_1(x_1) \oplus \ldots \oplus g_n(x_n)$ Với $g, g_1, \ldots, g_n$ lần lượt là hàm Sprague-Grundy của trò chơi $G, G_1, \ldots, G_n$.
Chứng minh:
Do $G$ là một trò chơi tổ hợp cân bằng, do đó theo định lý 1 thì $g(x_1, \ldots, x_n) = mex(\{g(y_1, \ldots, y_n) | (x_1, \ldots, x_n) \rightarrow (y_1, \ldots, y_n) \in Q\})$
Từ đó, nếu gọi $U = {g(y_1, \ldots, y_n) | (x_1, \ldots, x_n) \rightarrow (y_1, \ldots, y_n) \in Q}$, ta thấy nếu muốn chứng minh $g(x_1, \ldots, x_n) = g_1(x_1) \oplus \ldots \oplus g_n(x_n) = s$ thì ta cần chứng minh $\text{mex(U)} = s$
Chi tiết hơn, ta cần chứng minh hai điều sau:
- Với mọi $0 \leq t < s$ thì $t \in U$.
- $s \notin U$
Để chứng minh ý 1, với một $0 \leq t < s$ bất kỳ, ta xét $s \oplus t$, vì $s > 0$ nên biểu diễn nhị phân của $s \oplus t$ luôn tồn tại bit trái nhất bằng $1$ (tạm gọi là $d$).Khi đó, bit thứ $d$ của một trong hai số $s$ và $t$ phải bằng $1$ và bit thứ $d$ của số còn lại bằng bằng $0$. Tuy nhiên, do $s > t$ nên bit thứ $d$ của $s$ bằng $1$ và bit thứ $d$ của $t$ bằng $0$, trường hợp kia không thể xảy ra. Lập luận tiếp rằng $s = g_1(x_1) \oplus \ldots \oplus g_n(x_n)$, tương tự như khi chứng minh định lý Bouton, nếu bit thứ $d$ của $s$ là $1$ thì ta có số lượng $g_i(x_i)$ có giá trị Sprague-Grundy có bit thứ $d$ bằng $1$ phải lẻ (theo tính chất của phép XOR), do đó luôn tồn tại một trò chơi có bit thứ $d$ bằng $1$. Chọn trò chơi mà giá trị Sprague-Grundy có bit thứ $d$ bằng $1$ để thực hiện bốc sỏi, ta thấy $(s \oplus t) \oplus g_i(x_i) < g_i(x_i)$ nên theo định nghĩa hàm Sprague-Grundy chắc chắn tồn tại $x'_i$ có $g_i(x'_i) = (s \oplus t) \oplus g_i(x_i)$ và từ $x_i$ có thể di chuyển đến $x'_i$. Theo định nghĩa trò chơi tổng, khi đó bước di chuyển từ $(x_1,\ldots, x_i, \ldots, x_n)$ tới $(x_1,\ldots, x'_i, \ldots, x_n)$ là hợp lệ và:
Vậy $t \in U$.
Để chứng minh ý 2 ta dùng phản chứng, giả sử trạng thái hiện tại là $(x_1, \ldots, x_n)$, khi đó giả sử tồn tại một trạng thái $(y_1, \ldots, y_n)$ có $g(y_1, \ldots, y_n) = s$. Theo định nghĩa mỗi bước di chuyển trong trò chơi tổng sẽ tương ứng với việc chọn một trò chơi thành phần ra và di chuyển, các trò chơi còn lại giữ nguyên, do đó ta có thể viết $(y_1, \ldots, y_n) = (x_1, \ldots, x'_i, \ldots, x_n)$ với $i$ là trò chơi ta chọn để di chuyển trạng thái. Khi đó
Điều này là mâu thuẫn với giả thuyết ban đầu là ta chọn trò chơi thành phần $i$ để di chuyển trạng thái (khi đó $x'_i \neq x_i$).
Với hai ý được chứng minh này, ta đã chứng minh được định lý 2. $\square$