Đường đi Euler trên cây
Người viết:
- Cao Thanh Hậu - Đại học Khoa học Tự nhiên - ĐHQG-HCM
Reviewer:
- Lê Minh Hoàng - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Trịnh Quang Anh - University of Melbourne
- Nguyễn Anh Bảo - Đại học Bách Khoa Hà Nội
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Hoàng Xuân Nhật - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Ngô Nhật Quang - Trường THPT chuyên Khoa học Tự Nhiên - ĐHQGHN
Giới thiệu
Đường đi Euler trên cây (Euler tour on tree) là một phương pháp hữu dụng được dùng nhiều trong các bài toán trên cây. Đây có thể được hiểu là một cách trải phẳng cây, từ đó các thao tác với cây có thể chuyển về thao tác với dãy một chiều.
Bài toán
Trước khi tìm hiểu sâu hơn về đường đi Euler trên cây, mời bạn đọc xem qua bài toán sau đây.
Truy vấn trên cây
Cho một cây có $n$ đỉnh đánh số từ $1$ đến $n$, đỉnh $1$ là đỉnh gốc của cây. Ban đầu, mỗi đỉnh của cây có giá trị $0$.
Thực hiện các truy vấn thuộc một trong hai loại sau:
- $1$ $u$ $x$: Thay đổi giá trị đỉnh $u$ thành $x$.
- $2$ $u$: Tính tổng giá trị các đỉnh thuộc cây con gốc $u$ (*).
Giới hạn: $n, q \leq 10^5$.
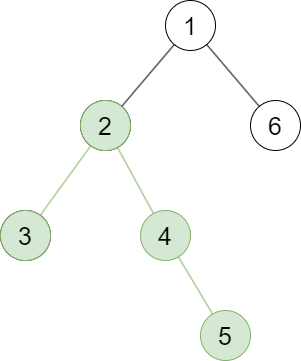
(*): Cây con gốc $u$ là cây tạo bởi tất cả những đỉnh mà đường đi từ đỉnh đó đến đỉnh gốc của cây có chứa $u$, và tất cả những cạnh nối 2 đỉnh mà đường đi từ $2$ đỉnh đó đến đỉnh gốc có chứa đỉnh $u$. Ví dụ, cây trong hình $1$ có gốc cây là đỉnh $1$, với $u = 2$ thì cây con gốc $u$ bao gồm các phần màu xanh lá (cả cạnh và đỉnh).
Thuật toán ngây thơ
Ý tưởng khá đơn giản: duyệt qua tất cả các đỉnh con để tìm đáp án cho truy vấn loại $2$.
const int N = 100000 + 5;
int val[N]; // val[u] là giá trị đỉnh u
int parent[N]; // parent[u] là đỉnh cha của đỉnh u
vector<int> adj[N]; // adj[u] là danh sách các đỉnh kề với đỉnh u
void change(int u, int x) { // thay đổi giá trị đỉnh u
val[u] = x;
}
long long sum(int u) { // tổng các giá trị của cây con gốc u
long long s = val[u];
for (int v : adj[u]) {
if (v != parent[u]) {
s += sum(v);
}
}
return s;
}Độ phức tạp của thuật toán:
- Với các truy vấn loại $1$, ta chỉ thay đổi giá trị của đỉnh nên độ phức tạp cho truy vấn này là $O(1)$.
- Với các truy vấn loại $2$, ta cần duyệt qua tất cả các đỉnh thuộc cây con gốc $u$, trong trường hợp tệ nhất, độ phức tạp cho mỗi truy vấn như thế lên đến $O(n)$.
Vậy thuật toán có độ phức tạp $O(n \times q)$, quá lớn để giải được bài toán này.
Phần sau đây sẽ giới thiệu về một phương pháp rất đặc biệt, có thể được dùng để giải quyết bài toán "hóc búa" trên.
Đường đi Euler trên cây
Định nghĩa
Từ đồ thị cây $T(V, E)$ tạo đồ thị có hướng $T'(V, E')$ theo cách sau: với mỗi cạnh $(u, v) \in E$, thêm vào $E'$ hai cạnh có hướng $(u, v)$ và $(v, u)$.
Thể hiện chu trình Euler (**) trên đồ thị $T'$ bằng một dãy các đỉnh, dãy đỉnh này cũng biểu diễn đường đi Euler trên cây $T$.
(**): Chu trình Euler của một đồ thị là một đường đi trên đồ thị đó, trong đó đỉnh bắt đầu trùng với đỉnh kết thúc của đường đi, và mỗi cạnh của đồ thị được đường đi thăm qua đúng một lần.
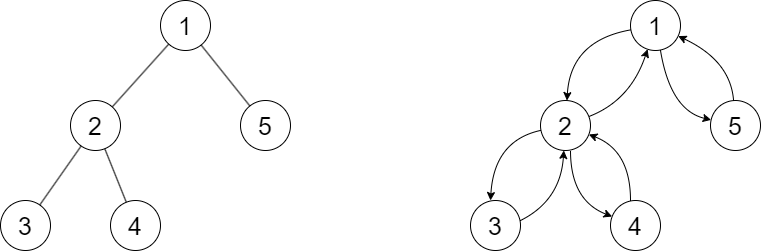
Với đồ thị cây hình $2a$, đường đi Euler biểu diễn bằng dãy các đỉnh: 1 2 3 2 4 2 1 5 1, cũng là dãy các đỉnh biểu diễn chu trình Euler trên đồ thị hình $2b$.

Sự tồn tại của đường đi Euler
Có thể chứng minh rằng, chu trình Euler luôn tồn tại trong đồ thị $T'$, hay $T'$ là đồ thị Euler.
Định lý
Một đồ thị có hướng là đồ thị Euler nếu và chỉ nếu:
- Với mọi đỉnh $u$ thuộc đồ thị, bậc vào của $u$ bằng bậc ra của $u$.
- Mọi đỉnh có bậc khác $0$ thuộc cùng thành phần liên thông.
Chứng minh
Dễ thấy, $T'$ là đồ thị liên thông $(1)$ vì được xây dựng từ một cây.
Mỗi khi xây dựng $2$ cạnh có hướng $(u, v)$ và $(v, u)$ trong $T'$, bậc vào của đỉnh $u$ và $v$ tăng lên $1$, bậc ra của $u$ và $v$ cũng tăng $1$. Vì vậy với mọi đỉnh $p$ trong đồ thị $T'$, bậc vào của $p$ luôn bằng bậc ra của $p$ $(2)$.
Từ $(1)$ và $(2)$ có thể khẳng định, $T'$ là đồ thị Euler.
Cài đặt
Tham khảo đoạn code c++ dưới đây:
#include<bits/stdc++.h>
using namespace std;
const int N = 100000 + 5;
int n, m = 0, root = 1;
int h[N], st[N], en[N], tour[N];
vector<int> adj[N];
// Trong các giá trị bên trên:
// h[u] là khoảng cách từ đỉnh gốc đến đỉnh u.
// st[u] là vị trí đầu tiên của đỉnh u trong mảng tour.
// en[u] là vị trí cuối cùng của đỉnh u trong mảng tour.
void input() {
cin >> n;
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
}
void add(int u) {
tour[++m] = u;
en[u] = m;
}
void dfs(int u, int parent_of_u) {
h[u] = h[parent_of_u] + 1;
add(u);
st[u] = m;
for (int v : adj[u]) {
if (v != parent_of_u) {
dfs(v, u);
}
}
if (u != root) add(parent_of_u);
}
int main() {
input();
dfs(root, 0);
return 0;
}Mỗi khi truy cập một đỉnh bất kỳ, ta thêm đỉnh đó vào đường đi. Trước khi rời khỏi một đỉnh (trở về cha), nếu đỉnh đó khác gốc của cây, ta thêm cha của đỉnh vào đường đi.
Áp dụng code trên vào đồ thị hình $2a$, mảng $tour$ cuối cùng chứa các giá trị: 1 2 3 2 4 2 1 5 1, đây chính là đường đi Euler theo định nghĩa ban đầu.
Tính chất
Như đã giới thiệu, ứng dụng chính của Euler tour là trải phẳng cây, từ đó bài toán trên cây chuyển về bài toán với dãy số. Vậy cụ thể mối liên hệ giữa cây với dãy số là như thế nào, mời bạn đọc cùng tìm hiểu.
Các mối quan hệ về vị trí
Cơ sở
Sau đây là một số tính chất cơ bản nhất của đường đi Euler.
Đỉnh $v$ thuộc cây con gốc $u$ nếu và chỉ nếu $st[u] \leq st[v] \leq en[v] \leq en[u]$.
Đỉnh $v$ không thuộc cây con gốc $u$ và $u$ không thuộc cây con gốc $v$, hay $u$ và $v$ không có quan hệ tổ tiên nếu và chỉ nếu hai đoạn $st[u]..en[u]$ và $st[v]..en[v]$ không giao nhau, nghĩa là $en[u] < st[v]$ hoặc $en[v] < st[u]$.
Từ hai tính chất trên ta nhận xét được rằng, với hai đỉnh $u$, $v$ bất kì, hai đoạn $st[u]..en[u]$ và $st[v]..en[v]$ hoặc là không giao nhau, hoặc một đoạn hoàn toàn bao đoạn còn lại.
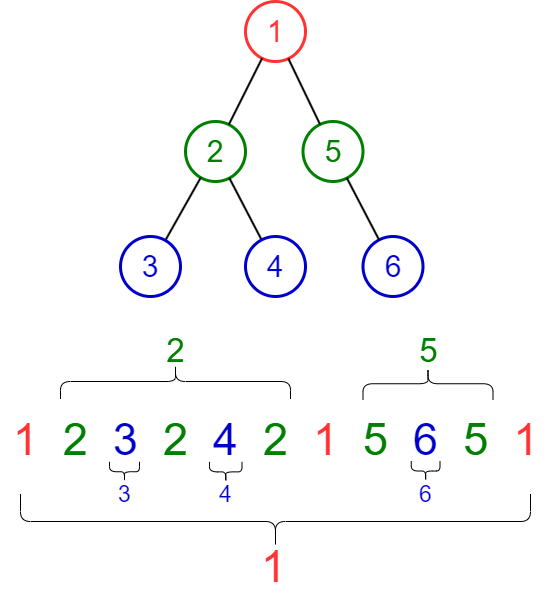
Giải thích
Từ khi thăm đỉnh $u$ lần đầu tiên đến khi thăm đỉnh $u$ lần cuối cùng, đường đi Euler đi qua và chỉ đi qua các đỉnh thuộc cây con gốc $u$. Vậy với mọi đỉnh $v$ thuộc cây con gốc $u$, mọi vị trí của $v$ đều thuộc đoạn $st[u]..en[u]$ (tính chất thứ nhất).
Với hai đỉnh $u$ và $v$ không có quan hệ tổ tiên thì đỉnh $u$ được thăm lần cuối cùng trước khi đỉnh $v$ được thăm lần đầu tiên (hoặc ngược lại, đỉnh $v$ được thăm lần cuối cùng trước khi đỉnh $u$ được thăm lần đầu tiên). Vậy trong trường hợp này $en[u] < st[v]$ hoặc $en[v] < st[u]$ (tính chất thứ hai).
Ứng dụng
Cập nhật, truy vấn đối với đỉnh và cây con
Đây là ứng dụng phổ biến nhất của đường đi Euler trên cây.
Ở ứng dụng này, ta cần thay đổi đường đi Euler một chút.
Gọi $tour$ là dãy biểu diễn đường đi Euler. Với mỗi đỉnh $u$, xóa tất cả các giá trị $u$ xuất hiện trong $tour$ ngoại trừ giá trị $u$ đầu tiên.
Ví dụ, có dãy $tour$ ban đầu gồm các giá trị:
1 2 3 2 4 2 1 5 1
=> 1 2 3 (2) 4 (2) (1) 5 (1)1 2 3 4 5Ta cũng có thể tìm trực tiếp dãy $tour$ (thay vì thay đổi từ dãy đường đi Euler ban đầu) như sau:
void dfs(int u, int parent_of_u) {
tour[++m] = u;
st[u] = m;
for (int v : adj[u]) {
if (v != parent_of_u) {
dfs(v, u);
}
}
en[u] = m;
}Cơ sở
Trong dãy $tour$, tất cả các đỉnh thuộc cây con gốc $u$ nằm liên tiếp từ vị trí $st[u]$ đến vị trí $en[u]$. Tất cả các đỉnh có vị trí thuộc đoạn $st[u]..en[u]$ đều thuộc cây con gốc $u$.
Lưu ý rằng sau khi thay đổi như trên, mỗi đỉnh chỉ xuất hiện trong $tour$ đúng $1$ lần, và ý nghĩa mảng $en$ cũng đã được thay đổi.
Giải thích
Đây thực chất là một cách phát biểu khác của tính chất đầu tiên được nêu ở phần trước: Đỉnh $v$ thuộc cây con gốc $u$ nếu và chỉ nếu $st[u] \leq st[v] \leq en[v] \leq en[u]$.
Và nhận xét rằng tính chất này giữ nguyên tính đúng đắn với dãy $tour$ đã thay đổi.
Vậy về cơ bản, mục đích của việc biến đổi dãy $tour$ nêu trên là để mỗi đỉnh chỉ xuất hiện đúng $1$ lần, sẽ tiện hơn trong xử lý.
Thuật toán
Từ tính chất đó, dễ thấy rằng các thao tác với cây con có thể chuyển thành thao tác với đoạn.
Cụ thể, thao tác cập nhật hoặc truy vấn đối với cây con gốc $u$ có thể chuyển thành thao tác tương ứng đối với đoạn $st[u]..en[u]$.
Ví dụ: Trong đoạn code dưới đây, hàm $change(u, x)$ cho phép tăng giá trị của đỉnh $u$ thêm $x$ đơn vị. Hàm $sum(u)$ cho phép tính tổng giá trị các đỉnh thuộc cây con gốc $u$ (sử dụng kiểu dữ liệu Fenwick Tree - cây BIT).
const int N = 100000 + 5;
int bit[N]; // cây BIT
int st[N], en[N]; // các mảng lưu vị trí đầu tiên / sau cùng của đỉnh, lưu ý rằng mảng en đã có sự thay đổi ý nghĩa
// BIT
void add(int i, int x) {
for (; i <= n; i += i & (-i)) bit[i] += x;
}
long long sumPrefix(int i) {
long long ans = 0;
for (; i > 0; i &= (i - 1)) ans += bit[i];
return ans;
}
// Truy vấn
void change(int u, int v) {
// thay đổi giá trị đỉnh u
add(st[u], x);
}
long long sumSubtree(int u) {
// tính tống đoạn st[u]..en[u]
return sumPrefix(en[u]) - sumPrefix(st[u] - 1);
}Cập nhật đường đi - truy vấn đỉnh
Trong một bài toán cần các thao tác thay đổi giá trị các đỉnh trên đường đi và tính giá trị của đỉnh, ta cũng có thể áp dụng ứng dụng trên để giải quyết.
Gọi:
- $par[u]$ là cha trực tiếp của đỉnh $u$.
- $LCA(u, v)$ là tổ tiên chung gần nhất của $u$ và $v$.
- $b[u]$ là một giá trị khác của đỉnh $u$. Ban đầu, $b[u] = 0$ với mọi $u$.
Giả sử cần tăng giá trị mỗi đỉnh thuộc đường đi từ $u$ đến $v$ thêm $x$ đơn vị, thực hiện các bước như sau:
- Tăng $b[u]$ thêm $x$ đơn vị.
- Tăng $b[v]$ thêm $x$ đơn vị
- Giảm $b[LCA(u, v)]$ đi $x$ đơn vị.
- Giảm $b[par[LCA(u, v)]]$ đi $x$ đơn vị
Để tính giá trị của đỉnh $u$, ta tính tổng các giá trị $b[v]$ mà $v$ thuộc cây con gốc $u$.
Với cách tính như vậy, thì việc cập nhật bên trên sẽ tăng giá trị của những đỉnh thuộc đường đi từ $u$ đến $v$ thêm đúng $x$ đơn vị, giá trị các đỉnh còn lại không thay đổi.
Thật vậy, sau mỗi lần tăng đường đi từ $u$ đến $v$, xét đỉnh $p$:
- Nếu $p$ = $LCA(u, v)$, giá trị đỉnh $p$ tăng thêm $x$ đơn vị do ảnh hưởng của các bước $1, 2, 3$.
- Nếu $p$ thuộc đường đi từ $u$ đến $v$ nhưng không phải $LCA(u, v)$, giá trị đỉnh $p$ tăng thêm $x$ đơn vị do ảnh hưởng của một trong hai bước $1, 2$.
- Nếu $p$ là tổ tiên của $LCA(u, v)$ ($p \ne LCA(u, v)$), giá trị của đỉnh $p$ không thay đổi do chịu ảnh hưởng của cả bốn bước $1, 2, 3, 4$.
- Các trường hợp còn lại, giá trị đỉnh $p$ không thay đổi vì không bị ảnh hưởng bởi bất kì bước nào.
Lưu ý rằng, giá trị đỉnh $u$ bị thay đổi khi một giá trị $b[v]$ mà $v$ thuộc cây con gốc $u$ bị thay đổi.
Các thao tác đối với $b$ là các thao tác dạng "cập nhật đỉnh, truy vấn cây con", vì vậy có thể dễ dàng giải quyết bằng thuật toán đã nêu trước đó.
Cập nhật đỉnh - truy vấn đường đi
Ứng dụng cho phép thay đổi giá trị đỉnh và tính tổng giá trị các đỉnh thuộc đường đi (ngắn nhất) giữa hai đỉnh bất kì trên cây.
Bài toán này có một cách giải khá phổ biến như sau: tạo mảng $f$, trong đó $f[u]$ là tổng giá trị các đỉnh trên đường đi từ đỉnh gốc đến đỉnh $u$. Vậy khi tăng giá trị đỉnh $u$, ta cần tăng các giá trị $f[v]$ mà $v$ thuộc cây con gốc $u$. Và tổng giá trị các đỉnh thuộc đường đi giữa hai đỉnh $u$, $v$ bất kì là $f[u] + f[v] - f[par[LCA(u, v)]$, trong đó $par[LCA(u, v)]$ là cha của tổ tiên chung gần nhất của $u$ và $v$.
Tuy nhiên ứng dụng này muốn đề cập đến một phương pháp khác khá thú vị, mời bạn đọc cùng tìm hiểu.
Trước hết, ta cũng cần thay đổi đường đi Euler như ứng dụng trước, cụ thể:
Theo đường đi Euler, ta thêm đỉnh $u$ vào dãy $tour$ khi thăm đỉnh $u$ lần đầu tiên và khi thăm đỉnh $u$ lần cuối cùng.
(Nếu đỉnh $u$ là lá, ta thêm đỉnh $u$ hai lần liên tiếp vì lần thăm đầu tiên cũng là lần thăm cuối cùng).
Ví dụ
1 2 3 2 4 2 1 5 1
=> 1 2 3 3 4 4 2 5 5 1void dfs(int u, int parent_of_u) {
tour[++m] = u;
st[u] = m;
for (int v : adj[u]) {
if (v != parent_of_u) {
dfs(v, u);
}
}
tour[++m] = u;
en[u] = m;
}$st[u]$ là vị trí đầu tiên của đỉnh $u$, $en[u]$ là vị trí thứ hai của đỉnh $u$. Mỗi đỉnh xuất hiện đúng $2$ lần.
Cơ sở
Với hai đỉnh $u$, $v$ bất kì mà $u$ là tổ tiên của $v$, xét đoạn các giá trị từ vị trí $st[u]$ đến vị trí $st[v]$ của dãy $tour$, ta có:
- Các đỉnh thuộc đường đi từ $u$ đến $v$ xuất hiện đúng $1$ lần trong đoạn, cũng chính là lần đầu tiên đỉnh đó xuất hiện trong dãy $d$.
- Các đỉnh không thuộc đường đi từ $u$ đến $v$ sẽ không xuất hiện lần nào, hoặc xuất hiện đúng hai lần trong đoạn.
Ví dụ:
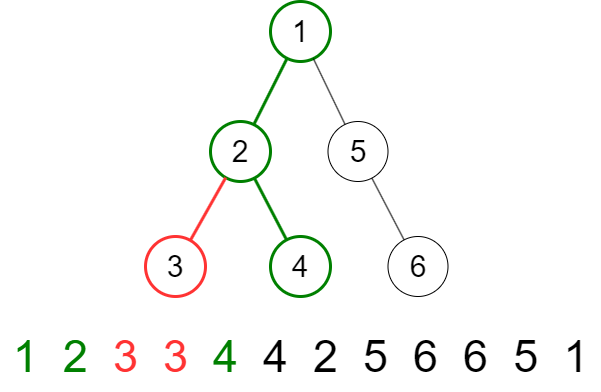
Các đỉnh được tô màu khác màu đen là các đỉnh xuất hiện trong đoạn $st[1]..st[4]$ của dãy.
Giải thích
Do $u$ là tổ tiên của $v$ ta có $st[u] \leq st[v] \leq en[v] \leq en[u]$.
Trước tiên, ta không cần quan tâm đến những đỉnh không xuất hiện trong đoạn $st[u]..st[v]$ của dãy $d$, vì những đoạn thuộc đường đi từ $u$ đến $v$ trên cây thì chắc chắn xuất hiện trong đoạn này.
Xét đỉnh $p$ xuất hiện trong đoạn $st[u]..st[v]$ của dãy $d$:
- Nếu $p$ thuộc đường đi từ $u$ đến $v$ trên cây, nghĩa là $v$ thuộc cây con gốc $p$ và $p$ thuộc cây con gốc $u$, vậy $st[u] \leq st[p] \leq st[v] < en[p]$, $p$ xuất hiện đúng $1$ lần trên đoạn $st[u]..st[v]$, cũng là lần thứ nhất đỉnh $p$ xuất hiện trong dãy $d$.
- Nếu $p$ không thuộc đường đi từ $u$ đến $v$ trên cây, nghĩa là $p$ không có quan hệ tổ tiên với $v$, ta có $st[u] < st[p] < en[p] < st[v]$, vậy $p$ xuất hiện đủ $2$ lần trên đoạn.
Thuật toán
Ý tưởng của thuật toán này là tạo mảng $f$ với $f[st[u]]$ là giá trị của đỉnh $u$, và $f[en[u]] = -f[st[u]]$. Vì vậy khi tính tổng giá trị đoạn $st[u]..st[v]$ của mảng $f$, các đỉnh $p$ xuất hiện $2$ lần sẽ tự "triệt tiêu" do $f[st[p]] + f[en[p]] = 0$, chỉ còn lại tổng các đỉnh xuất hiện một lần - các đỉnh thuộc đường đi từ $u$ đến $v$.
Ta có thuật toán như sau:
- Khi tăng giá trị đỉnh $u$ thêm $x$ đơn vị, ta tăng giá trị tại vị trí $st[u]$ thêm $x$ đơn vị, giảm giá trị tại vị trí $en[u]$ đi $x$ đơn vị.
- Để tính tổng giá trị các đỉnh trên đường đi từ $u$ đến $v$, ta tính tổng các giá trị thuộc đoạn $st[u]..st[v]$ (giả sử $u$ là tổ tiên của $v$).
Thuật toán chỉ áp dụng đối với đường đi từ một tổ tiên của một đỉnh về đỉnh đó. Đối với trường hợp tổng quát của $u$ và $v$, cần chia đường đi thành 2 phần là $[LCA(u, v)..u]$ và $[LCA(u, v)..v]$, hai đường đi này thỏa điều kiện trên.
Tổ tiên chung gần nhất - Lowest Common Ancestor
Đường đi Euler trên cây cũng có thể được dùng để tìm tổ tiên chung gần nhất, kết hợp với cấu trúc dữ liệu RMQ.
Ứng dụng này không cần biến đổi đường đi Euler.

Cơ sở
Gọi:
- $tour$ là dãy đỉnh biểu diễn đường đi Euler.
- $st[u]$ là vị trí đầu tiên của đỉnh $u$ trong dãy $tour$.
Ta có tính chất sau:
Đối với hai đỉnh $u$, $v$ phân biệt mà $st[u] \leq st[v]$, tổ tiên chung gần nhất của hai đỉnh này là giá trị $p$ thuộc đoạn $st[u]..st[v]$ của dãy $tour$ sao cho khoảng cách từ $p$ đến gốc là nhỏ nhất có thể.
Giải thích
Gọi $p$ là cha chung gần nhất của $u$ và $v$.
Xét các đỉnh xuất hiện trên đoạn $st[u]..st[v]$ của dãy $tour$:
- Theo định nghĩa, đoạn này thể hiện một đoạn của đường đi Euler, bắt đầu từ đỉnh $u$ và đi đến đỉnh $v$, vì vậy chắc chắn có chứa đỉnh $p$.
- Vì $v$ là con của $p$ nên đoạn này không thể chứa bất cứ đỉnh nào là tổ tiên của $p$.
Vậy đỉnh gần gốc nhất trên đoạn $st[u]..st[v]$ chính là đỉnh $p$ - tổ tiên chung gần nhất của $u$ và $v$.
Thuật toán
Gọi $h[u]$ là khoảng cách của đỉnh $u$ đến gốc của cây. Khi tìm $LCA(u, v)$, ta cần tìm đỉnh $p$ thuộc đoạn $st[u]..st[v]$ mà $h[p]$ là nhỏ nhất.
Có thể áp dụng cấu trúc dữ liệu RMQ để tìm đỉnh $p$, độ phức tạp cho việc chuẩn bị là $O(M * log(M))$, độ phức tạp cho mỗi thao tác tìm $LCA$ là $O(1)$, trong đó, $M$ là độ dài của mảng lưu đường đi Euler.
Lưu ý rằng, độ dài của mảng lưu đường đi Euler có thể lớn hơn $n$, cụ thể $M = 2 * (n - 1) + 1$, vì mỗi cạnh được đi qua $2$ lần, mỗi lần qua một cạnh thì thêm một đỉnh vào đường đi, ngoại trừ cạnh đầu tiên thêm hai đỉnh vào đường đi.
Bài tập ví dụ: Company Queries II
Một công ty nọ có $n$ thành viên. Ngoại trừ tổng giám đốc, mỗi thành viên sẽ có một người sếp.
Cho thông tin về số thành viên và sếp của mỗi người, hãy trả lời $q$ truy vấn dạng $a$ $b$ với câu hỏi: ai là sếp chung thấp nhất của $a$ và $b$.
Giới hạn: $n, q \leq 2 \times 10^5$
Dưới đây là đoạn code mẫu cho bài tập trên:
#include <bits/stdc++.h>
using namespace std;
const int N = 200000 + 5;
const int K = 20;
int n, q, m = 0, h[N], st[N];
int R[2 * N][K];
//R[i][j] là giá trị u có st[u] thuộc đoạn i..i+(2^j)-1 sao cho h[u] là nhỏ nhất
vector<int> g[N];
void dfs(int u, int p) {
h[u] = h[p] + 1;
R[++m][0] = u;
st[u] = m;
for (int v : g[u]) {
if (v != p) {
dfs(v, u);
R[++m][0] = u;
}
}
}
void solve() {
cin >> n >> q;
for (int i = 2; i <= n; ++i) {
int p; cin >> p;
g[p].push_back(i);
}
dfs(1, 0);
for (int k = 0; (1 << (k + 1)) <= m; ++k) {
for (int i = 1; i + (1 << (k + 1)) - 1 <= m; ++i) {
R[i][k + 1] = (h[R[i][k]] < h[R[i + (1 << k)][k]] ? R[i][k] : R[i + (1 << k)][k]);
}
}
while (q--) {
int u, v;
cin >> u >> v;
int l = st[u], r = st[v];
if (l > r) swap(l, r);
int k = log2(r - l + 1);
cout << (h[R[l][k]] < h[R[r - (1 << k) + 1][k]] ? R[l][k] : R[r - (1 << k) + 1][k]) << "\n";
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
solve();
return 0;
}