Quy hoạch động cơ bản (Phần 2)
Bài viết được sưu tầm và bổ sung từ bài viết "Một số bài toán quy hoạch động kinh điển" của thầy Nguyễn Thanh Tùng, Tạp chí Tin học và Nhà trường số $1$, năm $2005$.
Người viết: Nguyễn Anh Bảo - Đại học Bách Khoa Hà Nội
Reviewer:
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên, ĐHQG-HCM
- Ngô Nhật Quang - Trường THPT chuyên Khoa học Tự Nhiên, ĐHQGHN
Giới thiệu
Ở phần trước, chúng ta đã được làm quen với khái niệm Quy hoạch động đồng thời xem xét một số bài toán điển hình. Bài viết này nhằm giới thiệu thêm một số bài toán quy hoạch động thường gặp khác.
1. Biến đổi xâu
Để thuận tiện cho việc trình bày và tính toán, trong mục $(1)$ ta sẽ quy ước các xâu đều bắt đầu từ chỉ số $1$.
1.1. Mô hình
Cho hai xâu $A$, $B$ có độ dài lần lượt là $m$ và $n$, bắt đầu từ chỉ số $1$. Ta muốn biến đổi xâu $A$ về xâu $B$ qua một số phép biến đổi thuộc các loại sau:
- Chèn kí tự $C$ vào sau kí tự thứ $i$:
I i C,icó thể bằng $0$- Thay thế kí tự ở vị trí thứ $i$ bằng kí tự $C$:
R i C- Xoá kí tự ở vị trí thứ $i$:
D iHãy tìm số ít nhất các phép biến đổi để biến xâu $A$ thành xâu $B$. Điều kiện: $1\le n \times m \le 10^6$.
Ví dụ 1: ILoveVNOI$\to$ILoveVNOIMore
| Lượt biến đổi | Phép biến đổi | A |
|---|---|---|
| $1$ | I 9 e |
ILoveVNOIe |
| $2$ | I 9 r |
ILoveVNOIre |
| $3$ | I 9 o |
ILoveVNOIore |
| $4$ | I 9 M |
ILoveVNOIMore |
Ví dụ 2: asrefghuar$\to$regular
| Lượt biến đổi | Phép biến đổi | A |
|---|---|---|
| $1$ | R 8 l |
asrefghlar |
| $2$ | R 7 u |
asrefgular |
| $3$ | D 5 |
asregular |
| $4$ | D 1 |
sregular |
| $5$ | D 1 |
regular |
Ví dụ 3: D9M12Y2022$\to$D1M1Y2023
| Lượt biến đổi | Phép biến đổi | A |
|---|---|---|
| $1$ | R 2 1 |
D1M12Y2022 |
| $2$ | R 10 3 |
D1M12Y2023 |
| $3$ | D 5 |
D1M1Y2023 |
1.2. Lời giải
Chú ý: Chỉ số bắt đầu của $A$ và $B$ là $1$, không phải $0$.
Đặt $A_i$ là xâu gồm $i$ kí tự đầu tiên của $A$, $B_j$ là xâu gồm $j$ kí tự đầu của $B$. Quy ước $A_0$ và $B_0$ là 2 xâu rỗng (có $0$ kí tự).
Ý tưởng bài toán này là quy hoạch động mảng $L[i][j]$ - số phép biến đổi ít nhất để biến xâu $A_i$ thành xâu $B_j$.
Dễ thấy $L[0][j]=j$ và $L[i][0]=i$.
Ta đi tìm công thức truy hồi:
Có 2 trường hợp xảy ra:
- Nếu $A[i] = B[j] = C$: Cần biến xâu $A_{i-1}C$ thành xâu $B_{j-1}C$. Để biến đổi tối ưu, cần biến đổi xâu $A_{i-1}$ thành xâu $B_{j-1}$ sau ít phép biến đổi nhất, giữ nguyên kí tự $C$. Số phép biến đổi cần thiết là $L[i - 1][ j - 1]$.
- Nếu $A[i] = C \ne B[j] = D$: Để biến đổi $A_{i-1}C$ thành $B_{j-1}D$, ta có thể dùng một trong các cách sau:
- Xoá kí tự $C$: Sau khi xóa, cần biến $A_{i-1}$ thành $B_{j}$. Số phép biến đổi ít nhất là $L[i-1][j]$. Do đó số phép biến đổi phải dùng là $L[i-1][j]+1$.
- Thay thế $C$ bởi $D$: Sau đó, cần biến $A_{i-1}D$ thành $B_{j-1}D$. Số phép biến đổi ít nhất là $L[i-1][j-1]+1$.
- Chèn $D$ vào sau $C$: Sau đó, cần biến đổi $A_{i}D$ thành $B_{j-1}D$. Số phép biến đổi ít nhất là $L[i][j -1] + 1$.
- Các cách biến đổi khác đều phải chứa phép biến đổi $1,2$ hoặc $3$. Do đó, ta có thể đảo thứ tự các phép biến đổi để đưa về lần biến đổi đầu tiên là $1,2$ hoặc $3$.
Tổng kết lại, ta có công thức QHĐ sau:
- $L[0][j]=j$, với mọi $j=0,1,\ldots,n$.
- $L[i][0]=i$, với mọi $i=0,1,\ldots,m$.
- $L[i][j] =L[i−1][j−1]$ nếu $A[i] = B[j]$.
- $L[i][j] = \min(L[i−1][j], L[i][j−1], L[i−1][j−1]) + 1$ nếu $A[i] \ne B[j]$.
Bài này ta có thể tiết kiệm biến hơn bằng cách dùng 2 mảng 1 chiều tính lẫn nhau và một mảng đánh dấu 2 chiều để truy vết.
1.3. Code tham khảo
Cần lưu ý thứ tự tính. Để tính $L[i][j]$ cần biết $L[i - 1][j -1],L[i-1][j]$ và $L[i][j-1]$. Hơn nữa, $L[i][0]$ và $L[0][j]$ có thể tính trực tiếp nên ta có thể tính theo trình tự sau:
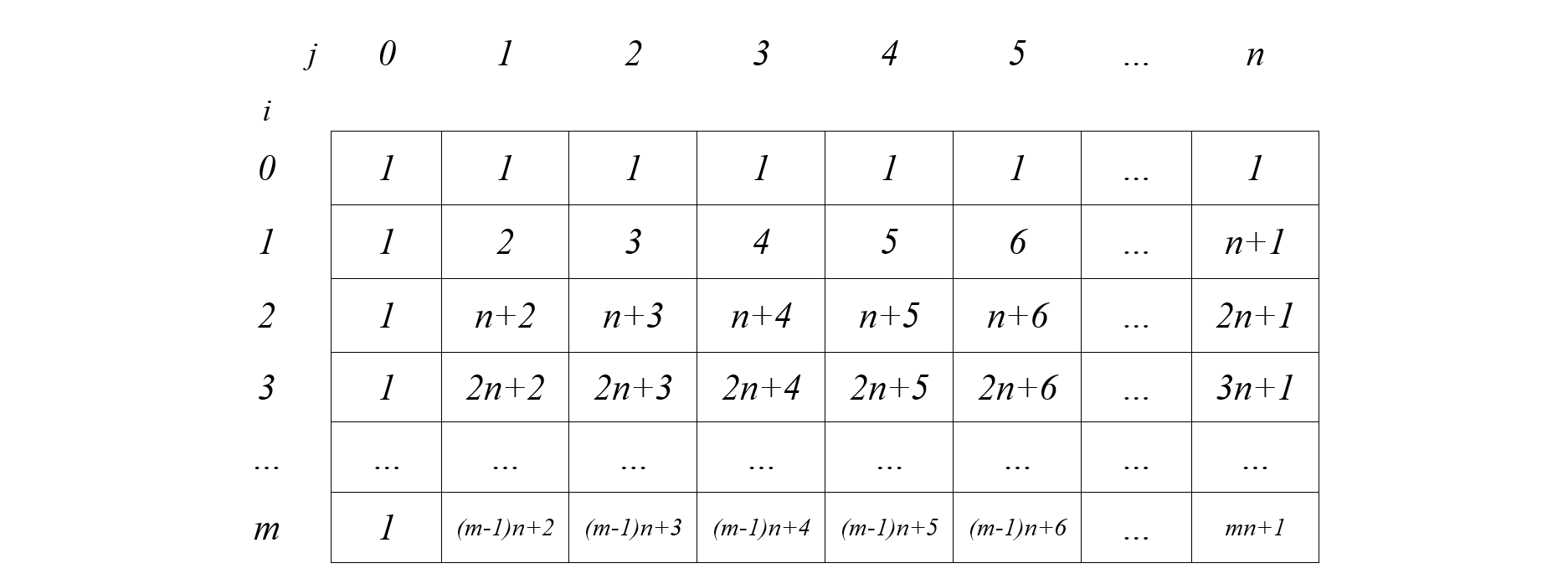
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int m, n;
string a, b;
vector<vector<int>> L;
int main()
{
cin >> a >> b;
m = a.length();
n = b.length();
L.resize(m + 1);
for (auto& i : L)
i.resize(n + 1);
/* Vì a và b bắt đầu từ chỉ số 1 nên
* chèn thêm 1 kí tự vào đầu 2 xâu */
a = "_" + a;
b = "_" + b;
for (int i = 0; i <= m; i++)
L[i][0] = i;
for (int j = 0; j <= n; j++)
L[0][j] = j;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
{
if (a[i] == b[j])
L[i][j] = L[i - 1][j - 1];
else
L[i][j] = 1 + min(L[i - 1][j - 1],
min(L[i - 1][j], L[i][j - 1]));
}
cout << L[m][n];
}1.4. Một số bài toán khác
1.4.1. Xâu con chung dài nhất
Link nộp bài: VNOJ-LCS
Cho $2$ xâu A và B. Tìm xâu con chung dài nhất của $A$ và $B$. Xâu $X$ là xâu con của xâu $Y$ khi và chỉ khi có thể thu được $X$ bằng cách xóa một số kí tự của $Y$ (có thể tất cả hoặc không kí tự nào). Điều kiện: $1\le |A|\times |B| \le 10^6$. Input: $2$ xâu $A$ và $B$. Output: Độ dài xâu con chung dài nhất.
Lời giải:
Gọi $L[i][j]$ là độ dài xâu con chung dài nhất của xâu $A_i$ gồm $i$ kí tự phần đầu của $A$ ($A_i = A[1..i]$) và xâu $B_j$ gồm $j$ kí tự phần đầu của $B$ ($B_j = B[1..j]$).
- Nếu $A[i]=B[j]$ thì ta chỉ cần chọn xâu con dài nhất của $A_{i-1}$ và $B_{j-1}$, do đó độ dài xâu con dài nhất của $A_i$ và $B_j$ là $L[i-1][j-1]+1$.
- Nếu $A[i]\ne B[j]$ thì xâu con chung dài nhất sẽ là xâu con của $A_{i-1}$ và $B_j$ hoặc $A_i$ và $B_{i-1}$.
Từ đó có công thức quy hoạch động như sau:
- $L[0][j] = L[i][0] = 0$
- $L[i][j] = L[i−1][j−1] + 1$ nếu $A[i] = B[j]$
- $L[i][j] = \max(L[i−1][j], L[i][j−1])$ nếu $A[i] \ne B[j]$.
Cài đặt:
Lưu ý do $m$ và $n$ có thể lớn đến $10^6$ nên mảng $L$ phải là mảng động (ví dụ std::vector trong c++).
Nếu đề bài yêu cầu phải in ra xâu con dài nhất thì phải thực hiện truy vết. Dưới đây là một cách cài đặt tham khảo:
#include <iostream>
#include <string>
#include <vector>
using namespace std;
// Struct dùng để truy vết
struct Trace
{
// Vị trí của kí tự trước đó trong A và B
int i;
int j;
// Kí tự cần thêm vào xâu kết quả
// (có thể là kí tự NULL)
char c;
Trace(int ii = 0, int jj = 0, char cc = '\0')
: i(ii), j(jj), c(cc)
{ };
};
int m, n;
string a, b;
vector<vector<int>> L;
vector<vector<Trace>> Tr;
int main()
{
cin >> a >> b;
m = a.length();
n = b.length();
L.resize(m + 1);
Tr.resize(m + 1);
for (auto& i : L)
i.resize(n + 1);
for (auto& i : Tr)
i.resize(n + 1);
// Vì a và b bắt đầu từ chỉ số 1 nên
// chèn thêm 1 kí tự vào đầu 2 xâu
a = "_" + a;
b = "_" + b;
for (int i = 0; i <= m; i++)
L[i][0] = 0;
for (int j = 0; j <= n; j++)
L[0][j] = 0;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
{
if (a[i] == b[j])
{
L[i][j] = L[i - 1][j - 1] + 1;
Tr[i][j] = Trace(i - 1, j - 1, a[i]);
}
else if (L[i - 1][j] > L[i][j - 1])
{
L[i][j] = L[i - 1][j];
Tr[i][j] = Trace(i - 1, j);
}
else
{
L[i][j] = L[i][j - 1];
Tr[i][j] = Trace(i, j - 1);
}
}
// Truy vết xâu con chung dài nhất từ Tr[m][n]
Trace t = Tr[m][n];
string ans = "";
while (true)
{
if (t.c != '\0')
ans = t.c + ans;
if (t.i == 0 && t.j == 0)
break;
else
t = Tr[t.i][t.j];
}
cout << ans;
}Như vậy độ phức tạp bộ nhớ của bài toán là $\mathcal{O}(mn)$, độ phức tạp thời gian là $\mathcal{O}(mn)$.
Có một phương pháp cài đặt tốt hơn, chỉ với độ phức tạp bộ nhớ $\mathcal{O}(\min(m, n))$ dựa trên nhận xét ở ví dụ đầu:
Để tính $L[i][j]$, ta chỉ cần 3 ô $L[i-1][j-1]$, $L[i-1][j]$ và $L[i][j-1]$.
Tức là để tính hàng $L[i]$ thì chỉ cần hàng $L[i-1]$ và $L[i][0] = 0$. Do đó ta chỉ cần 2 mảng 1 chiều để lưu hàng vừa tính $P$ và hàng đang tính $L$. Cách cài đặt mới như sau:
vector<int> P(n + 1), L(n + 1);
for (int i = 1; i <= m; i++)
{
L[0] = 0;
for (int j = 1; j <= n; j++)
if (a[i] == b[j])
L[j] = P[j - 1] + 1;
else
L[j] = max(L[j - 1], P[j]);
P = L;
}1.4.2. Bắc cầu
Hai nước Alpha và Beta nằm ở hai bên bờ sông Omega, Alpha nằm ở bờ bắc và có $m$ thành phố được đánh số từ $1$ đến $m$, Beta nằm ở bờ nam và có $n$ thành phố được đánh số từ $1$ đến $n$ (theo vị trí từ tây sang đông). Mỗi thành phố của nước này thường có quan hệ kết nghĩa với một số thành phố của nước kia. Để tăng cường tình hữu nghị, hai nước muốn xây các cây cầu bắc qua sông, mỗi cây cầu sẽ là nhịp cầu nối 2 thành phố kết nghĩa. Với yêu cầu là các cây cầu không được cắt nhau và mỗi thành phố chỉ là đầu cầu cho nhiều nhất là một cây cầu, hãy đếm số cây cầu nhiều nhất có thể xây dựng. Điều kiện: $1\le n \times m \le 10^6$.
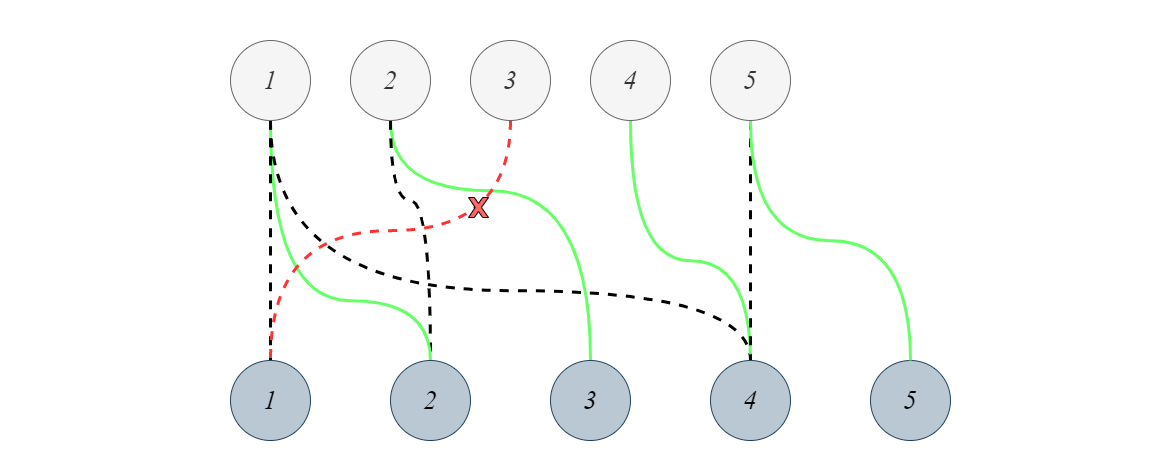
Lời giải:
Bài toán có thể được phát biểu lại như sau: Cho đồ thị hai phía $G(A,B,E)$. Các đỉnh của $A$ là $a_1,a_2,\ldots,a_m$. Tương tự, các đỉnh của $B$ là $b_1,b_2,\ldots,b_n$. Cần tìm $k$ lớn nhất để có hai dãy đỉnh $a'_1 < a'_2 < \ldots < a'_k\in A$ và $b'_1 < b'_2 < \ldots < b'_k\in B$ sao cho: $(a'_i,b'_i)\in E$ với mọi $i=1;2;\ldots;k$.
Ý tưởng tương tự như các bài trên, ta xét mảng $L[i][j]$ là số lượng cầu nhiều nhất có thể bắc từ các thành phố $a_1,a_2,\ldots,a_i$ đến $b_1,b_2,\ldots,b_j$.
Khi đó công thức QHĐ sẽ là:
- $L[i][0] =0,L[0][j] = 0$
- $L[i][j] = 1 + L[i-1][j-1]$ nếu $a_i$ và $b_j$ là hai thành phố kết nghĩa
- $L[i][j] = \max(L[i][j-1], L[i-1][j])$ nếu $a_i$ và $b_j$ không là hai thành phố kết nghĩa
Nhận xét: Không mất tổng quát, giả sử thứ tự xây các cây cầu là tăng dần theo mút ở thành phố $A$. Khi đó, nếu ta đã chọn xây cầu giữa hai thành phố $a_i$ và $b_j$ thì cây cầu tiếp theo, giả sử là cây cầu nối $a_u$ và $b_v$ sẽ phải thỏa mãn $u>i,v>j$. Do đó, bài toán có thể giải như bài toán tìm xâu con dài nhất, với $a_i$ và $b_j$ được xem là "bằng nhau" khi và chỉ khi chúng là hai thành phố kết nghĩa.
1.4.3. Palindrome (IOI 2000)
Link nộp bài: SPOJ - IOIPALIN
Cho một xâu $S$. Ở mỗi bước, bạn An có thể chèn $1$ kí tự tùy ý vào bất kì vị trí nào trong xâu $S$. Hãy tính số bước ít nhất cần thực hiện để biến $S$ thành xâu đối xứng. Xâu $S[1..n]$ được gọi là xâu đối xứng nếu $S[i] = S[n + 1 - i]$, với mọi $i=1;2;\ldots;n$. Điều kiện: $1\le|S|\le5000$.
Lời giải:
Cách 1: Công thức QHĐ của bài này như sau:
Gọi $L[i][j]$ là số kí tự ít nhất cần thêm vào xâu con $S[i..j]$ của $S$ để xâu đó trở thành đối xứng. Nhận xét đầu tiên là xâu thu được sau khi thêm một số kí tự vào $S[i..j]$ phải có kí tự đầu tiên và cuối cùng là $S[i]$ hoặc $S[j]$.
- Nếu $S[i] = S[j]$ thì xâu đối xứng thu được từ $S[i][j]$ cũng có kí tự đầu tiên là $S[i]$ và kí tự cuối cùng là $S[j]$. Do đó, chỉ cần tìm số kí tự ít nhất để thêm vào $S[i+1][j-1]$ để tạo thành xâu đối xứng.
- Nếu $S[i]\ne S[j]$ thì trước tiên ta cần thêm kí tự $S[j]$ vào đầu hoặc $S[i]$ vào cuối xâu $S[i..j]$. Do đó, chỉ cần tìm số kí tự ít nhất cần thêm vào để $S[i][j-1]$ hoặc $S[i+1][j]$ trở thành xâu đối xứng.
Tóm lại, công thức QHĐ là:
- $L[i][j]=0$ nếu $i\ge j$
- $L[i][j]=L[i+1][j-1]$ nếu $i < j$ và $S_i=S_j$
- $L[i][j]=1 + \min(L[i+1][j], L[i][j-1])$ nếu $i < j$ và $S_i \ne S_j$
Đáp số của bài toán sẽ là $L[1][n]$ với $n$ là số kí tự của $S$.
Cài đặt: Ta có thể cài đặt trực tiếp thuật toán trên mà không cần quan tâm đến thứ tự tính như sau:
#include <iostream>
#include <string>
using namespace std;
const int N = 5010;
int n, d[N][N];
string s;
int calc(int i, int j)
{
// Nếu L[i, j] chưa được tính thì lưu giá trị vào d[i][j]
if (d[i][j] == -1)
{
if (i >= j)
d[i][j] = 0;
else
{
if (s[i] == s[j])
d[i][j] = calc(i + 1, j - 1);
else
d[i][j] = 1 + min(calc(i, j - 1), calc(i + 1, j));
}
}
return d[i][j];
}
int main()
{
cin >> s;
n = s.length();
s = "_" + s;
for (int i = 0; i <= n; i++)
for (int j = 0; j <= n; j++)
d[i][j] = -1;
cout << calc(1, n) << '\n';
}Nhận xét: Đây là phương pháp đệ quy có nhớ (memoization). Độ phức tạp bộ nhớ của thuật toán là $\mathcal{O}(n^2)$. Có một phương pháp cài đặt tiết kiệm hơn như sau:
Để ý để tính được mảng $L[1..n][j]$ thì ta chỉ cần mảng $L[1..n][j - 1]$. Do đó ta sẽ dùng hai mảng một chiều $P$ và $L$ để lưu giá trị mảng đã tính và cần tính. Ở mỗi vòng lặp ta có $P=L[1..n][j-1],L=L[1..n][j]$. Đáp án bài toán là $L[1]$.
Cách 2: Từ ý tưởng của bài xâu con chung dài nhất, ta có thuật toán sau:
- Gọi $P$ là xâu đảo của $S$ và $T$ là xâu con chung dài nhất của $S$ và $P$. Khi đó các kí tự của $S$ không thuộc $T$ cũng là các kí tự cần thêm vào để $S$ trở thành đối xứng. Đáp số của bài toán sẽ là $n-k$, với $k$ là độ dài của $T$.
Ví dụ: $S=edbabcd$, xâu đảo của $S$ là $P=dcbabde$. Xâu con chung dài nhất của $S$ và $P$ là $T=dbabd$. Như vậy cần thêm $|S|-|T|=7-5=2$ kí tự vào $S$ để $S$ trở thành xâu đối xứng. Ví dụ, ta có thể thêm kí tự e và c vào $S$ và thu được xâu $S=edcbabcde$.
2. Xếp vali không giới hạn (Unbounded Knapsack)
2.1. Mô hình
Có $n$ đồ vật, vật thứ $i$ có trọng lượng $A_i$ và giá trị $B_i$. Hãy chọn ra một số các đồ vật để xếp vào vali có trọng lượng tối đa $W$ sao cho tổng giá trị của vali là lớn nhất (Chú ý mỗi vật có thể chọn nhiều lần). Điều kiện: $1\le n\times W\le 10^6,1\le A_i,B_i\le 10^9$.

Chú ý: Bài toán này khác với bài toán Xếp Vali ở phần trước ở chỗ mỗi vật không phải là duy nhất và có thể được chọn vào vali nhiều lần.
2.2. Lời giải
Trạng thái của bài toán phụ thuộc vào hai yếu tố: số vật đang được chọn và tổng khối lượng của chúng. Ta có thể gọi $L[i][ j]$ là giá trị lớn nhất có thể có khi ta chọn các vật từ $1$ đến $i$ sao cho khối lượng của chúng không vượt quá $j$. Khi đó, đáp số bài toán sẽ là $L[n][W]$.
Ta đi tìm công thức truy hồi của $L[i][j]$:
- $L[i][ 0] = 0$
- $L[0][ j] = 0$
- $L[i][j] = L[i -1, j]$ nếu $A_i > j$
- $L[i][j] = \max(L[i-1][j],L[i][ j-A_i] + B_i)$ nếu $A_i\le j$
Trong đó, $L[i-1][j]$ là giá trị có được nếu không được đưa vật $i$ vào balô, $L[i][j-A_i] + B_i$ là giá trị có được nếu được phép đưa vật $i$ vào balô.
2.3. Code tham khảo
Tương tự như các ví dụ trước, ta có thể dùng mảng hai chiều $L[i][j]$ để lưu kết quả bài toán. Khi tính, ta có thể tính theo từng hàng hoặc đệ quy có nhớ. Cả hai cách đểu có độ phức tạp thời gian và bộ nhớ $\mathcal{O}(nW)$.
Để giảm độ phức tạp bộ nhớ xuống $\mathcal{O}(n)$, ở mỗi bước ta chỉ cần lưu kết quả của hai hàng vừa tính ($L[i-1]$ và $L[i]$). Ta có thể cài đặt như sau:
#include <iostream>
#include <vector>
using namespace std;
long long n, w;
vector<long long> a, b, L, P;
int main()
{
cin >> n >> w;
a.resize(n + 1);
b.resize(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i] >> b[i];
P = L = vector<long long>(w + 1);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= w; j++)
{
if (a[i] > j)
L[j] = P[j];
else
L[j] = max(P[j], L[j - a[i]] + b[i]);
}
P = L;
}
cout << L[w];
}Lưu ý rằng đoạn chương trình trên mới chỉ cài đặt y nguyên công thức QHĐ chứ chưa tối ưu. Ví dụ với các $j<A_i$, ta gán $L[j]=P[j]$ nhưng sau đó lại gán $P=L$. Bạn đọc có thể rút gọn đoạn code lại để chương trình tối ưu hơn.
2.4. Một số bài toán khác
2.4.1. Đổi tiền
Ở đất nước Omega người ta chỉ tiêu tiền xu. Có $n$ loại tiền xu, loại thứ $i$ có mệnh giá là $A_i$ đồng. Một người khách du lịch đến Omega du lịch với số tiền $m$ đồng. Ông ta muốn đổi số tiền đó ra tiền xu Omega để tiện tiêu dùng. Ông ta cũng muốn số đồng tiền sau khi đổi là ít nhất (cho túi tiền đỡ nặng khi đi đây đi đó). Bạn hãy giúp ông ta tìm cách đổi tiền. Điều kiện: $1\le n \times m\le 10^6,1\le A_i\le 10^9$. Input: Hai số $m,n$ và $A_1,A_2,\ldots,A_n$. Output: Nếu không thể đổi được, in ra $-1$. Ngược lại, in ra hai dòng:
- Dòng đầu tiên in ra số đồng tiền ít nhất có thể.
- Dòng thứ hai in ra $n$ số, số thứ $i$ là số đồng xu của mệnh giá thứ $i$.
Lời giải:
Nếu xem "khối lượng" là mệnh giá và "giá trị" bằng $1$, bài toán này sẽ được phát biểu lại thành: xếp các vật có tổng khối lượng đúng bằng $m$ vào vali sao cho tổng giá trị của chúng là nhỏ nhất. Lưu ý trong mô hình bài toán gốc thì tổng giá trị phải là lớn nhất, và tổng khối lượng có thể bé hơn $m$.
Ta xây dựng mảng $L[i][j]$ là số đồng xu (giá trị) nhỏ nhất có thể khi đổi $j$ đồng (khối lượng) ra tiền xu bằng $i$ loại tiền $A_1,A_2,\ldots,A_i$. Công thức truy hồi của mảng $L$ như sau:
- $L[0][j] = \inf$
- $L[i][0] = 0$
- $L[i][j] = L[i - 1][j]$ nếu $A_i > j$
- $L[i][j] = \min(L[i - 1][j], L[i][j - A_i] + 1)$ nếu $A_i\le j$
Kết quả của bài toán là $L[n][m]$ hoặc $-1$ nếu $L[n][m ]=\inf$. Để truy vết các đồng tiền được đổi, ta có thể dùng mảng $d[i][j]\in {1;2;\ldots;n}$ là chỉ số của đồng tiền được thêm vào khi tính $L[i][j]$.
Cài đặt:
#include <iostream>
#include <vector>
using namespace std;
// Struct để truy vết
struct Trace
{
int coin; // Chỉ số đồng tiền được thêm vào
int i; // i và j dùng để truy vết trong bảng QHĐ
int j;
Trace(int c = 0, int row = 0, int col = 0)
: coin(c), i(row), j(col) {};
};
const int N = 1e6 + 10;
int n, m, A[N];
vector<int> L, P;
vector<vector<Trace>> d;
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> A[i];
// Quy ước inf = -1
P = vector<int>(m + 1, -1);
L.resize(m + 1);
d = vector<vector<Trace>>(n + 1, vector<Trace>(m + 1));
// Bước QHĐ
for (int i = 1; i <= n; i++)
{
L[0] = 0;
for (int j = 1; j <= m; j++)
if (A[i] > j)
{
L[j] = P[j];
d[i][j] = Trace(0, i - 1, j);
}
else
{
// L[j] = min(P[j], L[j - A[i]]);
// Nếu P[j] và L[j - A[i]] khác inf
if (P[j] != -1 && L[j - A[i]] != -1)
{
if (P[j] < L[j - A[i]] + 1)
{
L[j] = P[j];
d[i][j] = Trace(0, i - 1, j);
}
else
{
L[j] = L[j - A[i]] + 1;
d[i][j] = Trace(i, i, j - A[i]);
}
}
// Chỉ L[j - A[i]] là inf
else if (P[j] != -1)
{
L[j] = P[j];
d[i][j] = Trace(0, i - 1, j);
}
// Chỉ P[j] là inf
else if (L[j - A[i]] != -1)
{
L[j] = L[j - A[i]] + 1;
d[i][j] = Trace(i, i, j - A[i]);
}
// Cả hai số là inf
else
L[j] = -1;
}
P = L;
}
cout << L[m] << '\n';
// Truy vết
if (L[m] != -1)
{
vector<int> cnt(n + 1);
Trace t = d[n][m];
while (t.coin != 0 && t.j != 0)
{
cnt[t.coin]++;
t = d[t.i][t.j];
}
for (int i = 1; i <= n; i++)
cout << cnt[i] << ' ';
}
}3. Nhân ma trận
3.1. Mô hình
Khi nhân một ma trận kích thước $m \times n$ với một ma trận $n \times p$, số phép nhân phải thực hiện là $m \times n \times p$. Mặt khác phép nhân các ma trận có tính kết hợp, tức là: $(A \times B) \times C = A \times (B \times C).$ Do đó khi tính tích nhiều ma trận, ta có thể thực hiện theo các trình tự khác nhau, mỗi trình tự tính sẽ quyết định số phép nhân cần thực hiện. Cho $n+1$ số $d_0,d_1,\ldots,d_n$ và $n$ ma trận $A_1, A_2, …, A_n$, ma trận thứ $i$ có kích thước là $d_{i-1} \times d_i$. Hãy xác định trình tự nhân ma trận $A_1 \times A_2 \times \ldots \times A_n$ sao cho số phép nhân cần thực hiện là ít nhất. Điều kiện: $1\le n\le 300,1\le d_i\le 100$. Input: Số $n$ và $n+1$ số $d_0,d_1,\ldots,d_n$. Output: Số nguyên duy nhất là số phép nhân ít nhất.
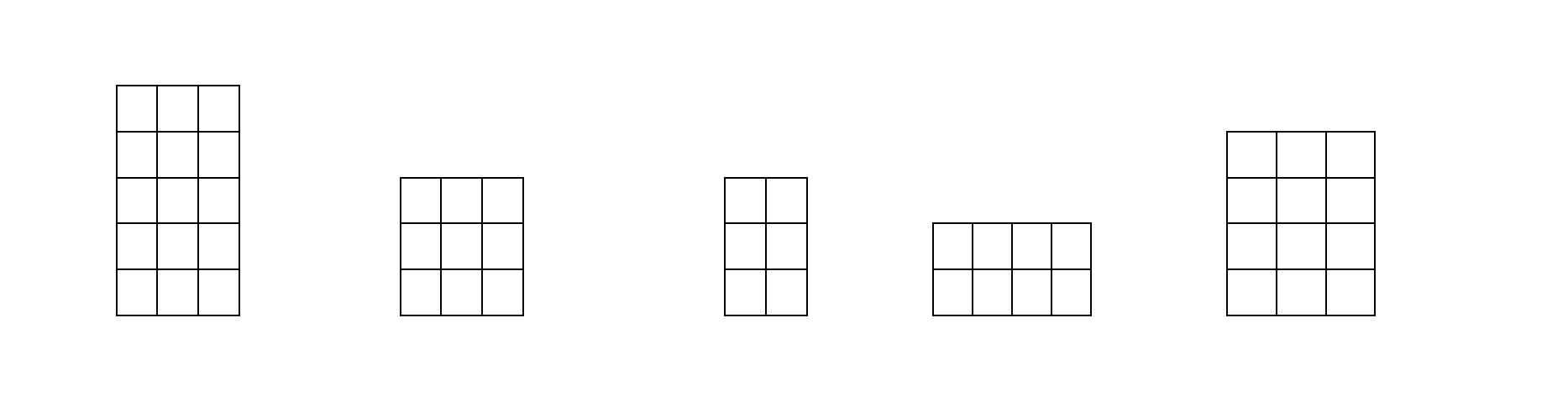
3.2. Lời giải
Gọi $L[i][j]$ là số phép nhân nhỏ nhất cần dùng để tính tích các ma trận từ $A_i$ đến $A_j$ $(A_i \times A_{i+1} \times \ldots \times A_j)$.
Xét tích $(A_i \times A_{i+1} \times \ldots \times A_j)$ với $i<j.$ Khi tính tích trên, phép nhân ma trận cuối cùng sẽ có dạng $B\times C$, sao cho tồn tại một số nguyên $i\le k\le j$ thỏa mãn:
- $B=A_i\times A_{i+1}\times\ldots\times A_k$
- $C=A_{k+1}\times A_{k+1}\times\ldots\times A_j$
Nói cách khác, tích $A_{k+1}\times A_{k+1}\times\ldots\times A_j$ được tính theo trình tự sau: $(A_i \times \ldots \times A_k)\times(A_{k+1}\times\ldots\times A_j)$. Để số phép nhân là nhỏ nhất thì số phép nhân cần dùng khi tính $B$ và $C$ cũng là nhỏ nhất. Giá trị của $L[i][j]$ sẽ là kết quả nhỏ nhất nếu $k$ chạy từ $i$ đến $j-1$. Từ đó, ta có công thức truy hồi như sau:
- $L[i][i]=0$
- $L[i][j] = \min(L[i][k] + L[k+1][j] + d_{i-1}\times d_{k}\times d_j)$, trong đó $i\le k < j,$ nếu $i<j$
3.3. Code tham khảo
Để tính các giá trị $L[i][j]$, ta có thể dùng hai cách: đệ quy có nhớ và tính theo thứ tự.
Nếu tính theo thứ tự, để tính được $L[i][j]$ ta cần các giá trị $L[i][k]$ và $L[k+1][j]$ sao cho $i\le k<j$. Do đó, không thể tính $L[i][j]$ theo thứ tự tăng dần của $i$ hoặc $j$. Thay vào đó, ta sẽ tính theo thứ tự tăng dần của $j-i$ như sau: đầu tiên tính các số $L[i][j]$ thỏa mãn $j-i=0$, sau đó tính giá trị các số tiếp theo với $j-i=1;2;\ldots;n-1$. Như vậy, khi tính $L[i][j]$ thì các giá trị $L[i][k],L[k+1][j]$ đã được tính, với $i\le k < j$.
Đệ quy có nhớ:
#include <iostream>
using namespace std;
const int N = 310;
int d[N], L[N][N], n;
int calc(int i, int j)
{
if (L[i][j] == -1)
{
if (i == j)
L[i][j] = 0;
else
{
L[i][j] = calc(i + 1, j) + d[i - 1] * d[i] * d[j];
for (int k = i; k < j; k++)
L[i][j] = min(L[i][j], calc(i, k) + calc(k + 1, j) + d[i - 1] * d[k] * d[j]);
}
}
return L[i][j];
}
int main()
{
cin >> n;
for (int i = 0; i <= n; i++)
cin >> d[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
L[i][j] = -1;
cout << calc(1, n);
}#include <iostream>
using namespace std;
const int N = 310;
int d[N], L[N][N], n;
int main()
{
cin >> n;
for (int i = 0; i <= n; i++)
cin >> d[i];
for (int dis = 1; dis < n; dis++)
for (int i = 1; i + dis <= n; i++)
{
int j = i + dis;
L[i][j] = L[i + 1][j] + d[i - 1] * d[i] * d[j];
for (int k = i; k < j; k++)
L[i][j] = min(L[i][j], L[i][k] + L[k + 1][j] + d[i - 1] * d[k] * d[j]);
}
cout << L[1][n];
}3.4. Một số bài toán khác
3.4.1. Chia đa giác
Cho một đa giác lồi $n$ đỉnh được đánh số từ $1$ đến $n$ theo chiều kim đồng hồ. Bằng các đường chéo không cắt nhau, ta có thể chia đa giác thành $n-2$ tam giác. Hãy xác định cách chia có tổng các đường chéo ngắn nhất. Điều kiện: $4\le n\le 300,-10^6\le x_i,y_i\le 10^6$ (với $(x_i,y_i)$ là tọa độ của đỉnh thứ $i$). Input: Một số tự nhiên $n$ và $n$ bộ $(x_i,y_i)$. Output: In ra tổng các đường chéo của cách chia ngắn nhất.
Lời giải:
Để đơn giản ta coi mọi đoạn thẳng nối hai đỉnh bất kì đều là “đường chéo” (nếu nối hai đỉnh trùng nhau hoặc hai đỉnh liên tiếp thì có độ dài bằng $0$).
Gọi $L[i][j], (i\le j)$ là tổng độ dài bé nhất có thể của các đường chéo dùng để chia đa giác gồm các đỉnh từ $i$ đến $j$ thành các tam giác.
- Nếu $j<i+3$ thì đa giác đó có ít hơn 4 đỉnh, không cần phải chia nên $L[i][j]=0$.
- Ngược lại ta xét cách chia đa giác đó bằng cách chọn một đỉnh $k$ nằm giữa $i$, $j$ và nối $i$, $j$ với $k$. Khi đó $L[i][j]=L[i][k]+L[k][j]+d(i,k)+d(k,j)$ với $d(x,y)$ là độ dài đường chéo nối đỉnh $x$ với đỉnh $y$.
Từ đó, ta rút ra công thức truy hồi sau:
- $L[i][j]=0$ nếu $i\le j<i+3$
- $L[i][j]=\min(L[i][k]+L[k][j]+d(i,k)+d(k,j))$ với $k=i+1,…j-1$, nếu $j\ge i+3$
$L[1][n]$ là tổng đường chéo của cách chia tối ưu.
Cài đặt:
#include <iostream>
#include <cmath>
using namespace std;
struct Point
{
double x;
double y;
Point(double xx = 0.0, double yy = 0.0)
: x(xx), y(yy) {};
};
double distance(const Point& a, const Point& b)
{
return sqrtl((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
const int N = 310;
int n;
double L[N][N];
Point p[N];
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> p[i].x >> p[i].y;
for (int dis = 3; dis <= n - 1; dis++)
for (int i = 1; i + dis <= n; i++)
{
int j = i + dis;
L[i][j] = L[i + 1][j] + distance(p[i + 1], p[j]);
for (int k = i + 1; k <= j - 1; k++)
L[i][j] = min(L[i][j], L[i][k] + L[k][j] + distance(p[i], p[k]) + distance(p[k], p[j]));
}
cout << L[1][n];
}3.4.2. Biểu thức số học
Cho $n$ số thực không âm $A_1,A_2,\ldots,A_n$ được viết thành một hàng ngang theo thứ tự đó. Giữa hai số liên tiếp có một dấu
+hoặc*cho trước. Hãy đặt các dấu ngoặc vào biểu thức để giá trị thu được là lớn nhất. Điều kiện: $1\le n \le 300$.
Lời giải:
Giả sử biểu thức ban đầu là $A_1\cdot A_2\cdot\ldots\cdot A_n$, trong đó $\cdot$ là + hoặc * theo đề bài.
Gọi $L[i,j]$ là giá trị lớn nhất có thể có của biểu thức $A_i \cdot A_{i+1} \cdot … \cdot A_j$.
- Nếu $i=j$ thì $L[i][j]=A_i$
- Nếu $j>i$ thì có thể tính biểu thức $A_i \cdot A_{i+1} \cdot … \cdot A_j$ bằng cách chia thành 2 nhóm: $(A_i \cdot A_{i+1} \cdot … \cdot A_k) \cdot (A_{k+1} \cdot … \cdot A_j)(i\le k <j)$ (lập luận tương tự như bài toán nhân ma trận). Do $A_i\ge 0$ nên để $L[i,j]$ lớn nhất thì cách đặt ngoặc của hai biểu thức con cũng tối ưu. Khi đó $L[i][j]=L[i][k] \cdot L[k+1][j]$, trong đó $i\le k <j$ và $\cdot$ là phép toán giữa $A_k$ và $A_{k+1}$.
Vậy ta có công thức truy hồi như sau:
- $L[i][i]=A_i$
- $L[i][j]=\max(L[i][k] \cdot L[k+1][j])$ với $i\le k <j$
4. Ghép cặp
4.1. Mô hình
Có $n$ lọ hoa sắp thành một hàng ngang và $k$ bó hoa được đánh số thứ tự từ $1$ đến $k$. Cần cắm $k$ bó hoa trên vào $n$ lọ sao cho hoa có số thứ tự nhỏ phải đứng trước hoa có số thứ tự lớn. Giá trị thẩm mỹ tương ứng khi cắm hoa $i$ vào lọ thứ $j$ là $v_{i,j}\ge0$. Hãy tìm một cách cắm sao cho tổng giá trị thẫm mỹ là lớn nhất. Chú ý rằng mỗi bó hoa phải được cắm vào một lọ và mỗi lọ cũng chỉ cắm tối đa một bó hoa. Điều kiện: $1\le n \times k\le10^6,1\le v_{i,j}\le10^9$.
4.2. Lời giải
Nhận xét rằng bài toán nêu trên là một bài toán ghép cặp có yêu cầu về thứ tự nên ta có thể giải quyết bằng phương pháp QHĐ.
Trạng thái của bài toán phụ thuộc vào hai yếu tố: số bông hoa đang được xét và số lọ hoa đang dùng. Ta có thể gọi $L[i][j]$ là tổng giá trị thẩm mỹ lớn nhất khi cắm hoa $1$ đến hoa $j$ dùng $i$ lọ đầu tiên. Khi đó:
- Nếu $i = j$: chỉ có một cách cắm, nên $L[i][i] = \sum_{k=1}^iv_{k,k}$
- Nếu $i < j$: không thể cắm $j$ hoa vào $i$ lọ
- Nếu $i > j$: ta có thể cắm hoa thứ $j$ vào lọ $i$ hoặc các lọ trước đó. Do đó có hai trường hợp:
- Nếu hoa $j$ được cắm vào lọ $i$: khi đó cách cắm $j-1$ hoa vào $i-1$ lọ trước đó cũng phải có tổng giá trị thẩm mỹ lớn nhất. Do đó $L[i][j] = L[i-1][j-1]+v_{i,j}$
- Không cắm hoa $j$ vào lọ $i$ (cắm vào lọ trước $i$), giá trị thẫm mỹ của cách cắm là $L[i][j] = L[i - 1][j]$
Tóm lại, công thức truy hồi của bài toán là:
- $L[0][j]=L[i][0]=0$
- $L[i][i] = \sum_{k=1}^iv_{k,k}$
- $L[i][j] = \max(L[i - 1][j - 1] + v_{i,j},L[i - 1][j])$ nếu $i>j$
Đáp án của bài toán là $L[n][k]$.
Nhận xét:
- Ta chỉ cần điều kiện $1$ và $3$ vì điều kiện $2$ có thể được suy ra trực tiếp từ hai điều kiện trên.
- Công thức QHĐ của bài này không có gì đặc biệt một khi ta tìm ra trạng thái của bài toán.
4.3. Code tham khảo
Tương tự các bài toán trước, có hai phương pháp cài đặt QHĐ, với phương pháp tính từng hàng cài đặt nhanh và tiết kiệm hơn:
vector<int> P(k + 1), L(k + 1);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
{
L[j] = max(P[j - 1] + v[i][j], P[j]);
}
P = L;
}
cout << L[k];4.4. Một số bài toán khác
4.4.1. Xếp phòng học
Một trường học có $n$ phòng học đánh số từ $1$ đến $n$ và $k$ nhóm học sinh đánh số từ $1$ đến $k$. Cần xếp $k$ nhóm học sinh vào các phòng học khác nhau sao cho với hai nhóm $i<j$ có $a, b$ lần lượt là phòng học của hai nhóm thì $a<b$. Nói cách khác, nhóm có số hiệu lớn hơn sẽ được ưu tiên phòng có số hiệu lớn hơn. Nếu phòng học nào đó có chứa học sinh thì số ghế thừa phải được chuyển ra ngoài, nếu thiếu ghế thì phải lấy thêm. Biết số ghế có sẵn trong phòng thứ $i$ là $A_i$ và số học sinh nhóm thứ $j$ là $B_j(1\le i \le n,1\le j \le k).$ Tính số lần chuyển ghế ra vào ít nhất có thể. Điều kiện: $1\le n\times k\le10^6, 1\le A_i,B_j\le10^9$.
Lời giải:
Khi xếp nhóm $i$ vào phòng $j$ thì số lần chuyển ghế chính là độ chênh lệch giữa số ghế trong phòng $i$ và số học sinh trong nhóm. Khi đó, "giá trị thẩm mỹ" nếu lớp $j$ học ở phòng $i$ là $v_{i,j}=\lvert A_i - B_j \rvert$. Ta cần tìm cách ghép $k$ nhóm học sinh với $n$ lớp học sao cho nhóm có số hiệu nhỏ hơn thì học lớp có số hiệu nhỏ hơn. Để ý trong bài toán này, tổng giá trị thẩm mỹ của cách ghép phải là nhỏ nhất.
4.4.2. Mua giày (Đề QG bảng B năm 2003)
Có $n$ đôi giày, đôi giày thứ $i$ có kích thước $H_i$. Có $k$ người cần mua giày, người thứ $j$ cần mua đôi giày kích thước $S_j$. Khi người $i$ chọn mua đôi giày $j$ thì độ lệch sẽ là $|H_i-S_j|$. Hãy tìm cách chọn mua giày cho $k$ người trên sao cho tổng độ lệch là ít nhất. Biết rằng mỗi người chỉ mua 1 đôi giày và 1 đôi giày cũng chỉ có tối đa một người mua. Điều kiện: $1\le n\times k\le10^6, 1\le H_i,S_j\le10^9$.
Lời giải:
Bài này khác với bài Xếp phòng học ở trên ở chỗ: người có thứ tự nhỏ hơn không nhất thiết phải mua đôi giày thứ tự nhỏ hơn.
Tuy nhiên, để đưa bài toán về dạng ghép cặp, ta có nhận xét sau:
Cho $2$ dãy số nguyên dương sắp thứ tự $A_1\le A_2\le\ldots\le A_n$ và $B_1\le B_2\le\ldots\le B_n$. Gọi $C_1,C_2,\ldots,C_n$ là một hoán vị của $B_1,B_2,\ldots,B_n$. Khi đó: $|A_1-B_1|+|A_2-B_2|+\ldots+|A_n-B_n|\le|A_1-C_1|+|A_2-C_2|+\ldots+|A_n-C_n|$
Chứng minh:
Gọi $P=(P_1,P_2,\ldots,P_n)$ là một hoán vị của $B_1,B_2,\ldots,B_n$. Ta đặt: $f(P)=|A_1-P_1|+|A_2-P_2|+\ldots+|A_n-P_n|$. Giả sử trong hoán vị P tồn tại một nghịch thế $u,v$, tức là $u<v$ và $P_u\ge P_v.$ Đặt $P'=P_1,P_2,\ldots,P_{u-1},P_v,P_{u+1},\ldots,P_{v-1},P_u,P_{v+1},\ldots,P_n$.
Xét hiệu:
\begin{align}
f(P)-f(P') & = |A_u-P_u|+|A_v-P_v|-|A_u-P_v|-|A_v-P_u|
\end{align}
Trường hợp 1: $P_u\ge A_v\ge A_u$, ta có:
\begin{align}
f(P)-f(P') & = P_u-A_u+|A_v-P_v|-|A_u-P_v|-P_u+A_v
&= |A_v-A_u|+|A_v-P_v|-|A_u-P_v|
&\ge0
\end{align}
Trường hợp 2: $A_v> P_u\ge P_v$, ta có:
\begin{align}
f(P)-f(P') & = |A_u-P_u|+A_v-P_v-|A_u-P_v|-A_v+P_u
&= |A_v-P_u|+|P_u-P_v|-|A_u-P_v|
&\ge0
\end{align}
Do đó ta luôn có $f(P')\le f(P)$. Từ đó suy ra với một hoán vị $P$ khác $B_1,B_2,\ldots,B_n$, ta luôn có thể đổi chỗ hai số hạng trong một cặp nghịch thế của $P$ để được một hoán vị $P'$ có giá trị $f(P')\le f(P)$. Suy ra $f(P)$ đạt $\min$ khi $P$ là $B_1,B_2,\ldots,B_n.$ Đến đây ta chứng minh được mệnh đề trên.
Trở lại bài toán gốc, nếu ta sắp xếp các đôi giày và các người mua giày theo trình tự cỡ giày tăng dần, từ nhận xét đã chứng minh ta suy ra tổng độ lệch là nhỏ nhất khi người cần cỡ giày nhỏ hơn mua chiếc giày nhỏ hơn. Đến đây, bài toán giống với bài toán gốc và có thể giải bằng phương pháp QHĐ.
Kết
Điều khó nhất để giải một bài toán quy hoạch động là biết rằng đó là một bài toán QHĐ và tìm được công thức/trạng thái của nó. Việc mò mẫm từ đầu không hề dễ dàng, nhưng nếu ta đưa được bài toán cần giải về một bài toán QHĐ kinh điển đã biết thì việc xử lý sẽ đơn giản hơn nhiều. Do đó, tìm hiểu mô hình, công thức và cách cài đặt những bài toán QHĐ kinh điển là một việc rất cần thiết. Hi vọng trong bài viết này, các bạn đã tìm hiểu thêm được một số bài tập kinh điển cũng như các biến thể của chúng.