Quy hoạch động cơ bản (Phần 1)

Quy hoạch động cơ bản (Phần 1)

Bài viết có tham khảo và bổ sung, chỉnh sửa từ TopCoder và một số nguồn khác.

Người viết: Nguyễn Anh Bảo - Đại học Bách Khoa Hà Nội

Reviewer:

  • Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên, ĐHQG-HCM
  • Ngô Nhật Quang - Trường THPT chuyên Khoa học Tự Nhiên, ĐHQGHN

Table of Contents

Giới thiệu

Quy hoạch động (QHĐ) (Dynamic Programming) là một trong những kĩ thuật quan trọng và cơ bản nhất trong lập trình thi đấu. Bài viết này sẽ trình bày và giải thích các khái niệm liên quan đến quy hoạch động đồng thời đưa ra các ví dụ minh họa.

Beginner

Để mở đầu, ta xét ví dụ sau:

Ví dụ 1

Bạn An có $n$ chiếc ghế màu trắng, $n$ chiếc ghế màu đen và $n$ chiếc ghế màu đỏ. An muốn chọn ra $n$ chiếc ghế để xếp thành một hàng ngang. Do An không thích màu đỏ nên An không muốn xếp hai chiếc ghế đỏ cạnh nhau. Tính số cách xếp ghế thỏa mãn điều kiện đó. Điều kiện: $1\le n\le 10^5$.

Lưu ý: hai cách xếp được xem là khác nhau khi tồn tại một vị trí mà hai cách có hai loại ghế khác nhau.

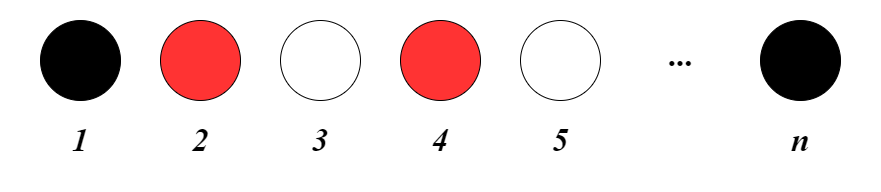
Bây giờ ta sẽ xây dựng thuật giải:

Thuật toán đệ quy

Gọi số cách xếp $i$ cái ghế là $f[i]$. Ta xét chiếc ghế thứ $n$.

  • Nếu nó có màu đen hoặc trắng thì chiếc ghế cạnh nó có thể có một trong ba màu. Do đó ta chỉ cần bố trí $n-1$ chiếc ghế còn lại thỏa mãn yêu cầu. Do có 2 cách chọn màu cho ghế thứ $n$ và $f[n-1]$ cách chọn màu cho các ghế còn lại nên số cách xếp trong trường hợp này là $2 * f[n-1]$.

  • Nếu nó có màu đỏ thì chiếc ghế cạnh nó chỉ có thể có màu trắng hoặc đen. Do vậy nên chiếc ghế thứ $n-2$ có thể có một trong ba màu. Khi đó ta cũng chỉ cần bố trí $n-2$ chiếc ghế còn lại thỏa mãn yêu cầu. Số cách xếp trong trường hợp này là $1* 2* f[n-2]$.

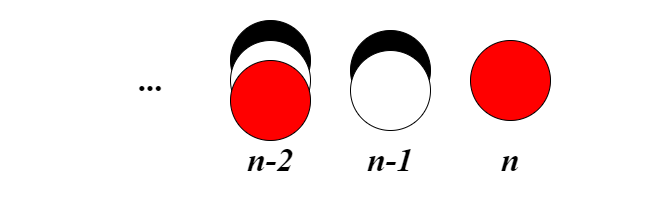
Với ý tưởng trên, ta có thể giải bài toán này như các bài toán đệ quy đơn giản. Cài đặt như sau:

// Tính số cách sắp xếp n cái ghế
int solve(int n)
{
    // Trường hợp cơ bản
    if (n == 1)
        return 3;
    if (n == 2)
        return 8;
    // Bước đệ quy
    return 2 * solve(n - 1) + 2 * solve(n - 2);
}
Thuật toán trên có độ phức tạp lũy thừa nên chỉ áp dụng được với $n$ nhỏ $(n < 45)$, không đủ nhanh so với yêu cầu bài toán.

Tối ưu thuật toán đệ quy

Thuật toán trên chạy chậm vì một số hàm solve(i) được gọi rất nhiều lần. Ta lấy ví dụ sau:

Giả sử cần tính solve(1000). Khi đó cần tính solve(999) và solve(998).

Để tính solve(999) cần gọi hàm solve(998) và solve(997). Để tính solve(998) cần gọi hàm solve(997) và solve(996). Để tính solve(997) cần gọi hàm solve(996) và solve(995). $\ldots$ Ta có thể biểu diễn các hàm được gọi bằng một sơ đồ như sau:

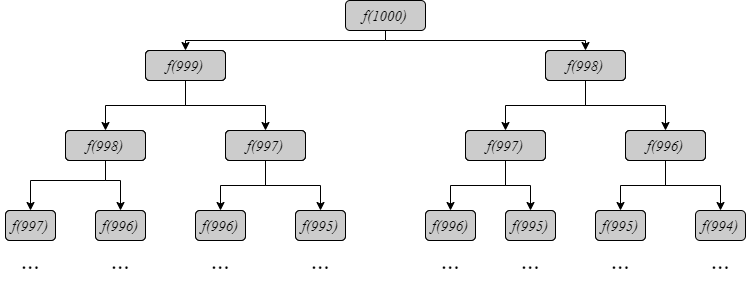
Từ sơ đồ trên ta thấy có nhiều hàm bị gọi rất nhiều lần một cách không cần thiết:

  • solve(998) được gọi $2$ lần
  • solve(997) được gọi $3$ lần
  • solve(996) được gọi $5$ lần
  • $\ldots$

Để khắc phục điều này ta có thể sử dụng một mảng nhớ $d$ sao cho $d[i]$ là giá trị của solve(i):

int d[100010];

int solve(int n)
{
    if (n == 1)
        return 3;
    else if (n == 2)
        return 8;
    else if (d[n] != 0)
        return d[n];
    else
    {
        d[n] = 2 * f(n - 1) + 2 * f(n - 2);
        return d[n];
    }
}
Thuật toán trên có độ phức tạp $O(n)$.

Với cách tiếp cận trên, ta quan tâm đến giá trị cuối cùng $f[n]$, sau đó mới xem xét những giá trị bé hơn cần thiết cho tính toán.

Nhưng với phương pháp quy hoạch động, ta sẽ quan tâm đến các bài toán với tham số nhỏ hơn trước tiên.

Phương pháp tiếp cận

Khi nào có thể áp dụng QHĐ

Quy hoạch động được sử dụng khi ta tìm được công thức liên hệ giữa kết quả bài toán có đầu vào cho trước với một (hoặc một số) bài toán con tương tự nhưng có đầu vào nhỏ hơn. Khi ta biết được một số trạng thái bắt đầu của bài toán, nói cách khác - bài toán con với những đầu vào rất nhỏ, ta có thể sử dụng QHĐ để tính ra kết quả cuối cùng.

Trạng thái của bài toán là gì?

Trạng thái là một trường hợp, một bài toán con của bài toán lớn với tham số cho trước.

Ví dụ, trạng thái trong bài này là số cách sắp xếp $n$ chiếc ghế thỏa mãn không có hai ghế đỏ cạnh nhau.

Liên hệ giữa các trạng thái

Để giải bài toán quy hoạch động, điều quan trọng nhất là tìm ra mối liên hệ giữa một trạng thái và các trạng thái có tham số nhỏ hơn.

Gọi $f[i]$ là cách sắp xếp $i$ chiếc ghế thành một hàng dọc. Khi đó ta có:

\begin{cases} f[1] = 3; f[2] = 8 \newline f[i] = 2f[i - 1] + 2f[i - 2], \forall i=3;4;\ldots;n(*) \end{cases}

Công thức $(*)$ được gọi là công thức truy hồi.

Tìm kết quả cuối cùng

Sau khi đã biết công thức truy hồi và tính được $f[1]$, $f[2]$, ta có thể tìm $f[n]$.

Code mẫu:

#include <iostream>
using namespace std;

long long n, f[100010];

int main()
{
    cin >> n;
    f[1] = 3;
    f[2] = 8;
    for (int i = 3; i <= n; i++)
        f[i] = 2 * f[i - 1] + 2 * f[i - 2];
    cout << f[n];
    return 0;
}
Độ phức tạp của thuật toán trên là $O(n)$, nhưng cách thực hiện đơn giản hơn đệ quy có nhớ.

Phân tích: Từ ví dụ trên, ta thấy phương pháp QHĐ được triển khai theo các bước sau:

  • Xác định trạng thái của bài toán
  • Tìm mối liên hệ giữa các trạng thái (tìm công thức truy hồi)
  • Khởi tạo các giá trị ban đầu và cài đặt công thức truy hồi

Ta tiếp tục với ví dụ tiếp theo:

Ví dụ 2

Cho $N$ loại đồng xu và giá tiền của mỗi loại là các số nguyên $v_1,v_2,\ldots,v_n$, và số nguyên dương $S$. Tìm số đồng xu nhỏ nhất để tổng giá trị của chúng bằng $S$ (số lượng đồng xu không giới hạn), nếu không tồn tại một số đồng xu có tổng là $S$ thì in ra $-1$. Điều kiện: $1\le S,N\le1000$ và $1\le v_1,v_2,\dots,v_n\le S$.

Ta xây dựng thuật toán QHĐ:

Trạng thái của bài toán là số đồng xu nhỏ nhất có tổng giá tiền là $i$. Ta sẽ dùng mảng $f[i]$ để lưu số đồng xu ít nhất có tổng giá trị là $i$, nếu không tồn tại các đồng xu có tổng là $i$ thì gán $f[i] = -1$.

Cần một công thức truy hồi để tính $f[i]$ theo $f[1],f[2],\ldots,f[i-1]$.

Để ý thấy với $i$ bất kì, nếu có một đồng xu giá trị $v_j \le i$ thì ta có thể thêm đồng đó vào các đồng có tổng giá trị là $i-v_j$. Giả sử $m$ là số đồng xu ít nhất có tổng là $i-v_j$, khi đó có $m+1$ đồng xu có tổng giá trị $i$. Nếu $f[i] = -1$ thì ta cập nhật $f[i] = m + 1$, nếu $f[i] \ne -1$ thì $f[i]=\min(f[i], m+1)$.

Sau đây là ví dụ: Cho các đồng xu với giá tiền $1,3,5$. Và $S = 11$.

Đầu tiên, ta bắt đầu từ trạng thái cơ bản nhất: $f[0]=0$.

Xét đến tổng $1$. Có duy nhất đồng xu $1$ nhỏ hơn hoặc bằng tổng $1$, nên ta có $f[1]=f[1−v_1]+1=f[0]+1=1$.

Xét đến tổng $2$. Cũng giống như tổng trước, chỉ có $1$ đổng xu không vượt quá $2$, suy ra $f[2]=f[2−v_1]+1=f[1]+1=2$.

Đến tổng $3$. Lần này có hai đồng xu không vượt quá $3$ là $1$ và $3$. Nếu ta chọn đồng $1$, ta có $f[3]=f[3−v_1]+1=f[2]+1=3$; nếu ta chọn đồng $3$, ta có $f[3]=f[3−v_2]+1=f[0]+1=1$. Rõ ràng $1 ≤ 3$ nên ta chọn đồng $3$ và $f[3]=1$.

Xét tiếp đến tổng $4,$ tổng $5,\ldots$ đến $11$ bằng cách như trên.

Đây là lời giải cho tất cả các tổng:

Tổng Lượng xu nhỏ nhất Xu được chọn
(Tổng còn lại)
$0$ $0$ -
$1$ $1$ $1 (0)$
$2$ $2$ $1 (1)$
$3$ $1$ $3 (0)$
$4$ $2$ $1 (3)$
$5$ $1$ $5 (0)$
$6$ $2$ $3 (3)$
$7$ $3$ $1 (6)$
$8$ $2$ $3 (5)$
$9$ $3$ $1 (8)$
$10$ $2$ $5 (5)$
$11$ $3$ $1 (10)$

Code tham khảo:

#include <iostream>
using namespace std;

const int N = 1e3 + 10;
int f[N], v[N], n, S;
// Gán f[i] = -1 nếu không thể tìm được một số đồng xu tổng bằng i

int main()
{
    cin >> n >> S;
    for (int i = 1; i <= n; i++)
        cin >> v[i];

    for (int i = 1; i <= S; i++)
        f[i] = -1;

    for (int i = 1; i <= S; i++)
        for (int j = 1; j <= n; j++)
            if (v[j] <= i && f[i - v[j]] != -1)
                {
                    if (f[i] != -1)
                        f[i] = min(f[i], f[i - v[j]] + 1);
                    else
                        f[i] = f[i - v[j]] + 1;
                }
    cout << f[S];
}
Nhận xét: Đôi khi, trạng thái trong bài QHĐ chính là yêu cầu của bài toán.

Tìm độ dài dãy con không giảm dài nhất

Phần này giới thiệu một lớp bài toán QHĐ điển hình. Ta bắt đầu bằng bài toán sau:

Cho dãy số nguyên dương $a_1,a_2,\ldots,a_n$. Tìm độ dài của dãy con không giảm dài nhất của dãy. Dãy con của một dãy là dãy số thu được bằng cách bỏ đi một số phần tử của dãy ban đầu. Điều kiện: $1\le n\le 1000$ và $1\le a_1,a_2,\dots,a_n\le 10^9$.

Đầu tiên cần xác định trạng thái của bài toán.

Ta đặt $f[i]$ là độ dài của dãy con không giảm dài nhất kết thúc ở $a_i$. $f[i]$ là trạng thái của bài toán. Ta khởi tạo $f[i] = 1$ ($a_i$ là một dãy không giảm).

Với $j<i$ mà $a_j \ge a_i$ thì ta có thể thêm $a_i$ vào dãy không giảm kết thúc ở $a_j$, do đó nếu $f[j] + 1$ lớn hơn giá trị hiện tại của $f[i]$ thì ta cập nhật $f[i] = f[j] + 1$.

Cuối cùng để tìm được độ dài dãy con không giảm dài nhất ta tính $\max (f[1],f[2],\ldots,f[n])$.

Code tham khảo

#include <iostream>
using namespace std;

const int N = 1e3 + 10;
int f[N], a[N], n;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i <= n; i++)
        f[i] = 1;
    for (int i = 2; i <= n; i++)
        for (int j = 1; j < i; j++)
            if (a[j] <= a[i])
                f[i] = max(f[i], f[j] + 1);
    int mx = f[1];
    for (int i = 2; i <= n; i++)
        mx = max(mx, f[i]);
    cout << mx;
}

Ví dụ minh họa:

$i$ $1$ $2$ $3$ $4$ $5$
$a[i]$ $1$ $4$ $2$ $3$ $7$
$f[i]$ $1$ $f[1]+1=2$ $f[1]+1=2$ $f[3]+1=3$ $f[4]+1=4$

Nhận xét: Một số bài QHĐ có trạng thái là yêu cầu bài toán với $i$ phần tử đầu tiên của dãy số.

Bài toán tìm dãy con không giảm dài nhất là một ví dụ điển hình của phương pháp QHĐ. Một số biến thể của bài toán này tạo thành một lớp các bài toán tương tự nhau. Các bài toán đó có một số tính chất đặc trưng sau:

  • Mỗi phần tử $a_i$ xuất hiện tối đa một lần trong dãy con. Vì vậy ta sẽ dùng vòng For duyệt qua các phần tử $a_i$ trong dãy.
  • Thứ tự của các phần tử được chọn phải được giữ nguyên so với dãy ban đầu.

Một số biến thể:

Tìm dãy con không giảm dài nhất

Bài toán giống ví dụ 3, nhưng yêu cầu in ra dãy con đó. Ta có thể làm tương tự như trên, nhưng thêm mảng truy vết $d[i]$ lưu vị trí $j<i$ mà $f[i]=f[j]+1$. Ta có thể cài đặt như sau:

#include <iostream>
#include <vector>
using namespace std;

const int N = 1e3 + 10;
int f[N], a[N], d[N], n;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    // Bước QHĐ
    for (int i = 1; i <= n; i++)
    {
        f[i] = 1;
        for (int j = 1; j < i; j++)
            if (a[j] <= a[i] && f[i] < f[j] + 1)
            {
                f[i] = f[j] + 1;
                d[i] = j;
            }
    }
    // Tìm t là vị trí cuối cùng của dãy dài nhất
    int t = 1;
    for (int i = 1; i <= n; i++)
        if (f[i] > f[t])
            t = i;
    // In ra dãy con đó
    vector<int> seq;
    while (t)
    {
        seq.push_back(a[t]);
        t = d[t];
    }
    for (auto i = seq.rbegin(); i != seq.rend(); i++)
        cout << (*i) << ' ';
}

Bố trí phòng họp (mất tính thứ tự so với dãy ban đầu)

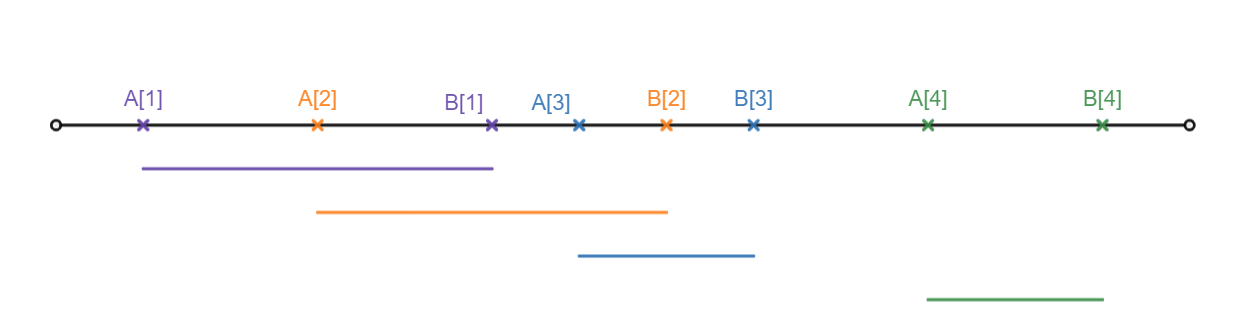
Có $n$ cuộc họp, cuộc họp thứ $i$ bắt đầu vào thời điểm $A_i$ và kết thúc ở thời điểm $B_i$. Do chỉ có một phòng hội thảo nên 2 cuộc họp bất kì sẽ được cùng bố trí phục vụ nếu khoảng thời gian làm việc của chúng chỉ giao nhau tại đầu mút hoặc không giao nhau. Hãy bố trí phòng họp để phục vụ được nhiều cuộc họp nhất. Điều kiện: $1\le n\le1000$ và $1\le A_i\le B_i\le10^9$ với mọi $i=1;2;\dots;n$. Input: Số nguyên $n$ và $n$ dòng tiếp theo có dòng thứ $i$ là thời điểm bắt đầu $A_i$ và kết thúc $B_i$ của cuộc họp thứ $i$. Output: một dòng gồm số thứ tự ban đầu của các cuộc họp được bố trí, theo thứ tự thời gian.

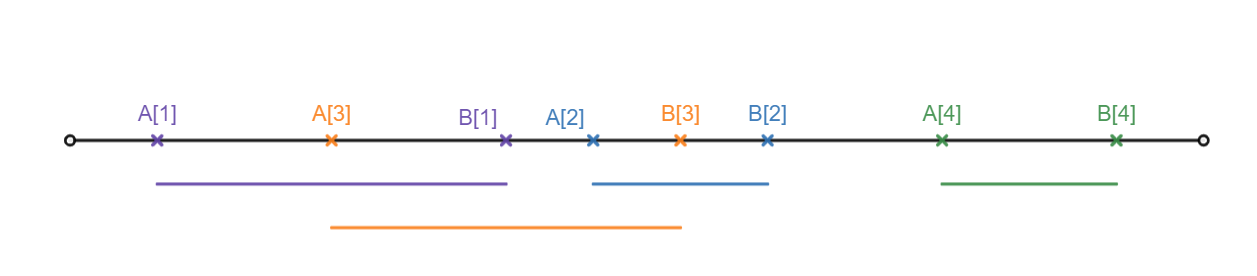Hướng dẫn:

Sắp xếp các cuộc họp tăng dần theo thời điểm bắt đầu $A_i$. Thế thì cuộc họp $i$ sẽ bố trí được sau cuộc họp $j$ khi và chỉ khi $j<i$ và $B_j \le A_i$. Yêu cầu bố trí được nhiều cuộc họp nhất có thể đưa về việc tìm dãy các cuộc họp dài nhất thoả mãn điều kiện trên.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct Meeting
{
    Meeting(int aa = 1, int bb = 1, int nn = 1)
    : a(aa), b(bb), num(nn)
    { };
    int a; // Thời điểm bắt đầu cuộc họp
    int b; // Thời điểm kết thúc cuộc họp
    int num; // Số thứ tự của cuộc họp
};

const int N = 1e3 + 10;
int n, f[N], d[N];
Meeting m[N];

// Hàm so sánh để sắp xếp
bool compare(const Meeting& x, const Meeting& y)
{
    return x.a < y.a || (x.a == y.a && x.b < y.b);
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        m[i].num = i;
        cin >> m[i].a >> m[i].b;
    }
    sort(m + 1, m + n + 1, compare);
    // Bước quy hoạch động
    for (int i = 1; i <= n; i++)
    {
        f[i] = 1;
        for (int j = 1; j < i; j++)
            if (m[j].b <= m[i].a && f[i] < f[j] + 1)
            {
                f[i] = f[j] + 1;
                d[i] = j;
            }
    }
    // Truy vết
    int t = 1;
    for (int i = 1; i <= n; i++)
        if (f[i] > f[t])
            t = i;
    vector<int> seq;
    while (t)
    {
        seq.push_back(m[t].num);
        t = d[t];
    }
    for (auto i = seq.rbegin(); i != seq.rend(); i++)
        cout << (*i) << ' ';
}

Cho thuê máy

Trung tâm tính toán hiệu năng cao nhận được đơn đặt hàng của $n$ khách hàng. Khách hàng $i$ muốn sử dụng máy trong khoảng thời gian từ $a_i$ đến $b_i$ và trả tiền thuê là $c_i$. Hãy bố trí lịch thuê máy để tổng số tiền thu được là lớn nhất mà thời gian sử dụng máy của 2 khách hàng bất kì được phục vụ đều không giao nhau (cả trung tâm chỉ có một máy cho thuê). Điều kiện: $1\le n\le1000$ và $1\le A_i\le B_i\le10^9, 1\le c_i\le10^6$ với mọi $i=1;2;\dots;n$.

Hướng dẫn:

Tương tự như bài toán bố trí phòng họp, nếu sắp xếp các đơn đặt hàng theo thời điểm bắt đầu, ta sẽ đưa được về bài toán tìm dãy con có tổng lớn nhất. Bài toán này là biến thể của bài toán tìm dãy con tăng dài nhất, ta có thể cài đặt bằng đoạn chương trình như sau:

struct Value
{
    Value(int aa = 1, int bb = 1, int cc = 1, int nn = 1)
    : a(aa), b(bb), num(nn)
    { };
    int a; // Thời điểm bắt đầu thuê
    int b; // Thời điểm kết thúc thuê
    int c; // Tiền thuê
    int num; // Số thứ tự
}

const int N = 1e3 + 10;
int n, f[N], d[N];
Value m[N];

bool compare(const Value& x, const Value& y)
{
    return x.a < y.a || (x.a == y.a && x.b < y.b);
}
int main()
{
    // ...
    sort(m + 1, m + n + 1, compare);
    // Bước quy hoạch động
    for (int i = 1; i <= n; i++)
    {
        f[i] = m[i].c;
        for (int j = 1; j < i; j++)
            if (m[j].b <= m[i].a && f[i] < f[j] + m[i].c)
            {
                f[i] = f[j] + m[i].c;
                d[i] = j;
            }
    }
    // ... truy vết
}

Dãy tam giác bao nhau

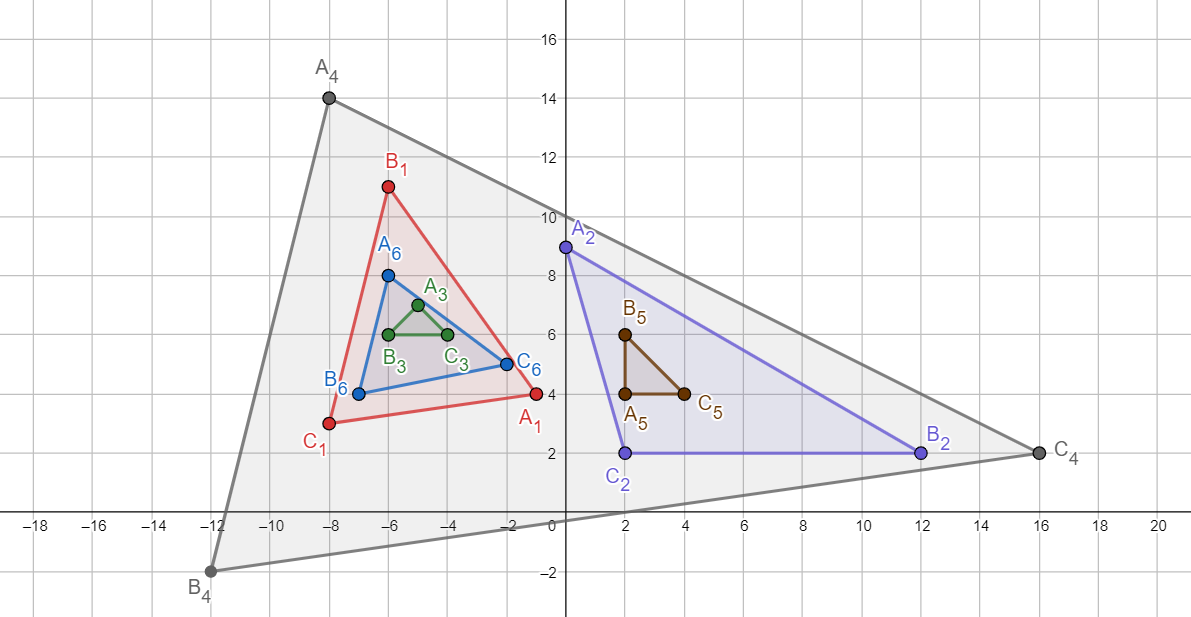
Cho $n$ tam giác trên mặt phẳng. Tam giác $i$ bao tam giác $j$ nếu 3 đỉnh của tam giác $j$ đều nằm trong tam giác $i$ (có thể nằm trên cạnh). Hãy tìm dãy tam giác bao nhau có nhiều tam giác nhất. Điều kiện: $1\le n\le 1000$ và tọa độ các đỉnh của các tam giác thuộc đoạn ${-10}^6$ đến $10^6$.

Hướng dẫn:

Sắp xếp các tam giác tăng dần về diện tích. Khi đó tam giác $i$ sẽ bao tam giác $j$ nếu $j<i$ và 3 đỉnh của $j$ nằm trong $i$. Từ đó có thể đưa về bài toán tìm dãy “tăng” dài nhất.

Bài toán có một số biến thể khác như tìm dãy hình tam giác, hình chữ nhật… bao nhau có tổng diện tích lớn nhất.

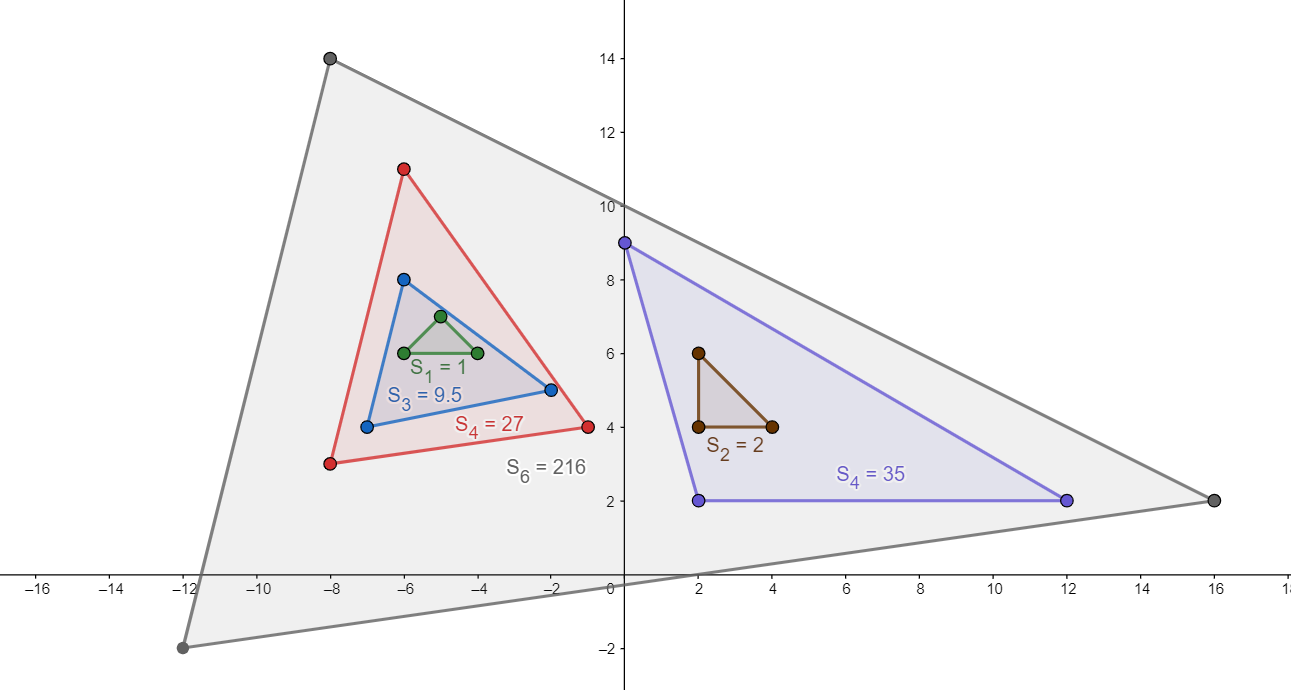
Việc kiểm tra điểm $M$ có nằm trong tam giác $ABC$ không có thể dựa trên 2 phương pháp sau:

  • Tính diện tích: điểm $M$ nằm trong nếu $S(ABC) = S(ABM) + S(ACM) + S(BCM)$.
  • Kẻ một tia song song $Ox$ từ $M$ và đếm số giao điểm với $3$ đoạn $AB,BC,CA$. Nếu số giao điểm là số lẻ thì $M$ nằm trong tam giác.

Dãy đổi dấu

Cho dãy số nguyên gồm $n$ phần tử $a_1, a_2,\ldots, a_n$ và các số nguyên dương $L,U$. Hãy tìm dãy con đổi dấu dài nhất của dãy đó. Dãy con của dãy $a$ là dãy thu được bằng cách xóa đi một số phần tử của $a$. Điều kiện: $1\le L\le n\le1000, 1\le U\le10^9$ và $1\le a_1, a_2,\dots, a_n\le10^9$.

Dãy con đổi dấu $a_{i_1},a_{i_2},\ldots, a_{i_k}$ phải thoả mãn các điều kiện sau:

  • $A_{i_1} < A_{i_2} > A_{i_3} <\ldots$ hoặc $A_{i_1} > A_{i_2} < A_{i_3} >\ldots$
  • Các chỉ số phải cách nhau ít nhất $L: i_2 - i_1 \ge L, i_3 - i_2 \ge L, \ldots$
  • Chênh lệch giữa 2 phần tử liên tiếp không vượt quá $U:$ $|A_{i1} - A_{i2}| \le U,$ $|A_{i2} - A_{i3}| \le U, \ldots$

Hướng dẫn:

Gọi $Q[i]$ là số phần tử của dãy con đổi dấu có phần tử cuối cùng là $a_i$ và phần tử cuối cùng lớn hơn phần tử đứng trước. Tương tự, $P[i]$ là số phần tử của dãy con đổi dấu có phần tử cuối cùng là $a_i$ và phần tử cuối cùng nhỏ hơn phần tử đứng trước.

Ta dễ dàng suy ra:

  • $Q[i] = \max (1, P[j] + 1)$, với mọi $j$ thỏa mãn: $j \le i-L$ và $A_i - U \le A_j < A_i$.
  • $P[i] = \max (1, Q[j] + 1)$, với mọi $j$ thỏa mãn: $j \le i-L$ và $A_i < A_j \le A_i + U$.
#include <iostream>
using namespace std;

const int N = 1e3 + 10;
int a[N], P[N], Q[N], n, U, L;

int main()
{
    cin >> n >> U >> L;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i <= n; i++)
    {
        P[i] = 1; Q[i] = 1;
        for (int j = 1; j <= i - L; j++)
        {
            if (a[i] - U <= a[j] && a[j] < a[i])
                Q[i] = max(Q[i], P[j] + 1);
            if (a[j] > a[i] && a[j] <= a[i] + U)
                P[i] = max(P[i], Q[j] + 1);
        }
    }
    int mx = Q[1];
    for (int i = 1; i <= n; i++)
        mx = max(mx, max(P[i], Q[i]));
    cout << mx;
}

Dãy số WAVIO

Dãy số nguyên $a_1,a_2,a_3,\ldots,a_k$ được gọi là dãy số WAVIO nếu tồn tại số tự nhiên $1\le m\le k$ sao cho:

  • $a_1\le a_2 \le \ldots \le a_m$
  • $a_k\le a_{k-1} \le \ldots \le a_m$

Ví dụ dãy số 1 2 3 4 5 2 1 là 1 dãy WAVIO độ dài 7. Cho dãy $a$ gồm $n$ số nguyên, hãy chỉ ra một dãy con Wavio có độ dài lớn nhất trích ra từ dãy đó. Điều kiện: $1\le n\le 1000$ và $1\le a_1,a_2,\ldots,a_n\le10^9$ với mọi $i=1;2;\ldots;n$.

Hướng dẫn:

Ta sẽ quy hoạch động theo phần tử $a_m$ của dãy WAVIO như sau:

  • $Q[i]$ là độ dài của dãy con tăng dần dài nhất kết thúc ở $i$
  • $P[i]$ là độ dài của dãy con giảm dần dài nhất bắt đầu ở $i$

Khi đó, trong các dãy WAVIO có $i$ là đỉnh thì dãy dài nhất sẽ có độ dài $Q[i]+P[i]-1$. Đến đây, chỉ cần tìm $\max(Q[i]+P[i]-1)$.

Intermediate

Ở mục này, chúng ta sẽ làm quen với QHĐ hai chiều, ta bắt đầu bằng ví dụ sau:

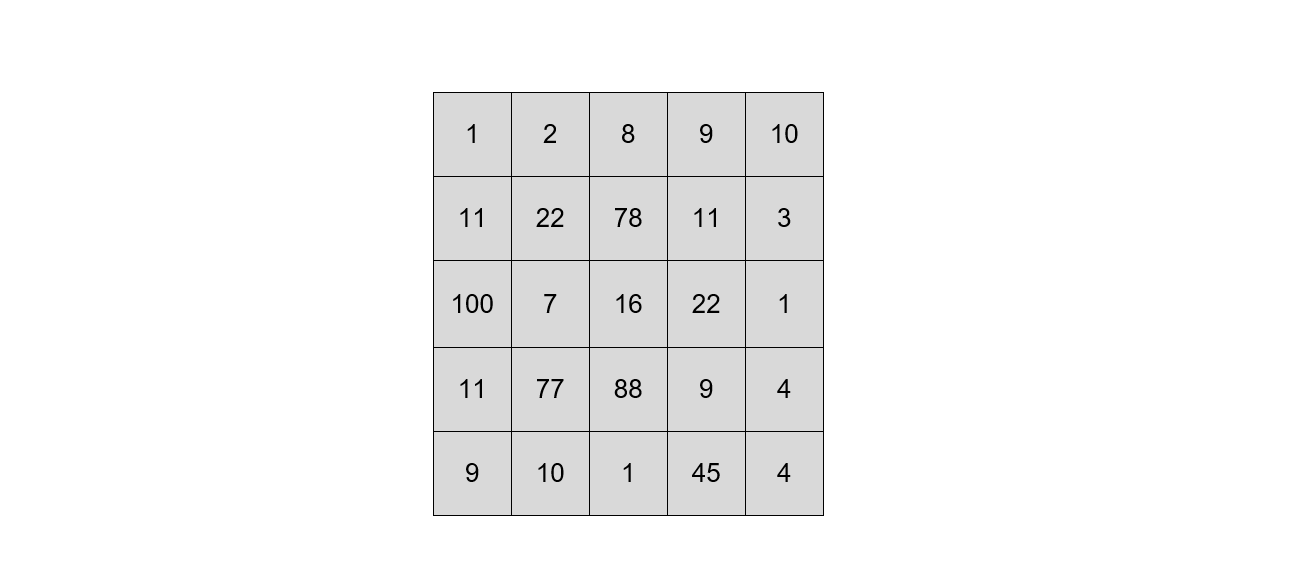
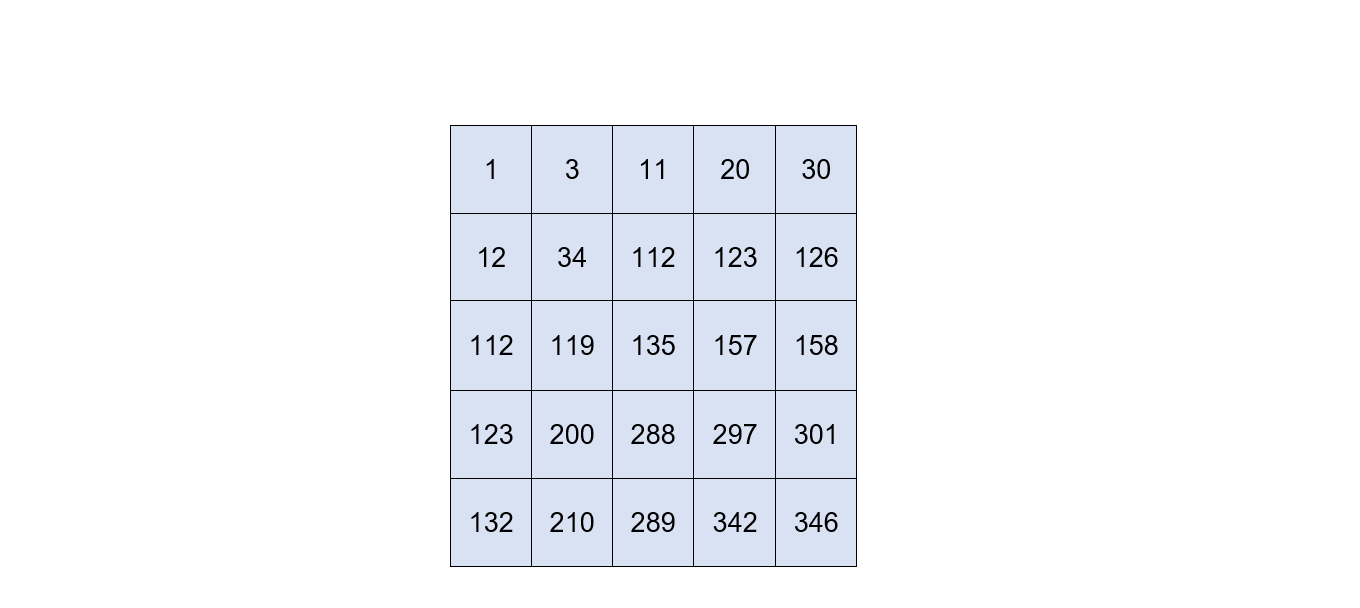
Cho một bảng ô vuông gồm $m$ hàng và $n$ cột. Kí hiệu $(i, j)$ là ô ở hàng $i$, cột $j$. Giả sử $(i, j)$ có $a_{i,j}$ quả táo. Bạn An muốn đi từ $(1, 1)$ đến $(m, n)$. Ở mỗi bước, An đi sang phải hoặc xuống dưới đúng một ô. Khi An ở ô $(i, j)$, An có thể lấy hết các quả táo ở ô đó. Tính số quả táo nhiều nhất mà An có thể lấy được. Điều kiện: $1\le mn\le10^6$ và $1\le a_{i, j}\le 10^9$ với mọi $i,j$.

Ý tưởng:

Bài toán này cũng tương tự như các ví dụ trước.

Đầu tiên, trạng thái của bài toán chính là số quả táo nhiều nhất An có thể lấy khi đi từ ô $(1,1)$ đến ô $(i,j)$, gọi là $f[i][j]$.

Đầu tiên ta khởi tạo $f[1][1] = a_{1,1}$.

Với mọi $i,j\ge 2$, để đi từ $(1, 1)$ đến $(i, j)$ An có hai lựa chọn: đi qua $(i - 1, j)$ hoặc đi qua $(i, j - 1)$. An sẽ chọn đường đi thu được nhiều táo nhất, do đó $f[i][j] = a_{i, j} + \max(f[i][j - 1], f[i - 1][j])$.

#include <iostream>
using namespace std;

const int N = 1e3 + 10;
int m, n, a[N][N];
long long f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            cin >> a[i][j];
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j];
    cout << f[m][n];
}

Ví dụ khác

AvoidRoads - 2003 TCO Semifinals 4 ChessMetrics - 2003 TCCC Round 4

QHĐ hai chiều được áp dụng nhiều trong những bài toán phức tạp hơn. Tiêu biểu là lớp bài toán xếp đồ.

Xếp vali (Knapsack)

Mô hình

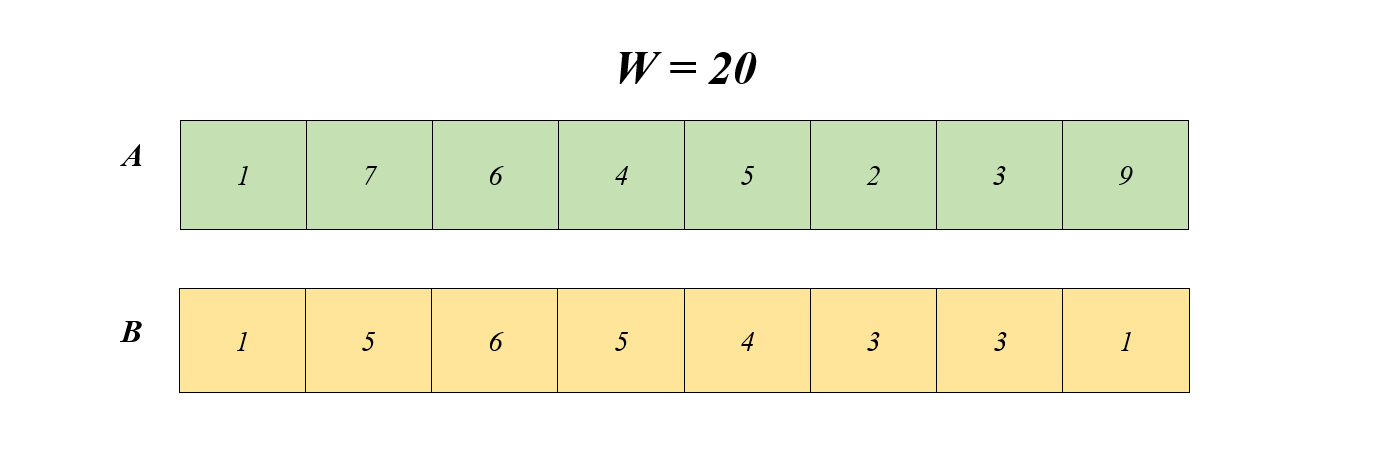
Có $n$ đồ vật, vật thứ $i$ có trọng lượng $A_i$ và giá trị $B_i$. Hãy chọn ra một số các đồ vật, mỗi vật một cái để xếp vào 1 vali có trọng lượng tối đa $W$ sao cho tổng giá trị của vali là lớn nhất.

Công thức

Trạng thái bài toán: tổng giá trị lớn nhất của vali nếu khối lượng không vượt quá $i$.

Nhận xét: giá trị của vali phụ thuộc vào 2 yếu tố: có bao nhiêu vật đang được xét và trọng lượng của các vật. Do đó bảng phương án sẽ là bảng 2 chiều:

  • $L[i,j]$: tổng giá trị lớn nhất của vali khi xét từ vật 1 đến vật $i$ và trọng lượng của vali chưa vượt quá $j$. Chú ý rằng khi xét đến $L[i,j]$ thì các giá trị trên bảng phương án đều đã được tối ưu.

Tính $L[i,j]$: vật đang xét là $A_i$ với trọng lượng của vali không được quá $j$. Có 2 khả năng xảy ra:

  • Nếu chọn $A_i$ đưa vào vali, trọng lượng vali trước đó phải không quá $j - A_i$. Vì mỗi vật chỉ được chọn 1 lần nên giá trị lớn nhất của vali lúc đó là $L[i-1, j - A_i] + B_i$.
  • Nếu không chọn $A_i$, trọng lượng của vali là như cũ (như lúc trước khi chọn $A_i$): $L[i-1,j]$.

Tóm lại ta có $L[i,j] = \max(L[i-1, j - A_i] + B_i, L[i-1, j])$.

2.3. Cài đặt

long long L[1010];

for (int i = 1; i <= n; i++)
    for (int j = 1; j <= W; j++)
        if (A[i] <= j)
            L[i][j] = max(L[i - 1][j - A[i]]  + B[i], L[i - 1][j]);
        else
            L[i][j] = L[i - 1][j];

2.4. Một số bài toán khác

Dãy con có tổng bằng S

Cho dãy $A_1,A_2,\ldots, A_N$. Tìm một dãy con của dãy đó có tổng bằng $S$. Điều kiện: $1\le n\le 1000$ và $1\le A_1,A_2,\ldots,A_n\le10^9$.

Hướng dẫn:

Đặt $L[i,t]=1$ nếu có thể tạo ra tổng $t$ từ một dãy con của dãy gồm các phần tử $A_1,A_2,\ldots,A_i$. Ngược lại thì $L[i,t]=0$. Nếu $L[n,S]=1$ thì đáp án của bài toán trên là “có”.

Ta có thể tính $L[i,t]$ theo công thức: $L[i,t]=1$ nếu $L[i-1,t]=1$ hoặc $L[i-1,t-a[i]]=1$.

Cài đặt:

Nếu áp dụng luôn công thức trên thì ta cần dùng bảng phương án hai chiều. Ta có thể nhận xét rằng để tính dòng thứ $i$, ta chỉ cần dòng $i-1$. Bảng phương án khi đó chỉ cần 1 mảng 1 chiều $L[0..S]$ và được tính như sau:

long long L[1010];

L[0] = 1;
for (int i = 1; i <= n; i++)
    for (int t = S; t >= a[i]; t--)
        if (L[t - a[i]] == 1)
            L[t] = 1;

Dễ thấy độ phức tạp bộ nhớ của cách cài đặt trên là $O(m)$, độ phức tạp thời gian là $O(nm)$, với $m$ là tổng của $n$ số.

Bonus: Hãy thử kiểm tra xem vì sao trong vòng for thứ hai, $t$ được duyệt từ $S$ về $a[i]$ chứ không phải từ $a[i]$ lên $S$.

Chia kẹo

Cho $n$ gói kẹo, gói thứ $i$ có $a_i$ viên. Hãy chia các gói thành 2 phần sao cho chênh lệch giữa 2 phần là ít nhất. Điều kiện: $1\le n\le 300$ và $1\le a_1,a_2,\ldots,a_n\le1000$.

Hướng dẫn:

Gọi $T$ là tổng số kẹo của $n$ gói. Chúng ta cần tìm số $S$ lớn nhất thoả mãn:

  • $S \le T/2$.
  • Có một dãy con của dãy $a$ có tổng bằng $S$.

Khi đó sẽ có cách chia với chênh lệch 2 phần là $T-2S$ là nhỏ nhất và dãy con có tổng bằng $S$ ở trên gồm các phần tử là các gói kẹo thuộc phần thứ nhất. Phần thứ hai là các gói kẹo còn lại. Ta quy hoạch động mảng $L[i,j]$ $(j\le \frac{T}{2})$ như sau: $L[i,j]=true$ nếu tồn tại một số phần tử của dãy $a$ từ $1$ đến $i$ có tổng bằng $j$. Khi đó:

  • Nếu $L[i-1,j]=true$ thì $L[i,j] = true$.
  • Nếu $L[i-1,j-a[i]]=true$ thì $L[i,j] = true$.

Cuối cùng, ta cần tìm số $j$ lớn nhất không vượt quá $\frac{T}{2}$ sao cho tồn tại số nguyên dương $i$ để $L[i,j]=true$, hay $L[n,j]=true$. 

#include <iostream>
using namespace std;

const int N = 310;
int n, a[N];
bool L[N][N];

int main()
{
    cin >> n;
    int t = 0;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        t += a[i];
    }
    for (int i = 0; i <= n; i++)
        L[i][0] = true;
    for (int i = 1; i <= n; i++)
        for (int j = 1; 2 * j <= t; j++)
        {
            L[i][j] |= L[i - 1][j];
            if (a[i] <= j)
                L[i][j] |= L[i - 1][j - a[i]];
        }
    int mx = 0;
    for (int i = 1; 2 * i <= t; i++)
        if (L[n][i])
            mx = i;
    cout << mx << ' ' << t - mx;
}

Market (Olympic Balkan 2000)

Người đánh cá Clement bắt được $n$ con cá, khối lượng con cá thứ $i$ là $a_i$, đem bán ngoài chợ. Ở chợ cá, người ta không mua cá theo từng con mà mua theo một lượng nào đó. Chẳng hạn $3 kg$, $5kg$…

Ví dụ:** có 3 con cá, khối lượng lần lượt là: $3, 2, 4$. Mua lượng $6kg$ sẽ phải lấy con cá thứ 2 và và thứ 3. Mua lượng $3 kg$ thì lấy con thứ nhất. Không thể mua lượng $8 kg$. Nếu bạn là người đầu tiên mua cá, có bao nhiêu lượng bạn có thể chọn? **Điều kiện: $1\le n\le1000$, $1\le a_i\le1000$.

Hướng dẫn

Thực chất bài toán là tìm các số $S$ mà có một dãy con của dãy $a$ có tổng bằng $S$.

Ta có thể dùng phương pháp đánh dấu của bài chia kẹo ở trên rồi đếm các giá trị $t$ mà $L[n, t]=true$.

Điền dấu

Cho $n$ số tự nhiên $A_1,A_2, \ldots,A_n$. Ban đầu các số được đặt liên tiếp theo đúng thứ tự cách nhau bởi dấu "?": A1 ? A2 ? ... ? AN. Cho trước số nguyên $S$, có cách nào thay các dấu ? bằng dấu + hay dấu − để được một biểu thức số học cho giá trị là $S$ không?

Hướng dẫn:

Đặt $L[i,t]=1$ nếu có thể điền dấu vào $i$ số đầu tiên và cho kết quả bằng $t$. Ta có công thức sau để tính $L$:

  • L[1, a[1]] = 1
  • L[i, t] = 1 nếu L[i - 1, t + a[i]] = 1 hoặc L[i - 1, t - a[i]] = 1.

Nếu L[n, S] = 1 thì câu trả lời của bài toán là có.

Khi cài đặt, có thể dùng một mảng 2 chiều (lưu toàn bộ bảng phương án) hoặc 2 mảng một chiều (để lưu dòng $i$ và dòng $i-1$). Chú ý là chỉ số theo $t$ của các mảng phải có cả phần âm (tức là từ $-T$ đến $T$, với $T$ là tổng của $n$ số), vì trong bài này chúng ta dùng cả dấu - nên có thể tạo ra các tổng âm.

Bài này có một biến thể là đặt dấu sao cho kết quả là một số chia hết cho $k$. Ta có thuật giải tương tự bài toán trên bằng cách thay các phép cộng, trừ bằng các phép cộng và trừ theo modulo $k$ và dùng mảng đánh dấu với các giá trị từ 0 đến $k-1$ (là các số dư có thể có khi chia cho $k$). Đáp số của bài toán là $L[n,0]$.

Expression

Cho $n$ số nguyên dương. Hãy chia chúng thành 2 nhóm sao cho tích của tổng 2 nhóm là lớn nhất.

Hướng dẫn:

  • Gọi $T$ là tổng $n$ số nguyên đó. Giả sử ta chia dãy thành 2 nhóm, gọi $S$ là tổng của một nhóm, tổng nhóm còn lại là $T-S$ và tích của tổng 2 nhóm là $S(T-S)$. Bằng phương pháp đánh dấu ta xác định được mọi số $S$ là tổng của một nhóm (như bài Market) và tìm số $S$ sao cho $S(T-S)$ đạt $\max$.
  • Bài toán trên có thể đưa về bài chia kẹo. Không mất tính tổng quát, giả sử $S\le \frac{T}{2}$. Để ý rằng $S+(T-S)=T$, là một số cố định. Có thể chứng minh $S(T-S)$ đạt max khi và chỉ khi $S$ lớn nhất có thể. Khi đó chỉ cần chia các số thành hai nhóm sao cho chênh lệch giữa hai nhóm là ít nhất.

Farmer (IOI 2004)

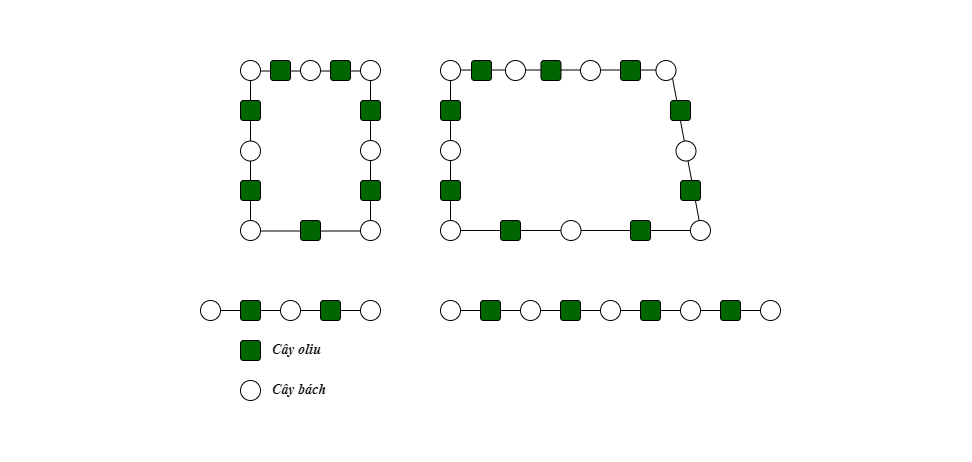
Một người có $N$ mảnh đất và $M$ dải đất. Các mảnh đất có thể coi là một tứ giác và các dải đất thì coi như một đường thẳng. Dọc theo các dải đất ông ta trồng các cây bách, dải đất thứ $i$ có $A_i$ cây bách. Ông ta cũng trồng các cây bách trên viền của các mảnh đất, mảnh đất thứ $j$ có $B_j$ cây bách. Cả ở trên các mảnh đất và dải đất, xen giữa 2 cây bách ông ta trồng một cây ôliu. Ông ta cho con trai được chọn các mảnh đất và dải đất tuỳ ý với điều kiện tổng số cây bách không vượt quá $Q$. Người con trai phải chọn thế nào để có nhiều cây ôliu (loài cây mà anh ta thích) nhất.

Hướng dẫn

Dễ thấy mảnh đất thứ $i$ có $A_i$ cây ôliu và dải đất thứ $j$ có $B_j-1$ cây ôliu. Coi các mảnh đất và dải đất là các “đồ vật”, đồ vật thứ $k$ có khối lượng $W_k$ và giá trị $V_k$ (nếu $k$ là mảnh đất $i$ thì $W_k=V_k=A_i$, nếu $k$ là dải đất $j$ thì $W_k=B_j,V_k=B_j-1$). Ta cần chọn các “đồ vật”, sao cho tổng “khối lượng” của chúng không vượt $Q$ và tổng “giá trị” là lớn nhất. Đây chính là bài toán xếp balô đã trình bày ở trên.

Kết

Quy hoạch động là phương pháp tự nhiên và có thể áp dụng được trong rất nhiều bài toán. Khi gặp một bài toán, hãy để ý xem nó có được giải trong thời gian đa thức không. Nếu có, hãy thử xác định trạng thái của nó và mối liên hệ giữa các trạng thái. Đôi khi ta cần phân tích một chút để đưa bài toán về QHĐ như các ví dụ ở trên.

Chúc các bạn học tập tốt!