Trie
Nguời viết:
- Ngô Nhật Quang - HUS High School for Gifted Students
Reviewer:
- Hồ Ngọc Vĩnh Phát - VNUHCM-University of Science
- Lê Minh Hoàng - VNUHCM-University of Science
- Cao Thanh Hậu - VNUHCM-University of Science
Giới thiệu
Trie, hay một số tài liệu còn gọi là cây tiền tố, là một cấu trúc dữ liệu dạng cây hữu dụng được dùng để quản lí một tập hợp các xâu. Mặc dù dễ hiểu và dễ cài đặt, trie lại có rất nhiều ứng dụng. Do vậy, trie thường xuyên xuất hiện trong các cuộc thi lập trình ở Việt Nam nói riêng và quốc tế nói chung.
Một trie cơ bản có thể thực hiện ba thao tác sau với độ phức tạp thời gian tuyến tính:
- Thêm một xâu vào tập hợp
- Xóa một xâu khỏi tập hợp
- Kiểm tra một xâu có nằm trong tập hợp đó hay không
Cấu trúc
Trie là một cấu trúc dữ liệu dạng cây dùng để lưu trữ một danh sách các xâu với bộ kí tự hữu hạn, cho phép việc lưu trữ các xâu hiệu quả có tiền tố giống nhau.
Hãy xem xét một ví dụ sau:
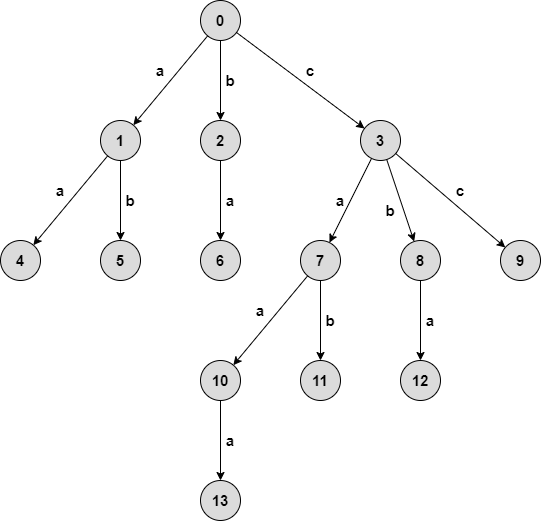
Trong một trie, mỗi cạnh được biểu diễn bằng một kí tự, mỗi đỉnh và đường đi từ gốc đến đỉnh đó biểu diễn một xâu gồm các kí tự thuộc các cạnh trên đường đi đó. Ví dụ, đỉnh $5$ biểu diễn xâu ab, đỉnh $10$ biểu diễn xâu caa.
Cấu trúc của trie rất dễ hiểu và cài đặt. Gọi child(u, c) là đỉnh con của đỉnh $u$ được nối bởi cạnh được biểu diễn bằng kí tự $c$, hoặc bằng $-1$ nếu đỉnh con đó không tồn tại. Xâu được thể hiện bởi đỉnh con này sẽ chính là xâu được thể hiện bởi đỉnh $u$, thêm kí tự $c$ vào cuối. Do vậy, ta chỉ cần mảng child này với mỗi đỉnh để duy trì cấu trúc của trie. Ví dụ, trong ảnh trên, child(1, 'b') = 5, child(3, 'c') = 9, child(11, 'b') = -1.
Cài đặt
Với cấu trúc dữ liệu trie, có hai cách cài đặt chính chính là sử dụng mảng và sử dụng con trỏ.
Nếu định nghĩa cấu trúc như phần trước, ta chỉ có thể thực hiện truy vấn thêm xâu vào tập hợp. Để thực hiện hai truy vấn còn lại, với mỗi đỉnh $u$ trong trie, ta lưu thêm hai biến:
-
exist: có bao nhiêu xâu là xâu được thể hiện bởi đỉnh $u$ -
cnt: có bao nhiêu xâu có tiền tố là xâu được thể hiện bởi đỉnh $u$.
Lưu ý: Tuy nhiên với từng bài toán, hai biến này có thể không cần thiết và có thể bỏ đi.
Với hàm thêm xâu vào trie, ta bắt đầu tại nút gốc. Ta duyệt qua lần lượt các kí tự trong xâu và đi xuống cạnh chứa kí tự tương ứng. Nếu như cạnh tương ứng đó chưa tồn tại thì ta tạo đỉnh mới rồi thêm nó vào mảng child. Dưới đây là ví dụ trie của tập hợp các xâu aa, aba, ba, caaa, cab, cba, ca.

Ở hàm xóa xâu, đầu tiên kiểm tra xâu đó có tồn tại trong trie hay không. Nếu có nhiều xâu như vậy, ta giảm giá trị exist của đỉnh tương ứng xâu đó đi một. Nếu không, ta sẽ đệ quy từ dưới lên trên để xóa dần các đỉnh dư thừa.
Hàm tìm xâu được cài đặt khá giống hàm thêm xâu. Chỉ khác là nếu không có cạnh tương ứng với kí tự đang duyệt, ta dừng ngay lập tức vì xâu đó sẽ không thể xuất hiện trong trie. Sau khi duyệt xong ta kiểm tra ở đỉnh đó có xâu nào kết thúc hay không, hay exist != 0.
Cài đặt bằng mảng
const int NUMBEROFNODES = ...;
struct Trie{
struct Node{
int child[26];
int exist, cnt;
} nodes[NUMBEROFNODES];
int cur; // Hiện trong trie đang có bao nhiêu đỉnh
Trie() : cur(0) { // Tạo nút gốc cho Trie là đỉnh 0 khi khởi tạo Trie
memset(nodes[0].child, -1, sizeof(nodes[cur].child));
nodes[0].exist = nodes[0].cnt = 0;
};
int new_node() { // Tạo và trả về giá trị của đỉnh mới được tạo ra
cur++;
memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
nodes[cur].exist = nodes[cur].cnt = 0;
return cur;
}
void add_string(string s) {
int pos = 0;
for (auto f : s) {
int c = f - 'a';
if (nodes[pos].child[c] == -1) { // Nếu cạnh tương ứng chữ cái c
// chưa tồn tại thì ta tạo ra đỉnh mới
nodes[pos].child[c] = new_node();
}
pos = nodes[pos].child[c];
nodes[pos].cnt++; // Có thêm một xâu trong trie có tiền tố
// là xâu được thể hiện bằng đỉnh hiện tại
}
nodes[pos].exist++; // Đã tìm được đỉnh tương ứng với xâu s,
// ta tăng biến exist của đỉnh lên 1
}
bool delete_string_recursive(int pos, string& s, int i) { // Trả về liệu đỉnh pos
// có bị xóa đi hay không
if (i != (int)s.size()) { // Nếu chưa đến đỉnh tương ứng với xâu s
// thì tiếp tục đệ quy xuống dưới
int c = s[i] - 'a';
bool isChildDeleted = delete_string_recursive(nodes[pos].child[c], s, i + 1);
if (isChildDeleted) nodes[pos].child[c] = -1; // Nếu đỉnh con tương ứng bị xóa thì
// ta gán lại đỉnh tương ứng bằng -1
}
else nodes[pos].exist--; // Nếu đã đến đỉnh tương ứng với xâu s
// thì ta giảm biến exist của đỉnh đi 1
if (pos != 0) { // Nếu đỉnh đang xét không phải gốc thì ta giảm biến cnt của đỉnh đi 1
// và kiểm tra đỉnh có bị xóa đi hay không
// Đỉnh bị xóa nếu không còn xâu nào đi qua nó, nói cách khác là
// không còn xâu nào có tiền tố là xâu được thể hiện bởi đỉnh pos
nodes[pos].cnt--;
if (nodes[pos].cnt == 0) return true;
}
return false;
}
void delete_string(string s) {
if (find_string(s) == false) return; // Kiểm tra xâu s có trong
// trie hay không
delete_string_recursive(0, s, 0); // Gọi hàm đệ quy xóa xâu s khỏi trie
}
bool find_string(string s) {
int pos = 0;
for (auto f : s) {
int c = f - 'a';
if (nodes[pos].child[c] == -1) return false;
pos = nodes[pos].child[c];
}
return (nodes[pos].exist != 0); // Kiểm tra có xâu nào
// kết thúc tại đỉnh này hay không
}
};Cài đặt bằng con trỏ
Gần như mọi phần trong đoạn code dưới hoạt động giống phần cài đặt bằng mảng nên sẽ không chú thích lại.
struct Trie{
struct Node{
Node* child[26];
int exist, cnt;
Node() {
for (int i = 0; i < 26; i++) child[i] = NULL;
exist = cnt = 0;
}
};
int cur;
Node* root;
Trie() : cur(0) {
root = new Node();
};
void add_string(string s) {
Node* p = root;
for (auto f : s) {
int c = f - 'a';
if (p->child[c] == NULL) p->child[c] = new Node();
p = p->child[c];
p->cnt++;
}
p->exist++;
}
bool delete_string_recursive(Node* p, string& s, int i) {
if (i != (int)s.size()) {
int c = s[i] - 'a';
bool isChildDeleted = delete_string_recursive(p->child[c], s, i + 1);
if (isChildDeleted) p->child[c] = NULL;
}
else p->exist--;
if (p != root) {
p->cnt--;
if (p->cnt == 0) {
delete(p); // Khác với cài đặt bằng mảng,
// ta có thể thực sự xóa đỉnh này đi
return true;
}
}
return false;
}
void delete_string(string s) {
if (find_string(s) == false) return;
delete_string_recursive(root, s, 0);
}
bool find_string(string s) {
Node* p = root;
for (auto f : s) {
int c = f - 'a';
if (p->child[c] == NULL) return false;
p = p->child[c];
}
return (p->exist != 0);
}
};Ưu và nhược điểm của cài đặt bằng con trỏ
Ưu điểm:
- Không cần phải tính toán trước độ dài mảng cần dùng. Tuy có thể cài đặt trie bằng vector nhưng sẽ tốn thời gian truy cập hơn và đôi khi tốn nhiều bộ nhớ hơn.
- Có thể tạo nhiều trie mà không lo tới bộ nhớ, phù hợp với các bài multitest.
- Có thể xóa thực sự các đỉnh dư thừa.
Nhược điểm:
- Dễ code sai nếu không thực sự hiểu con trỏ là gì.
- Tùy thuộc vào compiler mà con trỏ có thể còn tốn nhiều bộ nhớ hơn dùng mảng.
Trong phần còn lại của bài viết, tác giả sẽ ưu tiên cài đặt trie bằng mảng nếu được. Bạn đọc lưu ý xem tùy vào bài toán mà lựa chọn cách cài đặt phù hợp.
Trie nhị phân
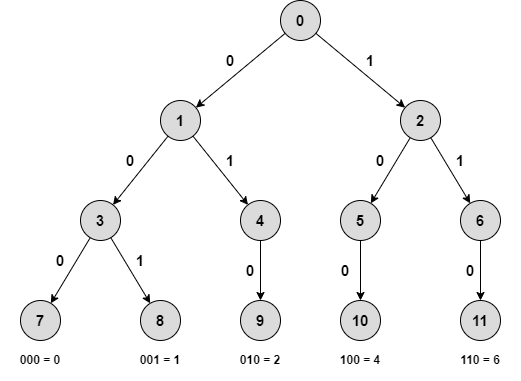
Có cấu trúc tương tự với trie đã giới thiệu ở phần trước (tạm gọi là trie xâu), trie nhị phân được dùng để xử lí một số bài toán liên quan tới thao tác bit. Một trie nhị phân bao gồm các cạnh là bit $0/1$ và các đỉnh là các số nguyên gồm các bit trên đường đi từ gốc đến nó.
Các số được thêm vào trie sẽ được chuyển thành dạng nhị phân rồi thêm các bit $0$ vào đầu sao cho độ dài các số nhị phân đều bằng nhau. Thông thường độ dài này sẽ được đặt là ${\log_2{(\max a_i)}}$ với $a_i$ là các số trong danh sách đã cho. Khi thêm vào trie, ta sẽ thêm các bit vào trie theo chiều từ trái sang phải.
Lưu ý rằng các ứng dụng của trie xâu (liệt kê bên dưới) đều có thể được áp dụng cho trie nhị phân.
const int NUMBEROFNODES = ...;
const int LG = ...;
struct Trie{
struct Node{
int child[2];
int exist, cnt;
} nodes[NUMBEROFNODES];
int cur;
Trie() : cur(0) {
memset(nodes[0].child, -1, sizeof(nodes[cur].child));
nodes[0].exist = nodes[0].cnt = 0;
};
int new_node() {
cur++;
memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
nodes[cur].exist = nodes[cur].cnt = 0;
return cur;
}
void add_number(int x) {
int pos = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (nodes[pos].child[c] == -1) nodes[pos].child[c] = new_node();
pos = nodes[pos].child[c];
nodes[pos].cnt++;
}
nodes[pos].exist++;
}
void delete_number(int x) {
if (find_number(x) == false) return;
int pos = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
int tmp = nodes[pos].child[c];
nodes[tmp].cnt--;
if (nodes[tmp].cnt == 0) {
nodes[pos].child[c] = -1;
return;
}
pos = tmp;
}
nodes[pos].exist--;
}
bool find_number(int x) {
int pos = 0;
for (int i = LG; i >= 0; i--) {
int c = (x & (1 << i) ? 1 : 0);
if (nodes[pos].child[c] == -1) return false;
pos = nodes[pos].child[c];
}
return (nodes[pos].exist != 0);
}
};Ứng dụng
Trie tuy trông đơn giản nhưng nó có rất nhiều ứng dụng khác nhau, xử lí các thao tác trên các danh sách số nguyên và danh sách xâu.
Trong đời sống, trie là nền tảng cho một số thứ chúng ta rất thân thuộc như các công cụ tìm kiếm(Google, Bing, …), tính năng tự động hoàn thành từ (autocomplete), … nhưng trong bài viết này sẽ tập trung vào các ứng dụng trong lập trình thi đấu.
Sắp xếp một danh sách các xâu
Bài toán
Cho một danh sách các xâu, hãy in ra các xâu đó theo thứ tự từ điển tăng dần.
Lời giải
Sau khi xây dựng trie gồm các xâu trong danh sách, ta dfs một lượt qua trie đó, đi lần lượt các cạnh theo thứ tự chữ cái tăng dần. Duyệt tới một đỉnh tới bất kì, ta sẽ in ra các xâu được thể hiện bởi đỉnh đó nếu có. Dễ thấy ta sẽ lần lượt thu được các xâu trong danh sách theo thứ tự từ điển tăng dần.
Qua đó mà ta đạt được thuật toán sắp xếp một danh sách các xâu trong thời gian tuyến tính.

void dfs(int pos, string& current_string, vector<string>& res) {
for (int i = 1; i <= nodes[pos].exist; i++) res.push_back(current_string);
for (int i = 0; i < 26; i++) if (nodes[pos].child[i] != -1) {
current_string += char(i + 'a');
dfs(nodes[pos].child[i], current_string, res);
current_string.pop_back();
}
}
vector<string> sort_strings() {
vector<string> res;
string current_string = "";
dfs(0, current_string, res);
return res;
}Xử lí truy vấn tiền tố chung dài nhất của hai xâu
Bài toán
Cho một danh sách các xâu. Hãy trả lời các truy vấn tìm độ dài của tiền tố chung dài nhất của hai xâu bất kì trong danh sách đó.
Lời giải
Đầu tiên, ta dựng một trie của danh sách các xâu đã cho.
Với hai xâu bất kì trong danh sách, ta có thể thấy tiền tố chung dài nhất của chúng cũng có thể được thể hiện bằng một đỉnh trong trie. Nhìn hình vẽ ta có dễ dàng nhận ra đỉnh cần tìm này cũng chính là tổ tiên chung thấp nhất của hai đỉnh thể hiện cho hai xâu đã cho.
Do vậy bài toán quy về xử lí truy vấn tìm tổ tiên chung thấp nhất của hai đỉnh bất kì trên cây, bạn đọc có thể tham khảo lời giải ở blog này.
Xử lí truy vấn tìm xâu có thứ tự từ điển thứ k
Bài toán
Cho một danh sách các xâu. Xử lí các truy vấn tìm xâu có thứ tự từ điển lớn thứ $k$.
Lời giải
Tương tự như bài toán trước, ta xây dựng một trie cho các xâu trong danh sách đã cho.
Ta tham khảo hàm tìm đáp án dưới đây:
string find_kth_string(int k) {
int pos = 0;
string res = "";
while (true) {
if (nodes[pos].exist >= k) break;
k -= nodes[pos].exist;
for (int i = 0; i < 26; i++) if (nodes[pos].child[i] != -1) {
int nxt = nodes[pos].child[i];
if (nodes[nxt].cnt >= k) {
res += char(i + 'a');
pos = nxt;
break;
}
k -= nodes[nxt].cnt;
}
}
return res;
}Trong đoạn code, dễ thấy rằng ta xây dựng đáp án từ trái qua phải. Ở đỉnh hiện tại đang xét, ta sử dụng biến đếm $cnt$ ở mỗi đỉnh con để xác định kí tự tiếp theo của xâu đáp án là gì. Sau đó di chuyển xuống đỉnh con đó để tiếp tục tìm kí tự tiếp theo.
Xử lí truy vấn tìm XOR lớn nhất với giá trị được cho
Đây là một bài toán điển hình sử dụng trie nhị phân. Đa số các bài toán liên quan tới thao tác bit sử dụng trie đều là biến thể của bài toán này.
Bài toán
Cho danh sách các số nguyên không âm $a_1, a_2, \ldots, a_n$. Xử lí các truy vấn cho số nguyên không âm $x$, tìm $\max_{i = 1}^{n} a_i \oplus x$ với $\oplus$ là phép XOR hai số nguyên không âm.
Lời giải
Đầu tiên xây dựng một trie nhị phân với các số nguyên đã cho.
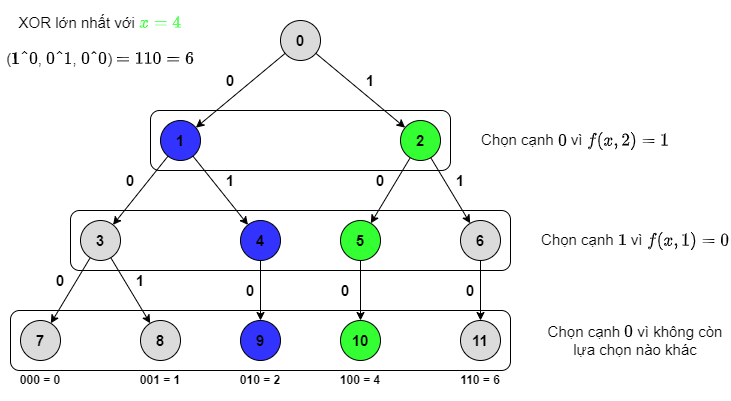
Xét lần lượt các bit từ lớn đến bé của đáp án. Coi bit đang xét là bit thứ $i$. Ta sẽ xây dựng đáp án một cách tham lam bằng cách cố gắng đặt bit thứ $i$ của đáp án là $1$ do $2^i > \sum_{i = 0}^{j - 1}2^j$. Nói cách khác, dù đặt cả $i - 1$ bit còn lại của đáp án là $1$ thì cũng không có lợi bằng đặt bit $i$ là $1$.
Ta sẽ lần lượt xây đáp án bằng các đi xuống từ gốc của trie. Coi ta đang xây bit thứ $i$ của đáp án. Nếu đỉnh hiện tại đang xét có thể đi xuống cạnh có bit là $f(x, i) \oplus 1$ với $f(x, i)$ là bit thứ $i$ của số $x$, ta sẽ đi qua cạnh đó để có được bit $i$ trong đáp án là $1$. Nếu không, ta "đành" đi xuống cạnh còn lại của đỉnh đang xét và có được bit $i$ của đáp án là $0$.
int query(int x) {
int pos = 0, res = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (nodes[pos].child[c ^ 1] != -1) {
res += (1ll << i);
pos = nodes[pos].child[c ^ 1];
}
else {
pos = nodes[pos].child[c];
}
}
return res;
}Áp dụng
Dưới đây sẽ là một số bài toán hay (theo góc nhìn của người viết) và lời giải dễ hiểu sử dụng cấu trúc dữ liệu trie.
Codeforces - Kuro and GCD and XOR and SUM
Đề bài
Cho mảng số $a$ ban đầu rỗng. Xử lí $q$ truy vấn thuộc hai loại sau:
- $1\,u_i$: Thêm số $u_i$ vào mảng $a$.
- $2\,x_i\,k_i\,s_i$: Tìm số $v$ thuộc mảng $a$ sao cho $GCD(x_i, v)$ chia hết cho $k_i$, $x_i + v \le s_i$, và $x_i \oplus v$ là lớn nhất có thể với $GCD(a, b)$ là ước chung lớn nhất của $a$ và $b$. In ra $-1$ nếu không có số $v$ nào trong mảng $a$ thỏa mãn.
Giới hạn:
- $2 \le q \le 10^5$
- $1 \le u_i, x_i, k_i, s_i \le 10^5$
Lời giải
Nhìn thấy bài toán tìm $x_i \oplus v$ lớn nhất ngay lập tức gợi cho chúng ta lời giải sử dụng trie để giải. Vì vậy ta sẽ cố gắng thiết kế trie để truy vấn trên tập các số thỏa mãn hai điều kiện còn lại.
Để $GCD(x_i, v)$ chia hết cho $k_i$, dễ nhận thấy cả $x_i$ và $v$ đều phải chia hết cho $k_i$. Do vậy, ta sẽ tạo $10^5$ trie, với trie thứ $i$ là các số trong mảng $a$ chia hết cho $i$. Để $x_i + v \le s_i$ thì dĩ nhiên $v \le s_i - x_i$, ta lưu với mỗi đỉnh trong trie số bé nhất trong cây con của đỉnh đó là bao nhiêu.
Vậy để giải quyết một truy vấn, ta sẽ tìm giá trị XOR lớn nhất trên trie thứ $k_i$ (cách giải đã trình bày ở trên) và chỉ đi vào một đỉnh con nếu như giá trị bé nhất của cây con đó bé hơn hoặc bằng $s_i - x_i$.
Code mẫu
#include <bits/stdc++.h>
using namespace std;
const int LG = 18;
const int INF = 1e9;
struct Trie{
struct Node{
Node* child[2];
int mn;
Node() {
for (int i = 0; i < 2; i++) child[i] = NULL;
mn = INF;
}
};
int cur;
Node* root;
Trie() : cur(0) {
root = new Node();
};
void add_number(int x) {
Node* p = root;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (p->child[c] == NULL) p->child[c] = new Node();
p = p->child[c];
p->mn = min(p->mn, x);
}
}
int query(int x, int val) {
Node* p = root;
int res = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (p->child[c ^ 1] != NULL && p->child[c ^ 1]->mn <= val) {
res += ((c ^ 1) << i);
p = p->child[c ^ 1];
}
else {
if (p->child[c] == NULL || p->child[c]->mn > val) return -1;
p = p->child[c];
res += (c << i);
}
}
return res;
}
};
const int N = 1e5;
Trie tries[N + 5];
vector<int> d[N + 5];
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
for (int i = 1; i <= N; i++) {
for (int j = i; j <= N; j += i) d[j].push_back(i);
}
int q;
cin >> q;
while (q--) {
int t;
cin >> t;
if (t == 1) {
int u;
cin >> u;
for (auto x : d[u]) tries[x].add_number(u);
}
else {
int x, k, s;
cin >> x >> k >> s;
if (x % k != 0) cout << "-1\n";
else cout << tries[k].query(x, s - x) << "\n";
}
}
}Codeforces - Vitya and Strange Lesson
Đề bài
Cho dãy số nguyên không âm $a_1, a_2, \ldots, a_n$ và $m$ truy vấn thuộc hai loại:
- Cho $x$, XOR tất cả các số trong dãy với $x$.
- In ra MEX (số nguyên không âm nhỏ nhất mà không xuất hiện) của dãy.
Giới hạn:
- $1 \le n, m \le 3 \times 10^5$
- $0 \le a_i, x \le 3 \times 10^5$
Lời giải
Với các truy vấn loại $1$, thay vì thay đổi cả dãy, ta nhận thấy rằng $(a \oplus b) \oplus c = a \oplus (b \oplus c)$. Tức là nếu áp dụng hai truy vấn loại $1$ với hai số nguyên $b, c$ thì cũng tương tự như áp dụng một truy vấn với số nguyên $b \oplus c$. Do vậy, ta chỉ cần duy trì cả dãy đang bị XOR bởi số nguyên nào. Gọi số đó là $z$.
Giả dụ ta đã có một trie nhị phân của dãy số $a_1, a_2, \ldots, a_n$ và ta muốn tìm MEX của các số trong đó. Ta sẽ sử dụng thuật toán tương tự chặt nhị phân. Gọi độ cao của trie là $k$. Khởi đầu tại gốc trie, ta kiểm tra xem cây con bên trái (cạnh thể hiện bit $0$) có phải là cây nhị phân hoàn hảo hay không. Nói cách khác, tất cả các số trong khoảng $[0, 2^k - 1]$ có tồn tại hay không. Nếu có, ta chắc chắn MEX của dãy số nằm trong khoảng này. Nếu không, ta chắc chắn MEX của dãy số nằm trong khoảng $[2^k, 2^{k + 1} - 1]$. Sau đó, ta đi xuống đỉnh con tương ứng và tiếp tục xét hai đỉnh con của nó. Làm như vậy với tất cả các bit là sẽ tìm được đáp án.
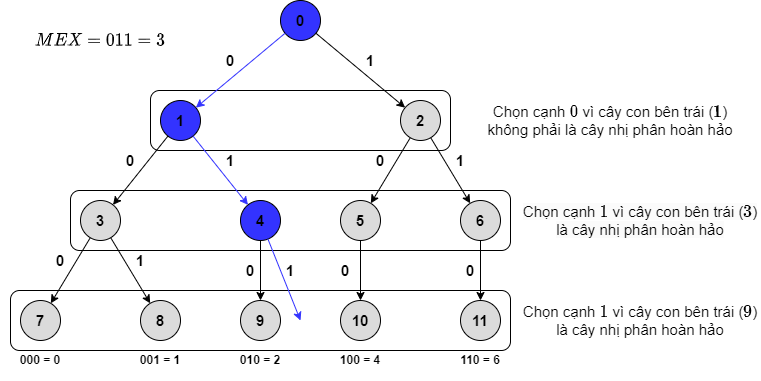
Vậy phần còn lại phải xử lí là kết hợp thuật tìm MEX trên với việc cả mảng đang bị XOR bởi số $z$. Dễ nhận thấy là, nếu bit thứ $k$ của $z$ được bật, thì nó tương tự việc hai cây con trái và phải của đỉnh đang xét được đổi chỗ cho nhau. Vì vậy thuật toán cuối cùng tương tự với thuật toán tìm MEX trên, thêm việc xét bit thứ $k$ của $z$ mà ta sẽ xét cây con trái trước (nếu bit đó là $0$) hay cây con phải trước (nếu bit đó là $1$).
Code mẫu
#include <bits/stdc++.h>
using namespace std;
const int NUMBEROFNODES = 5400005;
const int LG = 18;
struct Trie{
struct Node{
int child[2];
int cnt;
} nodes[NUMBEROFNODES];
int cur;
Trie() : cur(0) {
memset(nodes[0].child, -1, sizeof(nodes[cur].child));
nodes[0].cnt = 0;
};
int new_node() {
cur++;
memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
nodes[cur].cnt = 0;
return cur;
}
void add_number(int x) {
int pos = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (nodes[pos].child[c] == -1) nodes[pos].child[c] = new_node();
pos = nodes[pos].child[c];
nodes[pos].cnt++;
}
}
int query(int x) {
int pos = 0, res = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (nodes[pos].child[c] != -1 && nodes[nodes[pos].child[c]].cnt == (1 << i)) {
pos = nodes[pos].child[c ^ 1];
res += (1 << i);
}
else pos = nodes[pos].child[c];
if (pos == -1) break;
}
return res;
}
};
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int n, m;
cin >> n >> m;
Trie trie;
vector<int> v;
for (int i = 1; i <= n; i++) {
int x; cin >> x;
v.push_back(x);
}
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for (auto x : v) trie.add_number(x);
int cur_xor = 0;
while (m--) {
int x; cin >> x;
cur_xor ^= x;
cout << trie.query(cur_xor) << "\n";
}
}Codechef - English
Đề bài
Cho $N$ xâu $W_1, W_2, \ldots, W_N$. Một cặp xâu có độ dài tiền tố chung dài nhất là $l_p$, độ dài hậu tố chung dài nhất là $l_s$, thì vẻ đẹp của cặp xâu đó là là $\min(l_p, l_s)^2$. Hãy ghép cặp các xâu, mỗi xâu nằm trong tối đa một cặp sao cho tổng vẻ đẹp các cặp xâu là lớn nhất.
Giới hạn:
- $1 \le N \le 10^5$
- $1 \le \lvert W_i \rvert \le 10^5$
- $1 \le \sum^N_{i = 1} \lvert W_i \rvert \le 10^5$
Lời giải
Giả sử bài toán định nghĩa vẻ đẹp một cặp xâu là $l_p^2$, thì bài toán có thể dễ dàng được giải quyết bằng cách dfs trên trie các xâu đã cho.
Tuy nhiên, vì đề bài định nghĩa vẻ đẹp một cặp xâu là $\min(l_p, l_s)^2$, ta cần một cách nào đó để so sánh cả tiền tố và hậu tố cùng một lúc trên trie. Ta có thể làm điều này bằng cách biến đổi các xâu $W$. Chính xác hơn, nếu $W = C_1C_2 \ldots C_M$ thì ta biến đổi $W = (C_1, C_M)(C_2, C_{M - 1}) \ldots (C_M, C_1)$ với $(C_1, C_M)$ là "kí tự" đầu tiên. Nói cách khác, ta thay đổi bảng chữ cái từ $26$ kí tự thành bảng chữ cái có $676$ kí tự $(a, a), (a, b), \ldots, (z, z)$.
Từ đó ta có thể thấy bài toán đã trở thành một cặp xâu có vẻ đẹp là $l_p^2$. Cách tính đáp án chi tiết bạn đọc có thể tham khảo trong code mẫu.
Code mẫu
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll sqr(ll x) {
return x * x;
}
struct Trie{
struct Node{
Node* child[26][26];
int cnt;
Node() {
for (int i = 0; i < 26; i++)
for (int j = 0; j < 26; j++) child[i][j] = NULL;
cnt = 0;
}
};
Node* root;
Trie() {
root = new Node();
};
void add_string(string s) {
Node* p = root;
int n = (int)s.size();
for (int i = 0; i < n; i++) {
int c1 = s[i] - 'a';
int c2 = s[n - i - 1] - 'a';
if (p->child[c1][c2] == NULL) p->child[c1][c2] = new Node();
p = p->child[c1][c2];
p->cnt++;
}
}
ll solve(Node* p, int depth) {
ll res = (p == root ? 0 : (ll)(p->cnt / 2) * (sqr(depth) - sqr(depth - 1)));
for (int c1 = 0; c1 < 26; c1++) {
for (int c2 = 0; c2 < 26; c2++) if (p->child[c1][c2] != NULL) {
res += solve(p->child[c1][c2], depth + 1);
}
}
return res;
}
};
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int t;
cin >> t;
while (t--) {
Trie trie;
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
string s;
cin >> s;
trie.add_string(s);
}
cout << trie.solve(trie.root, 0) << "\n";
}
}JOI Open Contest 2016 - Selling RNA Strands
Đề bài
Cho danh sách $N$ xâu $S_1, S_2, \ldots, S_N$ và $M$ truy vấn. Truy vấn thứ $j$ gồm hai xâu $P_j$ và $Q_j$, hãy tìm số lượng xâu trong danh sách ban đầu có tiền tố là $P_j$ và hậu tố là $Q_j$.
Giới hạn:
- $1 \le N, M, \lvert S_i \rvert, \lvert P_j \rvert, \lvert Q_j \rvert \le 10^5$
- $1 \le \sum^{N}_{i = 1} \lvert S_i \rvert \le 2 \times 10^6$.
- $1 \le \sum^{N}_{i = 1} \lvert P_j \rvert \le 2 \times 10^6$.
- $1 \le \sum^{N}_{i = 1} \lvert Q_j \rvert \le 2 \times 10^6$.
- Các xâu chỉ gồm các kí tự
A,G,C,U.
Lời giải
Đầu tiên, ta sắp xếp và đánh số lại các xâu theo thứ tự từ điển tăng dần.
Xây một trie cho $N$ xâu đó. Không khó để nhận ra rằng với mỗi đỉnh trie này, nó tương ứng với tiền tố của một đoạn liên tiếp $[l, r]$ các xâu này. Ta sẽ lưu trên mỗi đỉnh hai giá trị $l, r$ có ý nghĩa như trên.
Xây một trie thứ hai cũng cho $N$ xâu này nhưng bị đảo ngược, tức mỗi đỉnh trên trie đó tương ứng với một hậu tố của một (hoặc nhiều) xâu nào đó. Với mỗi đỉnh trên trie, ta lưu một vector chứa thứ tự của các xâu có hậu tố là xâu thể hiện bởi đỉnh đó. Lưu ý không thể lưu $l, r$ như trie trước do nó có thể không liên tiếp vì ta đã đảo ngược các xâu.
Với mỗi truy vấn $j$, ta tìm đỉnh trên trie thứ nhất thể hiện cho tiền tố $P_j$ và có được khoảng liên tiếp các xâu có tiền tố này. Tiếp theo, ta tìm đỉnh trên trie thứ hai thể hiện cho hậu tố $Q_j$ và có được vector chứa các xâu có hậu tố này. Tại đây, bài toán quy trở về cho một vector các số, tìm số số nằm trong khoảng $[l, r]$. Bài toán này có thể dễ dàng được giải quyết bằng thuật toán chặt nhị phân.
Code mẫu
#include <bits/stdc++.h>
using namespace std;
int get_val(char f) {
if (f == 'A') return 0;
if (f == 'G') return 1;
if (f == 'C') return 2;
return 3;
}
char get_char(int x) {
if (x == 0) return 'A';
if (x == 1) return 'G';
if (x == 2) return 'C';
return 'U';
}
const int NUMBEROFNODES = 2e6 + 5;
const int INF = 1e9;
struct Trie{
struct Node{
int child[4];
int l, r;
int exist;
} nodes[numberOfNodes];
int cur;
Trie() : cur(0) {
memset(nodes[0].child, -1, sizeof(nodes[cur].child));
nodes[0].l = INF; nodes[0].r = -INF;
nodes[0].exist = 0;
};
int new_node() {
cur++;
memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
nodes[cur].l = INF; nodes[cur].r = -INF;
nodes[cur].exist = 0;
return cur;
}
void add_string(string s, int id) {
int pos = 0;
for (auto f : s) {
int c = get_val(f);
if (nodes[pos].child[c] == -1) nodes[pos].child[c] = new_node();
pos = nodes[pos].child[c];
nodes[pos].l = min(nodes[pos].l, id);
nodes[pos].r = max(nodes[pos].r, id);
}
nodes[pos].exist++;
}
pair<int, int> get_range(string s) {
int pos = 0;
for (auto f : s) {
int c = get_val(f);
if (nodes[pos].child[c] == -1) return {-1, -1};
pos = nodes[pos].child[c];
}
return {nodes[pos].l, nodes[pos].r};
}
void dfs(int pos, string& current_string, vector<string>& res) {
for (int i = 1; i <= nodes[pos].exist; i++) res.push_back(current_string);
for (int i = 0; i < 4; i++) if (nodes[pos].child[i] != -1) {
current_string += get_char(i);
dfs(nodes[pos].child[i], current_string, res);
current_string.pop_back();
}
}
vector<string> sort_strings() {
vector<string> res;
string current_string = "";
dfs(0, current_string, res);
return res;
}
};
struct ReversedTrie{
struct Node{
int child[4];
vector<int> ids;
} nodes[NUMBEROFNODES];
int cur;
ReversedTrie() : cur(0) {
memset(nodes[0].child, -1, sizeof(nodes[cur].child));
nodes[0].ids.clear();
};
int new_node() {
cur++;
memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
nodes[cur].ids.clear();
return cur;
}
void add_string(string s, int id) {
reverse(s.begin(), s.end());
int pos = 0;
for (auto f : s) {
int c = get_val(f);
if (nodes[pos].child[c] == -1) nodes[pos].child[c] = new_node();
pos = nodes[pos].child[c];
nodes[pos].ids.push_back(id);
}
}
int query(string s, pair<int, int> range) {
reverse(s.begin(), s.end());
int pos = 0;
for (auto f : s) {
int c = get_val(f);
if (nodes[pos].child[c] == -1) return 0;
pos = nodes[pos].child[c];
}
int l = lower_bound(nodes[pos].ids.begin(), nodes[pos].ids.end(), range.first) - nodes[pos].ids.begin();
int r = upper_bound(nodes[pos].ids.begin(), nodes[pos].ids.end(), range.second) - nodes[pos].ids.begin() - 1;
return r - l + 1;
}
};
vector<string> sort_strings(vector<string> v) {
Trie list;
for (auto s : v) list.add_string(s, -1);
return list.sort_strings();
}
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int n, m;
cin >> n >> m;
vector<string> v;
for (int i = 1; i <= n; i++) {
string s;
cin >> s;
v.push_back(s);
}
v = sort_strings(v);
Trie trie1;
ReversedTrie trie2;
for (int i = 1; i <= n; i++) {
trie1.add_string(v[i - 1], i);
trie2.add_string(v[i - 1], i);
}
while (m--) {
string p, q;
cin >> p >> q;
pair<int, int> range = trie1.get_range(p);
if (range.first == -1) cout << "0\n";
else cout << trie2.query(q, range) << "\n";
}
}XX Open Cup, Grand Prix of Kazan - Bitwise Xor
Đề bài
Cho dãy số nguyên $a_1, a_2, \ldots, a_N$ và số nguyên $x$. Đếm số dãy con $1 \le b_1 < b_2 < \ldots < b_k \le n$ mà $a_{b_i} \oplus a_{b_j} \ge x$ với mọi cặp $(i, j)$ thỏa mãn $1 \le i < j \le k$.
Giới hạn:
- $1 \le N \le 3 \times 10^5$
- $0 \le a_i, x < 2^{60}$
Lời giải
Với một dãy số ${x_1, x_2, \ldots, x_k}$ thỏa mãn điều kiện đề bài, nhận thấy rằng nếu ta sắp xếp lại các giá trị đó từ bé đến lớn, thì giá trị bé nhất của $x_i \oplus x_j$ sẽ có $\lvert i - j \rvert = 1$. Phần chứng minh xin dành cho bạn đọc.
Vì vậy, ta có thể sắp xếp lại mảng $a$ tăng dần, và đếm số dãy $b$ thỏa mãn. Một công thức quy hoạch động với độ phức tạp $\mathcal{O}(n^2)$ khá dễ để thấy. Gọi $dp[i]$ là số dãy $b$ thỏa mãn với $b_k = i$, thì $dp[i] = \sum^{i - 1}_{j = 1,\,a_i \oplus a_j \ge x} dp[j]$.
Công thức quy hoạch động này có thể được tối ưu sử dụng một trie nhị phân. Giả dụ xét bit thứ $i$, với $i - 1$ bit đầu tiên của $a_i \oplus a_j$ bằng $i - 1$ bit đầu tiên của $x$, ta chia hai trường hợp:
- Bit thứ $i$ của $x$ là $1$: Bit thứ $i$ của $a_i \oplus a_j$ cũng phải bằng $1$. Ta đi xuống cây con tương ứng bit $1$ để xét bit thứ $i + 1$.
- Bit thứ $i$ của $x$ là $0$: Bit thứ $i$ của $a_i \oplus a_j$ có thể là $0$ hoặc $1$. Nếu là $1$ thì các bit còn lại ta điền gì cũng vẫn thỏa mãn $a_i \oplus a_j \ge x$, tức có thể lấy tổng tất cả giá trị $dp$ trong cây con tương ứng bit $1$. Rồi ta đi xuống cây con tương ứng bit $0$ để xét bit thứ $i + 1$.
Dựa vào bit thứ $i$ của $a_i \oplus a_j$ và giá trị của $a_i$ ta hoàn toán có thể tính được bit thứ $i$ của $a_j$. Lưu ý mọi dãy con gồm $1$ phần tử đều thỏa mãn điều kiện của đề bài.
Lúc này, bạn đọc có thể tưởng tượng trie như một cây phân đoạn, truy vấn trên trie y hệt như truy vấn như cây phân đoạn nhưng điều kiện đi xuống cây con bên nào bị thay đổi.
Code mẫu
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MOD = 998244353;
void add(int& a, int b) {
if ((a += b) >= MOD) a -= MOD;
}
const int NUMBEROFNODES = 18000005;
const int LG = 60;
struct Trie{
struct Node{
int child[2];
int sum;
} nodes[NUMBEROFNODES];
int cur;
Trie() : cur(0) {
memset(nodes[0].child, -1, sizeof(nodes[cur].child));
nodes[0].sum = 0;
};
int new_node() {
cur++;
memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
nodes[cur].sum = 0;
return cur;
}
void add_value(ll x, int val) {
int pos = 0;
for (int i = LG; i >= 0; i--) {
int c = (x >> i) & 1;
if (nodes[pos].child[c] == -1) nodes[pos].child[c] = new_node();
pos = nodes[pos].child[c];
add(nodes[pos].sum, val);
}
}
int query(ll x, ll k) {
int pos = 0, res = 0;
for (int i = LG; i >= 0; i--) {
int c1 = (x >> i) & 1;
int c2 = (k >> i) & 1;
if (c2 == 1) {
if (nodes[pos].child[c1 ^ 1] == -1) break;
pos = nodes[pos].child[c1 ^ 1];
}
else {
if (nodes[pos].child[c1 ^ 1] != -1) add(res, nodes[nodes[pos].child[c1 ^ 1]].sum);
if (nodes[pos].child[c1] == -1) break;
pos = nodes[pos].child[c1];
}
if (i == 0) add(res, nodes[pos].sum);
}
return res;
}
};
const int N = 3e5 + 5;
int n;
ll k;
ll a[N];
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + n + 1);
Trie trie;
int res = n;
for (int i = 1; i <= n; i++) {
int val = trie.query(a[i], k);
trie.add_value(a[i], val + 1);
add(res, val);
}
cout << res;
}Bài tập
Trie xâu
Codechef - Query On Strings (Dễ)
Codeforces Gym - Know Your Statement (Trung bình)
Codechef - Paisa Double (Trung bình)
VOI 2021 - Phần thưởng (Trung bình)
Atcoder - Prefix-tree Game (Khó)
PVHOI 2.2 - Tiền tố chung dài nhất (Khó)
Trie nhị phân
Hackerrank - XOR Key (Dễ)
SPOJ - SubXor (Dễ)
SPOJ - x-Xor It! (Dễ)
CSAcademy - Xor Submatrix (Trung bình)
HDU - I love counting (Trung bình)