Nguồn: wcipeg, cp-algorithms, Tất tần tật về Cây Phân Đoạn (Segment Tree) - VNOI

Tác giả:

Nguyễn Châu Khanh - VNU University of Engineering and Technology (VNU-UET)

Reviewer:

Trần Xuân Bách - HUS High School for Gifted Students
Nguyễn Nhật Minh Khôi - VNUHCM-University of Science
Nguyễn Phú Bình - Hung Vuong High School for the Gifted, Binh Duong Province
Ngô Nhật Quang - HUS High School for Gifted Students
Hồ Ngọc Vĩnh Phát - VNUHCM-University of Science

LƯU Ý: Mọi số thứ tự trong bài viết đều được đánh số bắt đầu từ $1$.

Mở đầu

Cây phân đoạn (Segment Tree) là một cấu trúc dữ liệu rất linh hoạt được sử dụng nhiều trong các kỳ thi, đặc biệt là trong những bài toán xử lý trên dãy số.

Ở bài viết này, ta sẽ chỉ tìm hiểu về những kiến thức cơ bản của Segment Tree và một số bài tập thường gặp trong các kì thi.

Còn nếu bạn muốn tìm hiểu sâu hơn về Segment Tree thì bạn có thể tham khảo bài viết: Tất tần tật về Cây Phân Đoạn (Segment Tree) - VNOI.

Ý tưởng

Một trong những ứng dụng phổ biến nhất của Segment Tree là giải quyết bài toán $Range \space Minimum \space Query \space \mathit{(RMQ)}$. Trong bài toán này, ta được cho một mảng $A$ và $Q$ truy vấn; mỗi truy vấn gồm cặp số $l$ và $r$, yêu cầu tìm phần tử có giá trị nhỏ nhất trong đoạn từ $l$ đến $r$ của mảng $A$.

Ví dụ: Ta có mảng $A = \{9,2,6,3,1,5,7\}$. Với truy vấn $l = 3$ và $r = 6$, đáp án sẽ là $\min{(6,3,1,5)} = 1$. Sau đó, một truy vấn khác với $l = 1$ và $r = 3$ thì đáp án là $2$; v.v…

Có nhiều giải pháp khác nhau để giải quyết bài toán này nhưng Segment Tree thường là lựa chọn thích hợp nhất, đặc biệt là khi có thêm hoạt động sửa đổi được xen kẽ với các truy vấn.

Giải pháp chia để trị

Ta có giải pháp chia để trị sau:
- Nếu dãy đang xét chứa một phần tử, thì bản thân phần tử đó là giá trị nhỏ nhất trong dãy đó.
- Nếu không, ta chia dãy đó thành hai dãy con liên tiếp nhỏ hơn, mỗi dãy con gần bằng một nửa kích thước của dãy ban đầu, và tìm giá trị nhỏ nhất tương ứng của chúng. Giá trị nhỏ nhất của dãy ban đầu chính là giá trị nhỏ hơn giữa hai giá trị nhỏ nhất của các dãy con.
  - Ví dụ mô tả thuật toán chia để trị với mảng $A = \{9,2,6,3,1,5,7\}$:
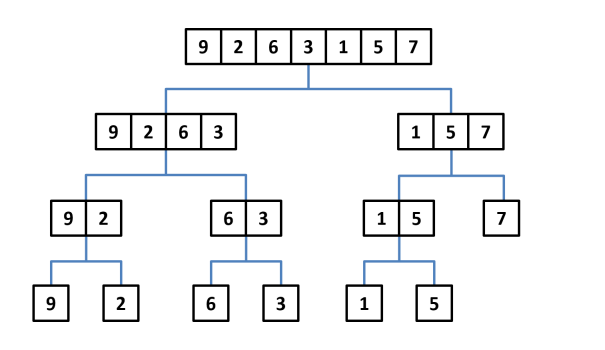
Nhận thấy rằng, khi ta sửa đổi giá trị của một phần tử bất kỳ trong mảng thì số lượng đoạn cần tính lại không nhiều. Vậy nên ta sẽ lưu lại kết quả và chỉ tính lại khi thực sự cần thiết.
- Ví dụ: Trong ví dụ bên trên, khi sửa đổi phần tử có giá trị $1$ thành giá trị $8$ thì ta chỉ cần tính lại giá trị nhỏ nhất của các đoạn $[1, 7]$, $[5, 7]$, $[5, 6]$ và $[5, 5]$.

Tổng quát

Gọi $a_i$ là giá trị của phần tử thứ $i$ trong mảng, việc tìm giá trị nhỏ nhất có thể được viết dưới dạng hàm đệ quy như sau: $f(l, r) = \begin{cases} a_l & \quad \text{if } l = r \\ \min{\Big( f \big(l, \big\lfloor \frac{l + r}{2} \big\rfloor \big), f \big( \big\lfloor \frac{l + r}{2} \big\rfloor + 1, r \big) \Big)} & \quad \text{if } l < r \end{cases}$
- Với $f(l, r)$ là phần tử có giá trị nhỏ nhất trong đoạn từ $l$ đến $r$ của mảng $A$.
Do đó, khi ta sửa đổi giá trị của phần tử thứ $i$ trong mảng thì ta chỉ cần tính lại kết quả của các hàm $f(l, r)$ với $l \le i \le r$.

Giả sử rằng ta sử dụng hàm được định nghĩa ở trên để xác định $f(1, N)$, với $N$ là số lượng phần tử của mảng. Khi $N$ lớn, hàm gọi đệ quy này sẽ có hai "con", một trong số đó là lệnh gọi đệ quy $f \big(l, \big\lfloor \frac{l + r}{2} \big\rfloor \big)$ và lệnh còn lại là $f \big( \big\lfloor \frac{l + r}{2} \big\rfloor + 1, r \big)$. Mỗi hàm này sau đó sẽ lại có thêm hai "con" của riêng nó, và cứ tiếp tục như vậy cho đến khi đạt được trường hợp cơ sở (khi $l = r$).

Nếu ta biểu diễn các hàm gọi đệ quy này bằng cấu trúc cây, thì hàm $f(1, N)$ sẽ là gốc, nó sẽ có hai con, mỗi con sẽ có thêm hai con nữa, v.v…; các trường hợp cơ sở sẽ là lá của cây. Khi đó, cấu trúc cây gọi đệ quy của hàm $f(1, N)$ chính là cấu trúc của cây phân đoạn. Và việc sửa đổi giá trị phần tử trong mảng cũng chính là bản chất của thao tác cập nhật trên cây phân đoạn (sẽ được mô tả rõ hơn ở phần sau).

Ví dụ: Ta có mảng $A = \{9,2,6,3,1,5,7\}$ được kiểm soát bởi cây phân đoạn sau:

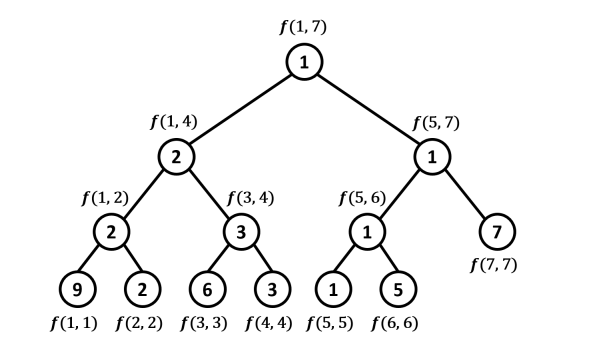
Cấu trúc

Bây giờ ta đã sẵn sàng để xác định cấu trúc của cây phân đoạn:

Segment Tree là một cây. Cụ thể hơn, nó là một cây nhị phân đầy đủ (mỗi nút là lá hoặc có đúng $2$ nút con).
Mỗi nút quản lý một dãy các đối tượng liên tiếp, trong nút chứa thông tin tổng hợp từ các đối tượng mà nó quản lý.
Với một dãy số gồm $N$ phần tử, nút gốc quản lý các đối tượng từ $1$ tới $N$.
Nếu một nút quản lý dãy các đối tượng từ $l$ tới $r$ $(l<r)$ thì nút con trái của nó quản lý các đối tượng từ $l$ tới $mid$ và nút con phải của nó quản lý các đối tượng từ $mid+1$ tới $r$ $\big($Với $mid = \big\lfloor \frac{l + r}{2} \big\rfloor \big)$.
Nếu một nút chỉ quản lý một đối tượng thì nó sẽ là nút lá và không có nút con.
Chiều cao của cây phân đoạn là $\mathcal{O}(\log{N})$, bởi vì khi đi xuống từ gốc đến lá, kích thước của mỗi đoạn giảm đi một nửa.
Tại mỗi độ sâu của cây, không có phần tử nào được quản lý bởi $2$ nút khác nhau của cây.

Các thao tác trên cây phân đoạn

Có $3$ thao tác cơ bản trên cây phân đoạn:

Xây dựng

Để có thể có thể lấy giá trị và sửa đổi dãy số, trước tiên ta cần phải xây dựng một cây phân đoạn hợp lệ.

Trước khi xây dựng cây phân đoạn, ta cần quyết định:

Thông tin được lưu trữ tại mỗi nút của cây phân đoạn. Ví dụ: Trong cây phân đoạn lấy giá trị nhỏ nhất, một nút sẽ lưu trữ giá trị nhỏ nhất của các phần tử trong đoạn $[l, r]$ mà nó quản lý.
Phép toán hợp nhất hai nút con trong một cây phân đoạn. Ví dụ: Trong cây phân đoạn lấy giá trị nhỏ nhất, hai nút con tương ứng với đoạn $[l1, r1]$ và đoạn $[l2, r2]$ sẽ được hợp nhất thành một nút tương ứng với đoạn $[l1, r2]$ bằng cách lấy min các giá trị của hai nút con.

$\circ$ Lưu ý rằng một đỉnh là "đỉnh lá", nếu đoạn tương ứng của nó chỉ bao gồm một giá trị trong mảng ban đầu. Nó là đỉnh thấp nhất của cây phân đoạn. Giá trị của nó sẽ bằng phần tử $a_i$ tương ứng.

Có $2$ cách để xây dựng một cây phân đoạn:

Cách 1: Xây dựng "từ dưới lên trên"
- Để xây dựng cây phân đoạn, ta sẽ bắt đầu ở các nút có độ sâu thấp nhất (các nút lá) và gán cho chúng các giá trị tương ứng. Rồi từ đó, ta có thể tính toán lên các nút cha bằng cách "hợp nhất" lần lượt $2$ nút con và lặp lại quy trình cho đến khi đạt đến đỉnh gốc.
Cách 2: Xây dựng "từ trên xuống dưới"
- Cấu trúc từ trên xuống là sử dụng đệ quy. Tức là ta sẽ bắt đầu từ đỉnh gốc đến các đỉnh lá bằng mô hình đệ quy như sau:
  1. Nếu nút đang xét là nút lá, ta có thể lấy được ngay giá trị tương ứng từ mảng.
  2. Ngược lại, nếu nút đang xét không phải là nút lá, ta gọi đệ quy để tính toán giá trị của hai nút con. Sau khi hai lệnh gọi đệ quy được thực hiện, giá trị của nút đang xét sẽ bằng giá trị được "hợp nhất" từ hai nút con.
- Do thủ tục đệ quy bắt đầu từ đỉnh gốc nên ta có thể tính toán được toàn bộ cây phân đoạn.

Cập nhật

Bây giờ ta muốn sửa đổi một phần tử cụ thể trong mảng, giả sử ta muốn thực hiện việc gán $a_i = x$. Và phải cập nhật lại cây phân đoạn, sao cho nó tương ứng với mảng mới đã sửa đổi.

Để làm như vậy, trước tiên ta cần sửa đổi nút lá tương ứng. Các nút lá khác không bị ảnh hưởng, vì mỗi nút lá chỉ được liên kết với một phần tử trong mảng. Nút cha của nút đã sửa đổi cũng bị ảnh hưởng, vì đoạn nó quản lý cũng chứa phần tử đã sửa đổi, và các nút tổ tiên của nó cũng vậy, v.v… cho đến nút gốc.

Nói cách khác, tất cả các nút nằm trên đường đi đơn từ gốc đến nút lá tương ứng đều bị ảnh hưởng. Ngoài ra, không còn nút nào khác bị ảnh hưởng. Do đó, với một dãy số gồm $N$ phần tử thì chiều cao của cây phân đoạn tương ứng sẽ là $\mathcal{O}(\log{N})$ nên chỉ có $\mathcal{O}(\log{N})$ nút cần được cập nhật.

Ví dụ: Cho mảng $A = \{9,2,6,3,1,5,7\}$. Phần tử có giá trị $1$ được thay đổi thành giá trị $8$ trong cây phân đoạn lấy giá trị nhỏ nhất.

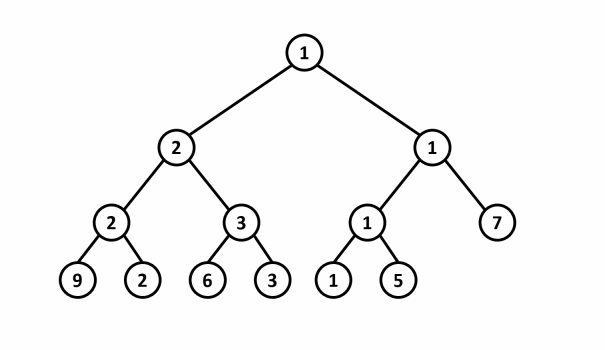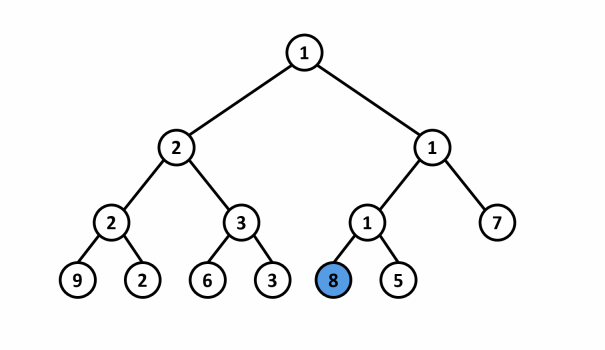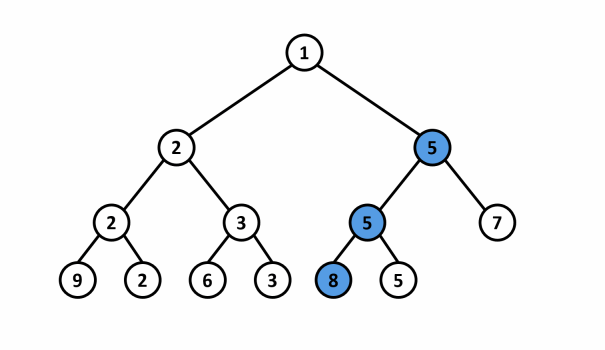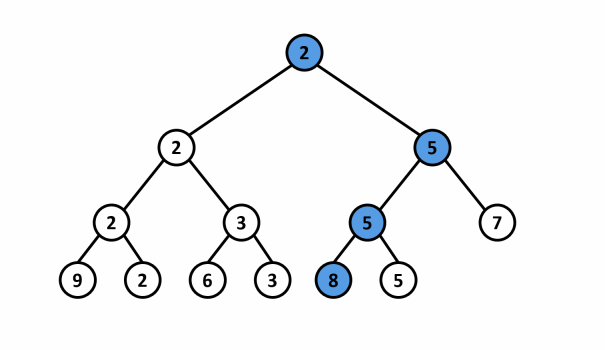
Thao tác cập nhật cây phân đoạn có thể được thực hiện bằng cách sử dụng một hàm đệ quy:

Để thực hiện cập nhật từ trên xuống, ta bắt đầu từ nút gốc; điều này dẫn đến lệnh gọi đệ quy tới một nút con quản lí đoạn chứa phần tử cần sửa đổi (nút con còn lại và cây con của nó không bị ảnh hưởng); v.v… Cho đến trường hợp cơ sở là nút lá được liên kết với phần tử cần cập nhật, ta sửa lại giá trị của nút lá đó.
Sau khi hoàn tất lệnh gọi đệ quy cho các nút con (trừ trường hợp cơ sở), giá trị của nút đang xét sẽ được cập nhật lại theo giá trị hai nút con của nó.

Tương tự như thao tác xây dựng cây phân đoạn, cách cập nhật cây phân đoạn "từ dưới lên" cũng có thể thực hiện được.

Lấy giá trị

Bây giờ, ta cần phải trả lời các truy vấn lấy giá trị. Ví dụ như: cho hai số nguyên $l$ và $r$, hãy xác định phần tử có giá trị nhỏ nhất trong đoạn $[l, r]$ của mảng $A$ với khoảng thời gian là $\mathcal{O}(\log{n})$.

Do thao tác lấy giá trị này phức tạp hơn thao tác cập nhật cây phân đoạn nên ta sẽ lấy một ví dụ minh họa để dễ hình dung:

Giả sử, cho mảng $A = \{9,2,6,3,1,5,7\}$ và ta muốn biết phần tử nhỏ nhất trong đoạn $[1, 6]$ của mảng $A$.

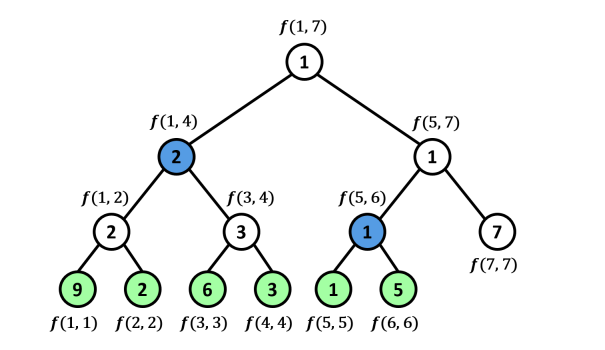
Gọi $f(l,r)$ là phần tử có giá trị nhỏ nhất trong đoạn $[l, r]$. Ta thấy rằng mỗi nút trong cây phân đoạn đều quản lí một đoạn nào đó, ví dụ như nút gốc chứa $f(1,7)$, nút con bên trái là $f(1,4)$, nút bên phải là $f(5,7)$, v.v…; và mỗi nút lá chứa $f(i, i) = a_i$. Nhưng không có nút nào chứa $f(1,6)$; tuy nhiên, ta nhận thấy rằng $f(1,6) = \min{(f (1,4), f (5,6))}$, và có tồn tại các nút trong cây phân đoạn chứa hai giá trị đó (được hiển thị bằng màu xanh dương trong hình trên).

Dễ thấy rằng $f (x, y) = \min{(f(x, z), f(z + 1, y)})$ với $x \le z < y$. Do đó, ta phải xác định tập hợp ít nút nhất sao cho tổng tất cả các phạm vi mà các nút đó quản lí đúng bằng đoạn cần truy vấn. Sự kết hợp của tập hợp các nút đó chính xác là đáp án mà ta tìm kiếm.

Để làm như vậy, ta sẽ bắt đầu từ gốc và đệ quy qua các nút mà phạm vi quản lí của nó có ít nhất một phần tử chung với đoạn cần truy vấn.

Trong ví dụ trên với $f(1,6)$, xét hai nút con của gốc, ta nhận thấy rằng cả nút con bên trái và bên phải đều quản lí một số các phần tử con thuộc đoạn cần truy vấn (đoạn $[1, 6]$). Do đó, ta sẽ thực hiện lệnh gọi đệ quy trên cả hai nút con của nút gốc. Khi đó, nút con bên trái của gốc đóng vai trò như một trường hợp cơ sở, vì phạm vi quản lí của nó được chứa hoàn toàn bên trong đoạn truy vấn; vậy nên nó được chọn (đánh dấu bằng màu xanh dương).

Còn với nút con bên phải của gốc (nút chứa $f(5, 7)$); ta nhận thấy rằng nút con bên trái của nút $f(5, 7)$, tức là $f(5, 6)$ có quản lí một số các phần tử con thuộc đoạn cần truy vấn, nhưng nút con bên phải là $f(7, 7)$ thì không. Vì vậy, ta chỉ tiếp tục gọi đệ quy trên nút con bên trái là nút chứa $f(5, 6)$ và bỏ qua không gọi đệ quy nút con bên phải là nút chứa $f(7, 7)$.

Khi đấy, nút con bên trái đó (nút $f(5, 6)$) sẽ là một trường hợp cơ sở khác, nó cũng được chọn (và đánh dấu bằng màu xanh dương).

Đệ quy kết thúc và giá trị nhỏ nhất của đoạn cần truy vấn chính là giá trị nhỏ nhất của các nút đã được chọn.

Cài đặt

Thứ khiến ta cần phải cân nhắc ở đây chính là cách lưu trữ cây phân đoạn. Tất nhiên, ta có thể tạo ra một cấu trúc cây và danh sách cạnh, lưu trữ phạm vi quản lí của từng nút và các thông tin của nó. Tuy nhiên điều này đòi hỏi phải lưu trữ nhiều thông tin dư thừa.

Thay vào đó, ta sẽ sử dụng một thủ thuật đơn giản để làm cho việc này trở nên hiệu quả hơn rất nhiều. Ta sẽ chỉ lưu trữ các thông tin của từng nút vào trong một mảng. Thông tin của nút gốc lưu ở chỉ số $1$, thông tin của hai nút con của nó lưu ở chỉ số $2$ và $3$, thông tin của các nút con của hai nút đó sẽ lưu ở chỉ số từ $4$ đến $7$, v.v… Dễ dàng nhận thấy, con bên trái của nút có chỉ số $id$ được lưu trữ tại chỉ số $2 \times id$ và con bên phải được lưu trữ tại chỉ số $2 \times id + 1$.

Ví dụ minh họa: Cho mảng $A = \{9,2,6,3,1,5,7\}$, ta có $st[] = \{1, 2, 1, 2, 3, 1, 7, 9, 2, 6, 3, 1, 5\}$ (với $st[]$ là mảng biểu diễn cho Segment Tree, lưu lại thông tin của mỗi nút).
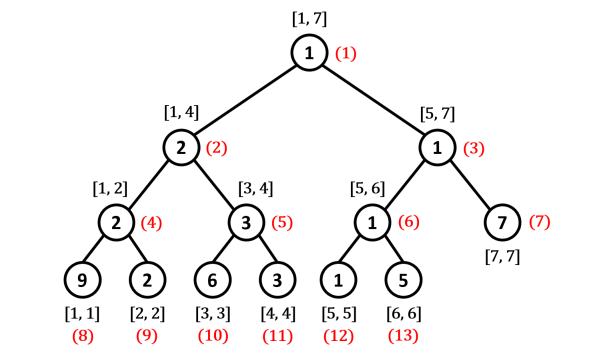
- Chỉ số trên mảng được viết bằng màu đỏ bên cạnh mỗi nút, ví dụ như nút có chỉ số $id = 2$ sẽ quản lí đoạn $[1, 4]$ và nút con bên trái của nó có chỉ số $4$, còn nút con bên phải có chỉ số $5$.

Điều này đơn giản hóa việc cài đặt rất nhiều. Ta không cần lưu hết toàn bộ cấu trúc của cây trong bộ nhớ. Mà nó sẽ được định nghĩa một cách ngầm định. Ta chỉ cần một mảng chứa thông tin của tất cả các phân đoạn.

Để dễ hình dung, ta lấy $1$ ví dụ cụ thể:

Cho dãy $A$ gồm $n$ phần tử $a_1, a_2, …, a_n$ $(1 \le n \le 10^5; \space |a_i| \le 10^9$ với $1 \le i \le n)$.
Có $q$ truy vấn $(1 \le q \le 10^5)$. Mỗi truy vấn thuộc $1$ trong $2$ loại:
- Loại 1: Có dạng $1 \space x \space y$ : Gán giá trị $y$ cho phần tử ở vị trí $x$.
- Loại 2: Có dạng $2 \space l \space r$ : Tìm phần tử có giá trị nhỏ nhất trong đoạn $[l, r]$.

Cách đơn giản nhất là dùng một mảng $A$ duy trì giá trị các phần tử. Với truy vấn $1$ thì ta gán $A[x] = y$. Với truy vấn $2$ thì ta dùng một vòng lặp từ $l$ đến $r$ để tìm giá trị nhỏ nhất. Rõ ràng cách này có độ phức tạp là $\mathcal{O}(n \times q)$ và không thể chạy trong thời gian cho phép.

Do đó, ta sẽ cài đặt Segment Tree để giải quyết bài toán trên như sau:

Cấu trúc dữ liệu:

Hằng số maxN = 100007 .
Hằng số inf = 1000000007 .
Mảng st[] - Lưu thông tin của mỗi nút trên Segment Tree.

#include <bits/stdc++.h>

using namespace std;

const int inf  = 1e9 + 7;
const int maxN = 1e5 + 7;

int n, q;
int a[maxN];
int st[4 * maxN]; // Lí do sử dụng kích thước mảng là 4 * maxN sẽ được giải thích ở phần sau

// Thủ tục xây dựng cây phân đoạn
void build(int id, int l, int r) {
    // Đoạn chỉ gồm 1 phần tử, không có nút con
    if (l == r) {
        st[id] = a[l];
        return;
    }

    // Gọi đệ quy để xử lý các nút con của nút id
    int mid = l + r >> 1; // (l + r) / 2
    build(2 * id, l, mid);
    build(2 * id + 1, mid + 1, r);
    
    // Cập nhật lại giá trị min của đoạn [l, r] theo 2 nút con
    st[id] = min(st[2 * id], st[2 * id + 1]);
}

// Thủ tục cập nhật
void update(int id, int l, int r, int i, int val) {
    // i nằm ngoài đoạn [l, r], ta bỏ qua nút id
    if (l > i || r < i) return;
    
    // Đoạn chỉ gồm 1 phần tử, không có nút con
    if (l == r) {
        st[id] = val;
        return;
    }
    
    // Gọi đệ quy để xử lý các nút con của nút id
    int mid = l + r >> 1; // (l + r) / 2
    update(2 * id, l, mid, i, val);
    update(2 * id + 1, mid + 1, r, i, val);
    
    // Cập nhật lại giá trị min của đoạn [l, r] theo 2 nút con
    st[id] = min(st[2 * id], st[2 * id + 1]);
}


// Hàm lấy giá trị
int get(int id, int l, int r, int u, int v) {
    // Đoạn [u, v] không giao với đoạn [l, r], ta bỏ qua đoạn này
    if (l >  v || r <  u) return inf; 
    
    /* Đoạn [l, r] nằm hoàn toàn trong đoạn [u, v] mà ta đang truy vấn, 
        ta trả lại thông tin lưu ở nút id */
    if (l >= u && r <= v) return st[id];

    // Gọi đệ quy với các nút con của nút id
    int mid = l + r >> 1; // (l + r) / 2
    int get1 = get(2 * id, l, mid, u, v);
    int get2 = get(2 * id + 1, mid + 1, r, u, v);
    
    // Trả ra giá trị nhỏ nhất theo 2 nút con
    return min(get1, get2);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);

    cin >> q;
    while (q--) {
        int type, x, y;
        cin >> type >> x >> y;
        if (type == 1) update(1, 1, n, x, y); // Gán giá trị y cho phần tử ở vị trí x 
        else cout << get(1, 1, n, x, y) << '\n'; // In ra giá trị nhỏ nhất trong đoạn [x, y]
    }
}

Đánh giá

Ở phần Các thao tác trên cây phân đoạn có nhắc đến $2$ cách để cài đặt Segment Tree. Vì sự khác biệt về tốc độ của hai cách có thể là không đáng kể, nên bài viết này sẽ chỉ cài đặt theo cách thông thường nhất là sử dụng phương pháp đệ quy.

Segment Tree còn có một cách cài đặt khác sử dụng ít bộ nhớ hơn (sử dụng tối đa $2 \times N$ phần tử), cài đặt ngắn hơn và chạy nhanh hơn. Tuy nhiên thì nó không dễ hiểu bằng cách cài đặt trên. Bạn có thể tham khảo thêm tại đây: VNOI - Efficient and easy segment trees.

Phân tích độ phức tạp

Bộ nhớ

Ta xét $2$ trường hợp:

TH1: $N = 2^k$ : Cây phân đoạn đầy đủ, ở độ sâu cuối cùng có đúng $2^k$ lá, và các độ sâu thấp hơn không có nút lá nào (và các nút này đều có đúng $2$ con). Như vậy:
- Tầng $k$ : có $2^k$ nút
- Tầng $k-1$ : có $2^{k-1}$ nút
- … $\Rightarrow$ Tổng số nút không quá $2^{k+1}$ (vì tổng số nút $= 2^k + 2^{k-1} + \ldots + 2^0 = 2^{k+1} - 1$ theo công thức cấp số nhân).
TH2: Với $N > 2^k$ và $N < 2^{k+1}$ : Số nút của cây phân đoạn không quá số nút của cây phân đoạn với $N = 2^{k+1}$.

Do đó, số nút của cây cho dãy $N$ phần tử (với $N \le 2^k$) là không quá $2^{k+1}$, giá trị này xấp xỉ $4 \times N$. Bằng thực nghiệm, ta thấy dùng $4 \times N$ là đủ.

Tham khảo thêm các cách chứng minh khác tại đây: Codeforces – Blog entry 49939.

Thời gian

Thao tác xây dựng

Thao tác xây dựng sẽ yêu cầu một số lượng hoạt động không đổi trên mỗi nút của cây phân đoạn. Với mảng có $N$ phần tử thì số lượng nút của cây phân đoạn xấp xỉ $4 \times N$ (đã chứng minh ở trên), và vì thao tác xây dựng mất thời gian tuyến tính nên sẽ có độ phức tạp là $\mathcal{O}(4 \times N)$.

Ta có thể nhận thấy rằng thao tác xây dựng nhanh hơn so với việc thực hiện các thao tác cập nhật riêng biệt (việc duyệt từng phần tử của mảng để cập nhật sẽ mất độ phức tạp $\mathcal{O}(N \times \log{N})$ ).

Thao tác cập nhật

Với thao tác cập nhật, một số lượng các hoạt động không đổi được thực hiện cho mỗi nút trên đường đi đơn từ gốc đến nút lá tương ứng với phần tử cần sửa đổi. Đồng nghĩa với việc ở mỗi độ sâu của cây, ta chỉ gọi đệ quy tới không quá $1$ nút con.

Phân tích đoạn code trên, ta xét các trường hợp:

Phần tử cần xét không nằm trong đoạn $[l, r]$ do nút $id$ quản lý. Trường hợp này ta dừng lại, không xét tiếp.
Phần tử cần xét nằm trong đoạn $[l, r]$ do nút $id$ quản lý. Ta xét các con của nút $id$. Tuy nhiên chỉ có $1$ con của nút $id$ chứa phần tử cần xét và ta sẽ phải xét tiếp các con của nút này. Với nút con còn lại, ta sẽ dừng ngay mà không xét các con của nó nữa.

Vì số lượng các nút trên đường đi đơn từ gốc đến nút lá tương ứng được giới hạn bởi chiều cao của cây là $\mathcal{O}(\log{N})$ nên độ phức tạp của thao tác cập nhật sẽ là $\mathcal{O}(\log{N})$.

Thao tác lấy giá trị

Trước tiên, ta hãy xem xét từng độ sâu của của cây. Từ đó có thể thấy rằng đối với mỗi độ sâu, ta chỉ truy cập không quá $4$ nút. Và vì chiều cao của cây là $\mathcal{O}(\log{N})$ nên độ phức tạp của thao tác lấy giá trị là $\mathcal{O}(\log{N})$.

Ta có thể chứng minh rằng mệnh đề này (truy cập nhiều nhất bốn nút trong mỗi độ sâu) là đúng bằng phương pháp quy nạp:

Ở độ sâu đầu tiên, ta chỉ truy cập duy nhất một nút là nút gốc, vì vậy ở đây ta truy cập ít hơn $4$ nút.
Bây giờ, ta hãy xem xét một độ sâu bất kì. Theo giả thuyết quy nạp là ta thăm nhiều nhất $4$ nút. Nếu ta chỉ thăm nhiều nhất $2$ nút, thì ở độ sâu tiếp theo, số lượng nút được thăm nhiều nhất sẽ là $4$ nút. Điều đó thật hiển nhiên, bởi vì mỗi nút có thể tạo ra nhiều nhất $2$ lệnh gọi đệ quy.
Vì vậy, giả sử rằng ta truy cập $3$ hoặc $4$ nút trong độ sâu hiện tại. Từ các nút đó, ta sẽ phân tích kỹ hơn các nút nằm ở giữa (nghĩa là nút thứ hai từ trái sang với số lượng nút đang được truy cập là $3$ và nút thứ $2, \space 3$ với số nút đang được truy cập là $4$) . Vì truy vấn yêu cầu lấy giá trị của một đoạn con liên tục, ta biết rằng các phân đoạn tương ứng với các nút đã thăm ở giữa sẽ được bao phủ hoàn toàn bởi phân đoạn của truy vấn. Do đó các nút này sẽ không thực hiện bất kỳ lệnh gọi đệ quy nào tới các nút con nữa. Vì vậy, chỉ nút bên trái nhất và nút bên phải nhất mới có khả năng tiếp tục gọi đệ quy. Và hai nút đó sẽ chỉ tạo ra nhiều nhất $4$ lệnh gọi đệ quy, vì vậy độ sâu tiếp theo cũng sẽ đáp ứng đúng mệnh đề.
- Ví dụ: Giả sử, đoạn cần truy vấn là đoạn $[2, 5]$. Ở độ sâu thứ $3$, ta sẽ truy cập vào ba nút quản lí các đoạn $[1, 2]$, $[3, 4]$ và $[5, 6]$ (được đánh dấu bằng màu xanh dương). Khi đó, vì nút quản lí đoạn $[3, 4]$ nằm hoàn toàn bên trong đoạn $[2, 5]$ nên hàm đệ quy sẽ trả ra luôn giá trị của nút đó, mà không gọi đệ quy tới các nút con. Chỉ có hai nút là nút bên trái nhất quản lí đoạn $[1, 2]$ và nút bên phải nhất quản lí đoạn $[5, 6]$ mới được tiếp tục gọi đệ quy.
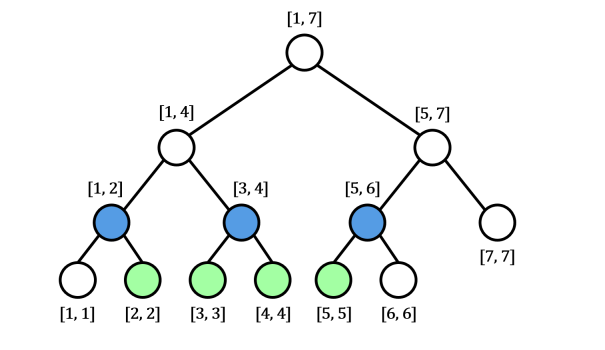
Ta cũng có thể nói rằng một nhánh cây phân đoạn sẽ tiếp cận dần tới giới hạn bên trái của truy vấn và nhánh thứ hai tiếp cận tới giới hạn bên phải.

Do đó, ta sẽ chỉ truy cập nhiều nhất $4 \times \log{N}$ nút trên cây phân đoạn, và đó cũng chính là độ phức tạp của thao tác lấy giá trị.

Ví dụ 1

VNOI - ITEZ2

Bài toán

Bạn được cho một mảng gồm $n$ số nguyên. Ban đầu tất cả các số của mảng đều là $0$. Nhiệm vụ của bạn là xử lí $2$ loại truy vấn:

Loại $1$ có dạng $1 \space x \space y$ : Gán phần tử ở vị trí thứ $x$ trong dãy thành số $y$ $(1 \le x \le n, |y| \le 10^9)$.
Loại $2$ có dạng $2 \space l \space r$ : In ra tổng các phần tử trong đoạn từ $l$ đến $r$ $(1 \le l \le r \le n)$.

Với mỗi truy vấn loại $2$, hãy in ra câu trả lời trên một dòng.

$\circ \space \space 1 \le n, q \le 10^5$ (với $q$ là số lượng truy vấn).

Phân tích

Vì ban đầu giá trị của tất cả phần tử trong mảng đều bằng $0$ nên ta không cần phải thực hiện thao tác xây dựng cây phân đoạn.

Nhận thấy rằng, trên cây phân đoạn, mỗi nút không phải lá sẽ chứa tổng giá trị tại các nút con của nó. Do đó, ta chỉ cần thay thế tất cả các phép toán min ở ví dụ trên (trong phần Cài đặt) bằng các phép toán cộng.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 100007.
Mảng st[] - Lưu thông tin của mỗi nút trên Segment Tree.

#include <bits/stdc++.h>

using namespace std;

const int maxN = 1e5 + 7;

int n, q;
int a[maxN];
long long st[4 * maxN];

// Thủ tục cập nhật
void update(int id, int l, int r, int i, int val) {
    if (l > i || r < i) return;
    if (l == r) {
        st[id] = val;
        return;
    }
    int mid = l + r >> 1;
    update(2 * id, l, mid, i, val);
    update(2 * id + 1, mid + 1, r, i, val);
    st[id] = st[2 * id] + st[2 * id + 1];
}

// Hàm lấy tổng giá trị
long long get(int id, int l, int r, int u, int v) {
    if (l >  v || r <  u) return 0;
    if (l >= u && r <= v) return st[id];

    int mid = l + r >> 1;
    long long get1 = get(2 * id, l, mid, u, v);
    long long get2 = get(2 * id + 1, mid + 1, r, u, v);
    return get1 + get2;
}

int main() {
    cin >> n >> q;
    while (q--){
        int type, x, y;
        cin >> type >> x >> y;
        if (type == 1) update(1, 1, n, x, y);
        else cout << get(1, 1, n, x, y) << '\n';
    }
}

Đánh giá

Độ phức tạp

Với mỗi truy vấn, ta sẽ mất $\mathcal{O}(\log{n})$ cho mỗi thao tác trên Segment Tree. Do đó, độ phức tạp của thuật toán là $\mathcal{O}(q \times \log{n})$.

Ví dụ 2

VNOI - GSS

Bài toán

Cho dãy số $a_1, a_2, …, a_n$ $(|a_i| \le 15000, \space n \le 50000)$.

Hàm $q(x, y)$ = $\max \Big( \displaystyle\sum_{k = i}^{j} a_k$, với $x \le i \le j \le y \Big)$.

Cho $m$ $(m \le 50000)$ câu hỏi dạng $x, y$ $(1 \le x \le y \le n)$, hãy tính các $q(x, y)$.

Phân tích

Ở bài toán này, mỗi nút của cây phân đoạn lưu lại các thông tin sau:

pre : Tiền tố có tổng giá trị lớn nhất trên đoạn.
suf : Hậu tố có tổng giá trị lớn nhất trên đoạn.
sum : Tổng giá trị các phần tử trên đoạn.
maxsum : Tổng giá trị lớn nhất của đoạn con nằm trong đoạn mà nút đó quản lí.

Bây giờ, ta cần phải xác định các phép toán để "hợp nhất" hai nút con:

pre : Dễ thấy rằng tiền tố lớn nhất của nút cha sẽ bằng max tiền tố của nút con bên trái và tổng giá trị của nút con bên trái cộng với tiền tố của nút con bên phải.
- Minh họa: $\mathrm{pre}[l, r] = \max{(\mathrm{pre}[l, mid], \space \mathrm{sum}[l, mid] + \mathrm{pre}[mid + 1, r])}$ với $mid = \big\lfloor \frac{l + r}{2} \big\rfloor$.
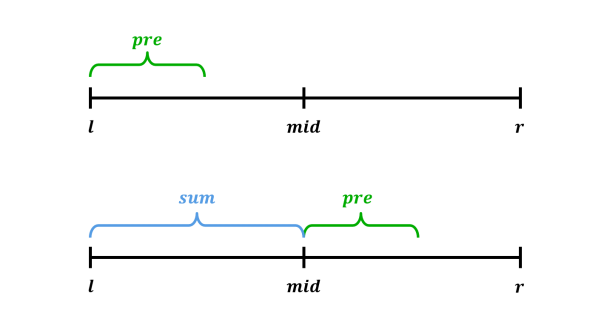
suf : Hậu tố lớn nhất của nút cha sẽ bằng max hậu tố của nút con bên phải và tổng giá trị của nút con bên phải cộng với hậu tố của nút con bên trái. Cách tính hậu tố tương tự như với tiền tố nên sẽ không minh họa lại nữa.
sum : Ta có thể dễ dàng tính toán giống như ở Ví dụ 1 bằng cách lấy tổng giá trị $2$ nút con.
maxsum :
- Xét $3$ trường hợp:
  - TH1: Đoạn con có tổng lớn nhất nằm hoàn toàn bên trong nút con bên trái.
  - TH2: Đoạn con có tổng lớn nhất nằm hoàn toàn bên trong nút con bên phải.
  - TH3: Một phần của đoạn con có tổng lớn nhất nằm ở nút con bên phải, và phần còn lại nằm ở nút con bên trái.
- Ở $2$ trường hợp đầu tiên thì ta chỉ cần trực tiếp lấy giá trị của đoạn con lớn nhất từ các nút con.
- Ở trường hợp thứ $3$, giá trị của đoạn con lớn nhất sẽ là tổng hậu tố lớn nhất của nút con bên trái với tiền tố lớn nhất của nút con bên phải.
  - Minh họa: Trường hợp $3$, với $mid = \big\lfloor \frac{l + r}{2} \big\rfloor$ :
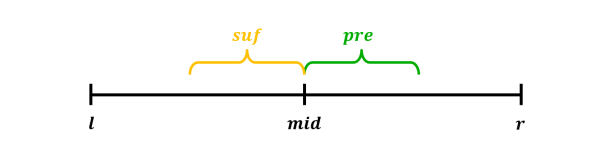
- Khi đó, giá trị của đoạn con lớn nhất nằm trong đoạn được quản lí bởi nút cha sẽ là giá trị lớn nhất của cả ba trường hợp trên.

Với mỗi truy vấn, đáp án chính là $\mathrm{maxsum}[x, y]$.

Cài đặt

Cấu trúc dữ liệu:

Hằng số inf = 1000000007.
Hằng số maxN = 50007.
Mảng st[] - Lưu thông tin của mỗi nút trên Segment Tree.

#include <bits/stdc++.h>

using namespace std;

const int inf  = 1e9 + 7;
const int maxN = 5e4 + 7;

// Thông tin của mỗi nút
struct node {
    int pre, suf, sum, maxsum;  

    static node base() { return { -inf, -inf, 0, -inf }; }

    // Hàm hợp nhất 2 nút con
    static node merge(const node& a, const node& b)  {
        node res;
        res.pre = max(a.pre, b.pre + a.sum);
        res.suf = max(b.suf, a.suf + b.sum);
        res.sum = a.sum + b.sum;
        res.maxsum = max(a.maxsum, b.maxsum);
        res.maxsum = max(res.maxsum, a.suf + b.pre);
        return res;
    }
};

int n, m;
int a[maxN];
node st[4 * maxN];

// Thủ tục xây dựng cây phân đoạn
void build(int id, int l ,int r) {
    if (l == r) {
        st[id] = { a[l], a[l], a[l], a[l] };
        return;
    }
    int mid = l + r >> 1;
    build(2 * id, l, mid);
    build(2 * id + 1, mid + 1, r);
    st[id] = node::merge(st[2 * id], st[2 * id + 1]);
}

// Hàm lấy giá trị
node get(int id, int l, int r, int u, int v){
    if (l >  v || r <  u) return node::base();
    if (l >= u && r <= v) return st[id];

    int mid = l + r >> 1;
    node g1 = get(2 * id, l, mid, u, v);
    node g2 = get(2 * id + 1, mid + 1, r, u, v);
    return node::merge(g1, g2);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);

    cin >> m;
    while (m--) {
        int x, y;
        cin >> x >> y;
        cout << get(1, 1, n, x, y).maxsum << '\n';
    }
}

Đánh giá

Độ phức tạp

Để xây dựng cây phân đoạn, ta mất độ phức tạp $\mathcal{O}(4 \times n)$. Với mỗi truy vấn, ta mất thêm độ phức tạp $\mathcal{O}(\log{n})$ cho mỗi thao tác lấy giá trị trên Segment Tree.

Nhìn chung, độ phức tạp của thuật toán là $\mathcal{O}(4 \times n + m \times \log{n})$.

Ví dụ 3

VNOI - ITDS1

Bài toán

Cho một dãy số có $N$ số. Bạn cần xử lí $2$ loại truy vấn:

Truy vấn loại $1$ có dạng $1 \space i \space v$, ta đổi số ở vị trí $i$ thành $v$.
Truy vấn loại $2$ có dạng $2 \space L \space R \space k$, ta cần in ra số nhỏ nhất mà lớn hơn bằng $k$ trong khoảng $[L..R]$.

$\circ \space \space 1 \le N, M \le 10^5$ (với $M$ là số lượng truy vấn).

Phân tích

Trong bài toán này, mỗi nút của cây phân đoạn là một multiset chứa các phần tử trong đoạn mà nó quản lí. Khi đó, để hợp nhất các nút con, ta chỉ cần insert toàn bộ phần tử của cả $2$ nút con vào nút cha.

Mỗi khi cập nhật cây phân đoạn, nếu ta duyệt từng phần tử của các nút con để insert vào nút cha thì với số lượng truy vấn $M$, ta sẽ mất độ phức tạp lên tới hơn $\mathcal{O}(M \times N)$ (chưa kể độ phức tạp của các thao tác trên multiset), vì số lượng phần tử của mỗi nút có thể lên tới $N$.

Thay vào đó, ta nhận thấy rằng, khi thay đổi giá trị $a[i]$ thành $v$ thì tất cả multiset của các nút quản lí phân đoạn chứa phần tử $a[i]$ (các nút nằm trên đường đi đơn từ gốc đến nút lá tương ứng) đều sẽ phải xóa đi một giá trị $a[i]$ và thêm vào một giá trị $v$. Do đó, với truy vấn loại $1$, khi cập nhật một nút, ta không cần phải insert lại toàn bộ phần tử của cả $2$ nút con, mà chỉ cần xóa đi một giá trị cũ trong multiset và chèn thêm giá trị mới.

Với truy vấn loại $2$, ta thực hiện tương tự như thao tác lấy giá trị. Tuy nhiên, mỗi khi xét đến nút mà đoạn nó quản lí nằm hoàn toàn bên trong đoạn cần truy vấn (trường hợp cơ sở), ta sử dụng hàm $\textit{lower_bound()}$ để trả ra giá trị nhỏ nhất mà vẫn lớn hơn hoặc bằng $k$ trong multiset của nút đó.

Cài đặt

Cấu trúc dữ liệu:

Hằng số inf = 1000000007.
Hằng số maxN = 100007.
Mảng st[] - Lưu thông tin của mỗi nút trên Segment Tree.

#include <bits/stdc++.h>
 
using namespace std;
 
const int inf  = 1e9 + 7;
const int maxN = 1e5 + 7;
 
int n, m;
int a[maxN];
multiset <int> st[4 * maxN];
 
void build(int id, int l, int r) {
    if (l == r) {
        st[id].insert(a[l]);
        return;
    }
    int mid = l + r >> 1;
    build(2 * id, l, mid);
    build(2 * id + 1, mid + 1, r);
    
    st[id] = st[2 * id + 1];
    for (auto x : st[2 * id]) st[id].insert(x);
}

void update(int id, int l, int r, int i, int old, int val) {
    if (l > i || r < i) return;
    if (l == r) {
        st[id].clear();
        st[id].insert(val);
        return;
    }
    int mid = l + r >> 1;
    update(2 * id, l, mid, i, old, val);
    update(2 * id + 1, mid + 1, r, i, old, val);
    st[id].erase(st[id].find(old));
    st[id].insert(val);
}

int get(int id, int l, int r, int u, int v, int k) {
    if (l >  v || r <  u) return inf; 
    if (l >= u && r <= v) {
        auto it = st[id].lower_bound(k);
        if (it == st[id].end()) return inf;
        return *it;
    }

    int mid = l + r >> 1;
    int get1 = get(2 * id, l, mid, u, v, k);
    int get2 = get(2 * id + 1, mid + 1, r, u, v, k);
    return min(get1, get2);
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);

    while (m--){
        int type, l, r, k;
        cin >> type;
        if (type == 1) {
            cin >> l >> k;
            update(1, 1, n, l, a[l], k);
            a[l] = k;
        }
        else {
            cin >> l >> r >> k;
            int ans = get(1, 1, n, l, r, k);
            cout << ((ans == inf) ? -1 : ans) << '\n';
        }
    }
}

Đánh giá

Ngoài ra còn có cách cài đặt khác đơn giản hơn, ta có thể cài đặt hàm update theo cách cập nhật "từ dưới lên trên" (không sử dụng đệ quy) như sau:

Ta sẽ bắt đầu xuất phát từ nút lá tương ứng với phần tử cần sửa đổi và đi dần lên nút gốc.

void update(int i, int val){
    /* leaf[i] là chỉ số của nút lá tương ứng với 
    phần tử ở vị trí i trong dãy số */
    int id = leaf[i]; 
    
    int old = *st[id].begin();
    while (id) {
        st[id].erase(st[id].find(old));
        st[id].insert(val);
        id /= 2;
    }
}

Tham khảo code chuẩn tại đây.

Độ phức tạp

Với thao tác xây dựng cây phân đoạn, ta thấy rằng, ở mỗi độ sâu của cây, ta sẽ phải duyệt hết toàn bộ phần tử trong dãy để insert vào multiset của các nút cha.

Ví dụ: Xét trường hợp tổng quát, với $N = 8$ là lũy thừa của $2$, ta có cây phân đoạn đầy đủ sau:
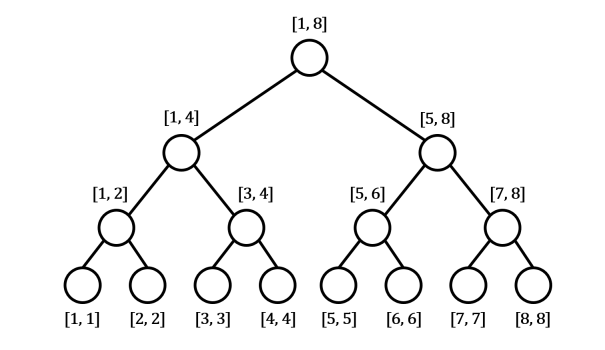
- Ở độ sâu thứ $4$, mỗi nút là nút lá của cây nên ta có thể lấy trực tiếp giá trị từ các phần tử tương ứng trong dãy số. Vì có $N$ nút lá nên ta sẽ mất độ phức tạp $\mathcal{O}(N)$.
- Ở độ sâu thứ $3$, để cập nhật giá trị cho nút quản lí đoạn $[1, 2]$ ta sẽ phải duyệt tất cả các phần tử của cả hai nút con, nghĩa là ta sẽ phải duyệt hết các phần tử trong đoạn $[1, 1]$ và $[2, 2]$. Tương tự với các nút quản lí đoạn $[3, 4]$, $[5, 6]$, $[7, 8]$. Do đó, ta cũng sẽ mất thêm độ phức tạp $\mathcal{O}(N)$.
- Ở độ sâu thứ $2$, để cập nhật giá trị cho nút quản lí đoạn $[1, 4]$ ta sẽ phải duyệt tất cả các phần tử của cả hai nút con, nghĩa là ta sẽ phải duyệt hết các phần tử trong đoạn $[1, 2]$ và $[3, 4]$. Tương tự với nút quản lí đoạn $[5, 8]$. Do đó, ta cũng sẽ mất thêm độ phức tạp $\mathcal{O}(N)$.
- Nhận thấy rằng, với mỗi độ sâu của cây, ta đều phải duyệt lại toàn bộ phần tử trong dãy nên sẽ mất độ phức tạp $\mathcal{O}(N)$.

Mà chiều cao của cây là $\mathcal{O}(\log{N})$ nên thao tác xây dựng cây phân đoạn có độ phức tạp là $\mathcal{O}(N \times \log^2{N})$ (độ phức tạp thời gian cho việc chèn, xóa và truy xuất thông tin trên multiset là $\mathcal{O}(\log{N})$).

Với mỗi thao tác cập nhật hoặc lấy giá trị, ta mất độ phức tạp $\mathcal{O}(\log^2{N})$.

Nhìn chung, độ phức tạp của thuật toán là $\mathcal{O}(N \times \log^2{N} + M \times \log^2{N})$.

Cập nhật lười (Lazy Propagation)

Đây là kĩ thuật được sử dụng trong Segment Tree để giảm độ phức tạp của Segment Tree với các truy vấn cập nhật đoạn.

Ý tưởng

Giả sử ta cần cập nhật đoạn $[u, v]$. Dễ thấy rằng, việc cập nhật tất cả các nút trên Segment Tree sẽ mất độ phức tạp rất lớn là $\mathcal{O}(N \times \log{N})$ (do tổng số phần tử nằm trong đoạn $[u, v]$ có thể lên đến $O(N)$). Do đó, với số lượng truy vấn cập nhật đoạn lớn, thao tác này sẽ không đủ tốt.

Vậy nên, trong quá trình cập nhật, ta chỉ thay đổi giá trị ở các nút gần gốc nhất sao cho tổng tất cả các phạm vi mà các nút đó quản lí đúng bằng đoạn $[u, v]$.

Ví dụ: Cho mảng $A = \{9,2,6,3,1,5,7\}$ và ta cần cập nhật đoạn $[1, 6]$ :
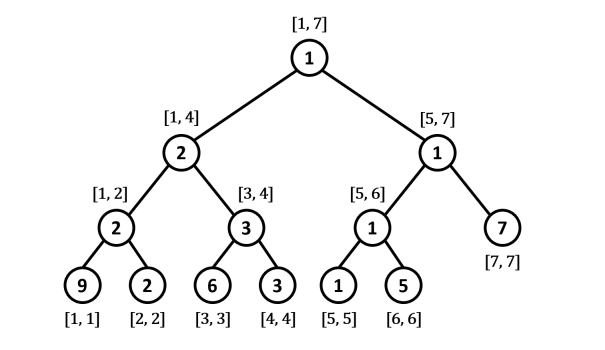
- Ta chỉ cập nhật giá trị ở các nút quản lý đoạn $[1, 4]$ và $[5, 6]$. Giá trị của các nút quản lý đoạn $[1, 2]$, $[3, 4]$, $[1, 1]$, $[2, 2]$, $[3, 3]$, $[4, 4]$, $[5, 5]$, $[6, 6]$ sẽ không đúng. Ta sẽ chỉ cập nhật lại giá trị của các nút này khi thật sự cần thiết (Do đó kĩ thuật này được gọi là lazy - lười biếng).

Cụ thể, ta xem xét bài toán sau:

Bài toán

VNOI - ITLAZY

Bạn được cho một mảng gồm $n$ số nguyên $a_1, a_2, …, a_n$ $(|a_i| \le 10^9,$ với $1 \le i \le n)$. Nhiệm vụ của bạn là xử lí $2$ loại truy vấn:

Loại $1$ có dạng $1 \space x \space y \space val$ : Tăng giá trị của các phần tử từ vị trí thứ $x$ đến vị trí thứ $y$ trong dãy lên $val$ đơn vị $(1 \le x \le y \le n, 1 \le val \le 10^9)$.
Loại $2$ có dạng $2 \space l \space r$ : In ra phần tử lớn nhất của dãy từ phần tử thứ $l$ đến phần tử thứ $r$ $(1 \le l \le r \le n)$.

Với mỗi truy vấn loại $2$, hãy in ra câu trả lời trên một dòng.

$\circ \space \space 1 \le n, q \le 10^5$ (với $q$ là số lượng truy vấn).

Phân tích

Ban đầu, ta thực hiện thủ tục xây dựng cây phân đoạn như bình thường.

Truy vấn loại $2$ là thao tác lấy giá trị cơ bản trên Segment Tree đã được phân tích trước đó.

Với truy vấn loại $1$, thao tác cập nhật đoạn $[u, v]$. Giả sử ta gọi $f[id]$ là giá trị lớn nhất trong đoạn mà nút $id$ quản lý. Trong lúc cập nhật, muốn hàm này thực hiện với độ phức tạp không quá $O(\log{N})$, thì khi xét đến $1$ nút $id$ quản lý đoạn $[l, r]$ mà đoạn $[l, r]$ nằm hoàn toàn trong đoạn $[u, v]$, thì ta không được đệ quy vào các nút con của nó nữa (nếu không độ phức tạp sẽ là $O(N)$ do ta đi vào tất cả các nút nằm trong đoạn $[u, v]$).

Để giải quyết, ta dùng kĩ thuật Lazy Propagation như sau:

Mỗi nút của Segment Tree sẽ lưu thêm một giá trị $lazy[id]$ với ý nghĩa là tất cả các phần tử trong đoạn $[l, r]$ mà nút $id$ quản lý đều được tăng thêm $lazy[id]$. Nói cách khác, nó sẽ lưu trữ các giá trị cần cập nhật của mỗi nút.
Ban đầu, ta khởi tạo tất cả các phần tử của mảng $lazy[]$ bằng $0$. Nếu $lazy[id] = 0$ có nghĩa là không có cập nhật nào đang chờ được xử lý trên nút $id$ trong cây phân đoạn. Ngược lại, nếu $lazy[id] \neq 0$ nghĩa là ta cần cập nhật giá trị của nút $id$ theo $lazy[id]$ trước khi thực hiện bất kỳ thao tác nào với nút đó (việc cập nhật này tùy vào mục đích của cây; ví dụ như trong bài toán trên, giá trị của nút $id$ sẽ được tăng thêm $lazy[id]$ ).
Nếu nút $id$ đang xét còn có giá trị được thêm vào chưa xét đến (từ các truy vấn cập nhật xảy ra trước đó, mà chưa được cập nhật hết), ta buộc phải cập nhật nó trước khi lấy giá trị hoặc tiếp tục đệ quy sâu hơn. Sau khi cập nhật xong nút $id$, ta phải đẩy giá trị $lazy$ ở nút $id$ xuống các con của nó để tiếp tục cập nhật và đặt lại $lazy$ của nút $id$ về $0$.
Để làm được điều này, ở đầu các hàm get và update ta thực hiện các thao tác sau:
- st[id] += lazy[id] - cập nhật giá trị nút $id$ theo $lazy[id]$.
- Nếu nút $id$ không phải là nút lá thì ta đẩy giá trị $lazy$ xuống các con của nó :
  - lazy[2 * id] += lazy[id]
  - lazy[2 * id + 1] += lazy[id]
- lazy[id] = 0 - chú ý ta cần phải thực hiện thao tác này, nếu không mỗi phần tử của dãy sẽ bị tăng lên nhiều lần, do ta đẩy xuống nhiều lần.
Bây giờ, để cập nhật đoạn, ta thực hiện tương tự như ở thao tác lấy giá trị, là xác định tập hợp ít nút nhất sao cho tổng tất cả các phạm vi mà các nút đó quản lí đúng bằng đoạn cần cập nhật. Khi đó, ta sửa lại giá trị của các nút thuộc tập hợp này và lưu lại giá trị cần cập nhật vào $lazy$ tương ứng với các nút con của chúng.

Cài đặt

Cấu trúc dữ liệu:

Hằng số inf = 1000000007.
Hằng số maxN = 100007.
Mảng st[] - Lưu thông tin của mỗi nút trên Segment Tree.
Mảng lazy[] - Lưu trữ các giá trị cần cập nhật của mỗi nút trên Segment Tree.

#include <bits/stdc++.h>

using namespace std;

const int inf  = 1e9 + 7;
const int maxN = 1e5 + 7;

int n, q;
int a[maxN];
long long st[4 * maxN], lazy[4 * maxN];

void build(int id, int l, int r) {
    if (l == r) {
        st[id] = a[l];
        return;
    }
    int mid = l + r >> 1;
    build(2 * id, l, mid);
    build(2 * id + 1, mid + 1, r);
    st[id] = max(st[2 * id], st[2 * id + 1]);
}

// Cập nhật nút đang xét và đẩy giá trị lazy xuống các nút con
void fix(int id, int l, int r) {
    if (!lazy[id]) return;
    st[id] += lazy[id];
    
    // Nếu id không phải là nút lá thì đẩy giá trị xuống các nút con
    if (l != r){
        lazy[2 * id] += lazy[id];
        lazy[2 * id + 1] += lazy[id];
    }
    
    lazy[id] = 0;
}

void update(int id, int l, int r, int u, int v, int val) {
    fix(id, l, r);
    if (l >  v || r <  u) return;
    if (l >= u && r <= v) {
        /* Khi cài đặt, ta LUÔN ĐẢM BẢO giá trị của nút được cập nhật ĐỒNG THỜI với
        giá trị Lazy Propagation. Như vậy sẽ tránh sai sót. */
        lazy[id] += val;
        fix(id, l, r);
        return;
    }
    int mid = l + r >> 1;
    update(2 * id, l, mid, u, v, val);
    update(2 * id + 1, mid + 1, r, u, v, val);
    st[id] = max(st[2 * id], st[2 * id + 1]);
}

long long get(int id, int l, int r, int u, int v) {
    fix(id, l, r);
    if (l >  v || r <  u) return -inf;
    if (l >= u && r <= v) return st[id];

    int mid  = l + r >> 1;
    long long get1 = get(2 * id, l, mid, u, v);
    long long get2 = get(2 * id + 1, mid + 1, r, u, v);
    return max(get1, get2);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);
    
    cin >> q;
    while (q--){
        int type, l, r, val;
        cin >> type >> l >> r;
        if (type == 1) {
            cin >> val;
            update(1, 1, n, l, r, val);
        }
        else cout << get(1, 1, n, l, r) << '\n';
    }
}

Đánh giá

Độ phức tạp

Tương tự như thao tác lấy giá trị, độ phức tạp của thao tác Lazy Propagation là $\mathcal{O}(\log{n})$.

Nhìn chung, độ phức tạp của cả bài toán là $\mathcal{O}(q \times \log{n})$.

Ví dụ 4

Codeforces - 558E A Simple Task

Bài toán

Cho một chuỗi kí tự $S$ độ dài $n$ (chỉ chứa các chữ cái tiếng Anh in thường) và $q$ truy vấn, mỗi truy vấn có dạng $i \space j \space k$ có nghĩa là hãy sắp xếp chuỗi con gồm các kí tự từ $i$ đến $j$ theo thứ tự không giảm nếu $k = 1$ hoặc theo thứ tự không tăng nếu $k = 0$.

In ra chuỗi cuối cùng sau khi đã thực hiện tất cả các truy vấn.

$1 \le n \le 10^5; \space 0 \le q \le 50000$.
$1 \le i \le j \le n; \space k \in { 0, 1 }$.

Phân tích

Để giải quyết bài toán, ta sử dụng kĩ thuật sắp xếp đếm phân phối (Counting sort). Vì vậy, đối với mỗi truy vấn, ta sẽ đếm số lần xuất hiện của mỗi ký tự và sau đó cập nhật đoạn như sau:

for (int x = i; x <= j; ++x) ++cnt[s[x] - 'a'];

int ind = (k ? 0 : 25);
for (int x = i; x <= j; ++x) {
    while (ind >= 0 && !cnt[ind]) ind += (k ? 1 : -1);
    s[x] = ind + 'a';
    --cnt[ind];
}

Tuy nhiên thuật toán trên không đủ tốt đối với số lượng truy vấn lớn. Do đó, ta cần một cấu trúc dữ liệu có thể hỗ trợ các hoạt động trên trong thời gian thích hợp.

Ta sẽ tạo ra $26$ mảng tương ứng với mỗi kí tự. Mảng này lưu lại vị trí xuất hiện của từng kí tự trong chuỗi. Và mỗi mảng sẽ được kiểm soát bởi một cây phân đoạn.

Ví dụ: Cho chuỗi $S = "dabedaba"$. Kí tự $'a'$ sẽ có một cây phân đoạn kiểm soát mảng $\{0, 1, 0, 0, 0, 1, 0, 1\}$. Còn kí tự $'b'$ có một cây phân đoạn kiểm soát mảng $\{0, 0, 1, 0, 0, 0, 1, 0\}$, v.v…

Với mỗi truy vấn sắp xếp đoạn $[i, j]$, ta dùng Segment Tree để tính số lần xuất hiện của mỗi ký tự trong đoạn, sau đó sắp xếp chúng và cập nhật mỗi cây phân đoạn với các giá trị mới.

Ví dụ: Cho chuỗi $S = "dabedaba"$, giả sử ta cần phải sắp xếp các kí tự của chuỗi $S$ theo thứ tự tăng dần:
- Gọi $cnt[i]$ là số lần xuất hiện của kí tự $i$ trong chuỗi $S$. Ta có thể dễ dàng tính toán mảng $cnt$ bằng cách lấy giá trị từ các cây phân đoạn tương ứng với mỗi kí tự.
- Sau khi lấy giá trị xong, trên cây phân đoạn, ta sẽ cập nhật lại tất cả phần tử của mảng tương ứng với từng kí tự bằng giá trị $0$.
- Tiếp theo, ta dùng cây phân đoạn để cập nhật mảng tương ứng với kí tự $'a'$ từ vị trí $1$ đến vị trí $3$ (do $cnt['a'] = 3$) bằng giá trị $1$ . Rồi lại tiếp tục cập nhật mảng tương ứng với kí tự $'b'$ từ vị trí $4$ đến vị trí $5$ (do $cnt['b'] = 2$) bằng giá trị $1$. Vì $cnt['c'] = 0$ nên ta bỏ qua kí tự $'c'$. Và lại tiếp tục với kí tự $'d'$, … đến kí tự $'z'$.
- Tương tự, để sắp xếp giảm dần, ta chỉ cần xét từ kí tự $'z'$ về kí tự $'a'$.

Ta sử dụng kỹ thuật Lazy Propagation để cập nhật các đoạn. Khác với ví dụ trên (ở mục Bài toán trong phần Cập nhật lười (Lazy Propagation)), khi cập nhật nút $id$ quản lí đoạn $[l, r]$ theo giá trị $lazy[id]$ thì giá trị của nút $id$ sẽ được tăng thêm $lazy[id] \times (r - l + 1)$. Vì đây là cây phân đoạn lấy tổng, nên khi mỗi phần tử tăng thêm $lazy[id]$ thì tổng giá trị của cả đoạn $[l, r]$ sẽ tăng thêm $lazy[id] \times (r - l + 1)$.

Vì thao tác cập nhật cây phân đoạn này là gán giá trị ($0$ hoặc $1$) nên ta sẽ khởi tạo giá trị ban đầu của mảng $lazy$ bằng $-1$.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 100007.
Mảng cnt[] - Lưu lại số lần xuất hiện của mỗi kí tự.
Mảng st[][] - Lưu thông tin của mỗi nút trên Segment Tree tương ứng với mỗi kí tự.
Mảng lazy[][] - Lưu trữ các giá trị cần cập nhật của mỗi nút trên Segment Tree tương ứng với mỗi kí tự.

#include <bits/stdc++.h>

using namespace std;

const int maxN = 1e5 + 7;

int n, q;
string s;
int cnt[30];
int st[30][4 * maxN], lazy[30][4 * maxN];

void build(int id, int l, int r) {
    // Khởi tạo giá trị mảng lazy ban đầu bằng -1
    for (int ch = 0; ch <= 25; ++ch) lazy[ch][id] = -1;

    if (l == r) {
        st[s[l - 1] - 'a'][id] = 1;
        return;
    }
    int mid = l + r >> 1;
    build(2 * id, l, mid);
    build(2 * id + 1, mid + 1, r);
    for (int ch = 0; ch <= 25; ++ch)
        st[ch][id] = st[ch][2 * id] + st[ch][2 * id + 1];
}

void fix(int id, int l, int r, int ch) {
    if (lazy[ch][id] == -1) return;
    st[ch][id] = lazy[ch][id] * (r - l + 1);
    if (l != r){
        
        /* Vì là thao tác gán giá trị chứ KHÔNG phải là tăng thêm một lượng
        nên lazy của nút con sẽ gán bằng lazy của nút cha */
        lazy[ch][2 * id] = lazy[ch][id]; 
        lazy[ch][2 * id + 1] = lazy[ch][id];
    }
    lazy[ch][id] = -1;
}

void update(int id, int l, int r, int u, int v, int val, int ch) {
    fix(id, l, r, ch);
    if (l >  v || r <  u) return;
    if (l >= u && r <= v) {
        lazy[ch][id] = val;
        fix(id, l, r, ch);
        return;
    }
    int mid = l + r >> 1;
    update(2 * id, l, mid, u, v, val, ch);
    update(2 * id + 1, mid + 1, r, u, v, val, ch);
    st[ch][id] = st[ch][2 * id] + st[ch][2 * id + 1];
}

int get(int id, int l, int r, int u, int v, int ch) {
    fix(id, l, r, ch);
    if (l >  v || r <  u) return 0;
    if (l >= u && r <= v) return st[ch][id];

    int mid  = l + r >> 1;
    int get1 = get(2 * id, l, mid, u, v, ch);
    int get2 = get(2 * id + 1, mid + 1, r, u, v, ch);
    return get1 + get2;
}

int main() {
    cin >> n >> q;
    cin >> s;
    build(1, 1, n);

    while (q--) {
        int i, j, k;
        cin >> i >> j >> k;

        for (int ch = 0; ch <= 25; ++ch) {
            cnt[ch] = get(1, 1, n, i, j, ch);
            update(1, 1, n, i, j, 0, ch);
        }

        int ch = (k ? 0 : 25), l = i;
        while (0 <= ch && ch <= 25) {
            if (cnt[ch]) {
                update(1, 1, n, l, l + cnt[ch] - 1, 1, ch);
                l += cnt[ch];
            }
            ch += (k ? 1 : -1);
        }
    }

    // In ra đáp án
    for (int i = 1; i <= n; ++i)
        for (int ch = 0; ch <= 25; ++ch)
            if (get(1, 1, n, i, i, ch)) {
                cout << (char)(ch + 'a');
                break;
            }
}

Đánh giá

Độ phức tạp

Độ phức tạp của thuật toán là $\mathcal{O}(q \times 26 \times \log{n})$.

Ví dụ 5

VNOI - ITLADDER

Bài toán

Cho một dãy số có $N$ số, ban đầu tất cả bằng $0$. Bạn cần xử lí $2$ loại truy vấn:

Truy vấn loại $1$ có dạng $1 \space L \space R \space A \space B$, ta cộng thêm vào phần tử thứ $i$ thêm $(i − L)A + B$ đơn vị với mọi $L \le i \le R$.
Truy vấn loại $2$ có dạng $2 \space L \space R$, ta cần in ra tổng của các phần tử trong khoảng $[L..R]$, lấy dư cho $10^9 + 7$.

$\circ \space \space 1 \le N, M \le 10^5$ (với $M$ là số lượng truy vấn). Các số trong input đều lớn hơn hoặc bằng $1$ và nhỏ hơn hoặc bằng $10^9$.

Phân tích

Với truy vấn loại $1$: Ta để ý đến giá trị được cộng vào. Với mọi $L \le i \le R$, ta cộng thêm vào phần tử thứ $i$ thêm $(i − L)A + B = iA + B - LA$ đơn vị. Trong đó $B – LA$ là không đổi với mọi phần tử trong truy vấn đề cập đến nên ta có thể dễ dàng sử dụng kĩ thuật Lazy Propagation để cập nhật. Còn lại là $iA$ đơn vị, giá trị này thay đổi nên phải dùng mảng $lazy$ thứ $2$ để lưu lại những giá trị dạng này. Nhận thấy rằng, khi mỗi phần tử trong đoạn $[l, r]$ tăng thêm $iA$ đơn vị thì tổng giá trị của cả đoạn $[l, r]$ sẽ tăng thêm $A \times (r + l) \times (r - l + 1) \space / \space 2$. Từ đó, bài toán chuyển về Segment Tree bình thường với $2$ mảng $lazy$.
Với truy vấn loại $2$ : Ta thực hiện thao tác lấy giá trị trên cây phân đoạn.

Cài đặt

Cấu trúc dữ liệu:

Hằng số maxN = 100007.
Mảng st[] - Lưu thông tin của mỗi nút trên Segment Tree.
Mảng lazy[] - Lưu trữ các giá trị cần cập nhật của mỗi nút trên Segment Tree.

#include <bits/stdc++.h>

using namespace std;

const int mod  = 1e9 + 7;
const int maxN = 1e5 + 7;

int n, m;
int st[4 * maxN];
pair <int, int> lazy[4 * maxN];

void fix(int id, int l, int r) {
    int a = lazy[id].first;
    int b = lazy[id].second;
    st[id] += (1ll * a * (r + l) * (r - l + 1) / 2) % mod;
    st[id] %= mod;
    st[id] += (1ll * b * (r - l + 1)) % mod;
    st[id] %= mod;
    
    if (l != r) {
        lazy[2 * id].first  = (lazy[2 * id].first  + a) % mod;
        lazy[2 * id].second = (lazy[2 * id].second + b) % mod;
        lazy[2 * id + 1].first  = (lazy[2 * id + 1].first  + a) % mod;
        lazy[2 * id + 1].second = (lazy[2 * id + 1].second + b) % mod;
    }
    lazy[id] = {0, 0};
}

void update(int id, int l, int r, int u, int v, int a, int b) {
    fix(id, l, r);
    if (l >  v || r <  u) return;
    if (l >= u && r <= v) {
        lazy[id].first  = a;
        lazy[id].second = (1ll * b - 1ll * u * a + 1ll * mod * mod) % mod;
        fix(id, l, r);
        return;
    }
    int mid = l + r >> 1;
    update(2 * id, l, mid, u, v, a, b);
    update(2 * id + 1, mid + 1, r, u, v, a, b);
    st[id] = (st[2 * id] + st[2 * id + 1]) % mod;
}

int get(int id, int l, int r, int u, int v) {
    fix(id, l, r);
    if (l >  v || r <  u) return 0;
    if (l >= u && r <= v) return st[id];

    int mid  = l + r >> 1;
    int get1 = get(2 * id, l, mid, u, v);
    int get2 = get(2 * id + 1, mid + 1, r, u, v);
    return (get1 + get2) % mod;
}

int main() {
    cin >> n >> m;
    while (m--) {
        int type, l, r, a, b;
        cin >> type >> l >> r;
        if (type == 1) {
            cin >> a >> b;
            update(1, 1, n, l, r, a, b);
        }
        else cout << get(1, 1, n, l, r) << '\n';
    }
}

Đánh giá

Độ phức tạp

Độ phức tạp của thuật toán là $\mathcal{O}(M \times \log{N})$.

Cây Phân Đoạn (cơ bản)

Mở đầu

Ý tưởng

Cấu trúc

Các thao tác trên cây phân đoạn

Xây dựng

Cập nhật

Lấy giá trị

Cài đặt

Đánh giá

Phân tích độ phức tạp

Bộ nhớ

Thời gian

Thao tác xây dựng

Thao tác cập nhật

Thao tác lấy giá trị

Ví dụ 1

Bài toán

Phân tích

Cài đặt

Đánh giá

Ví dụ 2

Bài toán

Phân tích

Cài đặt

Đánh giá

Ví dụ 3

Bài toán

Phân tích

Cài đặt

Đánh giá

Cập nhật lười (Lazy Propagation)

Ý tưởng

Bài toán

Phân tích

Cài đặt

Đánh giá

Ví dụ 4

Bài toán

Phân tích

Cài đặt

Đánh giá

Ví dụ 5

Bài toán

Phân tích

Cài đặt

Đánh giá

Bài tập áp dụng