Nguời viết:

Ngô Nhật Quang - HUS High School for Gifted Students

Reviewer:

Trần Quang Lộc - ITMO University
Hoàng Xuân Nhật - VNUHCM-University of Science
Hồ Ngọc Vĩnh Phát - VNUHCM-University of Science

Table of Contents

Giới thiệu
Bài toán
Cấu trúc dữ liệu Disjoint Set Union
Một số ứng dụng của DSU
Một số kĩ thuật sử dụng tính chất của DSU
- Kĩ thuật gộp set (Small-to-Large Merging)
- Kĩ thuật DSU trên cây (Sack)
Tham khảo
Bài tập

Giới thiệu

Disjoint Set Union, hay DSU, là một cấu trúc dữ liệu hữu dụng và thường xuyên được sử dụng trong các kì thi CP. DSU, đúng như tên gọi của nó, là một cấu trúc dữ liệu có thể quản lí một cách hiệu quả một tập hợp của các tập hợp.

Bài toán

Cho một đồ thị có $n$ đỉnh, ban đầu không có cạnh nào. Chúng ta phải xử lí các truy vấn như sau:

Thêm một cạnh giữa đỉnh $x$ và đỉnh $y$ trong đồ thị.
In ra YES nếu như đỉnh $x$ và đỉnh $y$ nằm trong cùng một thành phần liên thông. In ra NO nếu ngược lại.

Một thành phần liên thông trong đồ thị là một đồ thị con trong đó giữa bất kì hai đỉnh nào đều có đường đi đến nhau, và không thể nhận thêm bất kì một đỉnh nào mà vẫn duy trì tính chất trên.

Cấu trúc dữ liệu Disjoint Set Union

Nếu ta coi mỗi đỉnh trong đồ thị là một phần tử và mỗi thành phần liên thông trong đồ thị là một tập hợp, truy vấn thứ nhất sẽ trở thành gộp hai tập hợp lần lượt chứa phần tử $x$ và $y$ thành một tập hợp mới và truy vấn thứ hai trở thành hỏi hai phần tử $x$ và $y$ có nằm trong cùng một tập hợp hay không.

Để giải bài toán này, ta sẽ xây dựng một cấu trúc dữ liệu có ba thao tác như sau:

make_set(v) - tạo ra một tập hợp mới chỉ chứa phần tử v.
union_sets(a, b) - gộp tập hợp chứa phần tử a và tập hợp chứa phần tử b thành một.
find_set(v) - cho biết đại diện của tập hợp có chứa phần tử v. Đại diện này sẽ là một phần tử của tập hợp đó và có thể thay đổi sau mỗi lần gọi thao tác union_sets. Ta có thể sử dụng đại diện đó để kiểm tra hai phần tử có nằm trong cùng một tập hợp hay không. a và b nằm trong cùng một tập hợp nếu như đại diện của hai tập chứa chúng là giống nhau và không nằm trong cùng một tập hợp nếu ngược lại.

Ta có thể xử lí các thao tác một cách hiệu quả này với các tập hợp được biểu diễn dưới dạng các cây, mỗi phần tử là một đỉnh và mỗi cây tương ứng với một tập hợp. Gốc của mỗi cây sẽ là đại diện của tập hợp đó.

Cấu trúc của cây được thể hiện qua ví dụ sau đây:

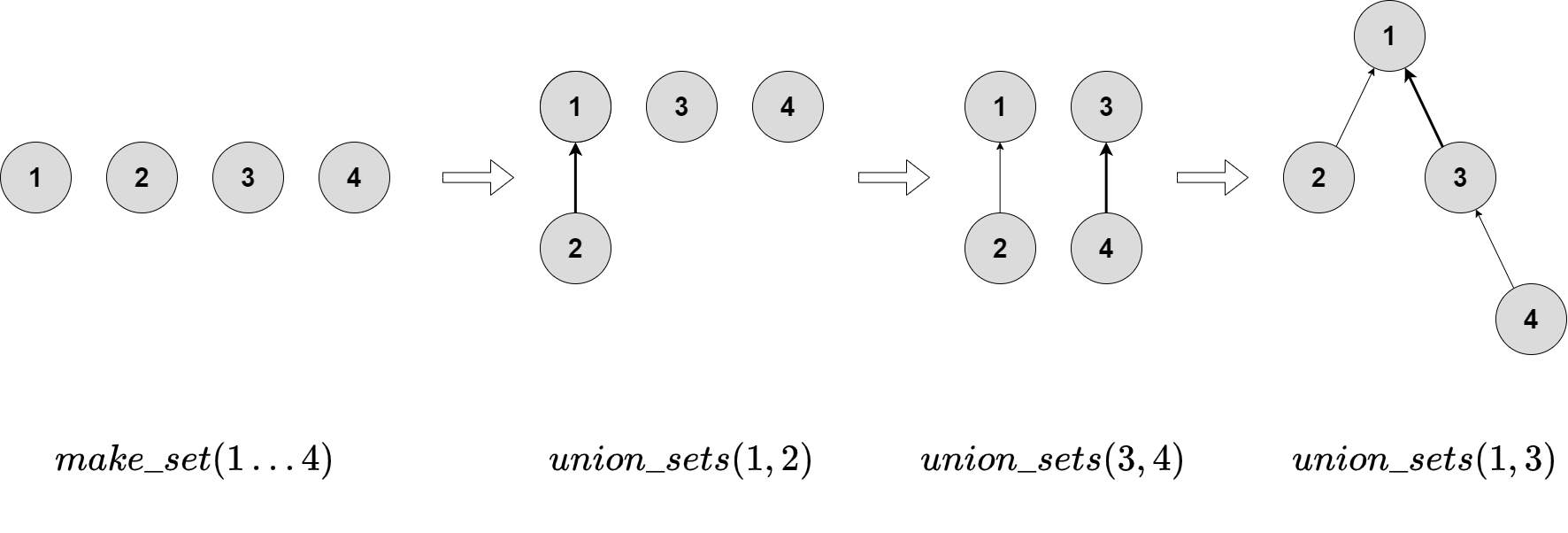
Ban đầu, mỗi phần tử thuộc một tập hợp riêng biệt, vậy mỗi đỉnh là một cây riêng biệt. Bước tiếp theo, ta gộp hai tập hợp chứa phần tử $1$ và $2$. Sau đó, ta gộp hai tập hợp chứa phần tử $3$ và $4$. Cuối cùng, ta gộp hai tập hợp chứa phần tử $1$ và $3$.

Với cách cài đặt này, ta sẽ lưu một mảng parent với parent[v] là cha của phần tử v.

Cài đặt "ngây thơ"

Để tạo một tập hợp mới gồm phần tử v (hay make_set(v)), ta chỉ cần tạo một cây có gốc là v, với parent[v] = v.

Để gộp hai tập hợp lần lượt chứa phần tử a và phần tử b (hay union_sets(a, b)), ta sẽ tìm gốc của cây có chứa phần tử a và gốc của cây có có chứa phần tử b. Nếu hai giá trị này giống nhau, ta sẽ không làm gì do hai phần tử này đã nằm trong cùng một tập hợp. Còn nếu không, ta sẽ đặt gốc cây này là cha của gốc cây còn lại. Dễ thấy điều này sẽ gộp hai cây lại thành một.

Để tìm kí hiệu của một tập hợp có chứa phần tử v (hay find_set(v)), ta đơn giản nhảy lên các tổ tiên của đỉnh v cho đến khi ta đến gốc của cây. Thao tác này có thể dễ dàng được cài đặt bằng đệ quy.

void make_set(int v) {
    parent[v] = v; // Tạo ra cây mới có gốc là đỉnh v
}

int find_set(int v) {
    if (v == parent[v]) return v; // Trả về đỉnh v nếu như đỉnh v là gốc của cây
    return find_set(parent[v]); // Đệ quy lên cha của đỉnh v
}

void union_sets(int a, int b) {
    a = find_set(a); // Tìm gốc của cây có chứa đỉnh a
    b = find_set(b); // Tìm gốc của cây có chứa đỉnh b
    if (a != b) parent[b] = a; // Gộp hai cây nếu như hai phần tử ở hai cây khác nhau
}

Như đã nói, đây là cách cài đặt ngây thơ, ta có thể dễ dàng tạo ra một ví dụ sao cho khi sử dụng cách cài đặt này, cây sẽ trở thành một đoạn thẳng gồm $n$ phần tử. Trong trường hợp này, độ phức tạp của thao tác find_set sẽ là $\mathcal{O}(n)$.

Điều này đương nhiên là không thể chấp nhận được, vì vậy ta sẽ tìm hiểu hai phương pháp tối ưu thuật toán dưới đây.

Tối ưu 1 - Gộp theo kích cỡ / độ cao

Phương pháp tối ưu này sẽ thay đổi thao tác union_sets. Chính xác hơn, ta sẽ thay đổi cách xét trong hai cây đang gộp, gốc của cây nào sẽ là cha của gốc của cây còn lại.

Có khá nhiều cách để xét điều này, nhưng hai cách được sử dụng nhiều nhất chính là gộp theo kích cỡ và gộp theo độ cao của cây.

Giả dụ mỗi cây có một giá trị. Ở cách thứ nhất, giá trị đó là kích cỡ của cây, và ở cách thứ hai, giá trị đó là độ cao của cây. Ở cả hai cách này, ta sẽ luôn đặt gốc của cây có giá trị cao hơn là cha của gốc của cây có giá trị thấp hơn.

Thao tác union_sets được tối ưu gộp theo kích cỡ:

void make_set(int v) {
    parent[v] = v;
    sz[v] = 1; // Ban đầu tập hợp chứa v có kích cỡ là 1
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    if (a != b) {
        if (sz[a] < sz[b]) swap(a, b); // Đặt biến a là gốc của cây có kích cỡ lớn hơn
        parent[b] = a;
        sz[a] += sz[b]; // Cập nhật kích cỡ của cây mới gộp lại
    } 
}

Thao tác union_sets được tối ưu gộp theo độ cao:

void make_set(int v) {
    parent[v] = v;
    rank[v] = 0; // Gốc của cây có độ cao là 0
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    if (a != b) {
        if (rank[a] < rank[b]) swap(a, b); // Đặt biến a là gốc của cây có độ cao lớn hơn
        parent[b] = a;
        if (rank[a] == rank[b]) rank[a]++; // Nếu như hai cây có cùng một độ cao, độ cao của cây mới sau khi gộp sẽ tăng 1
    } 
}

Chỉ cần sử dụng phương pháp tối ưu này, độ phức tạp của thao tác find_set sẽ trở thành $\mathcal{O}(\log{n})$. Tuy nhiên, ta vẫn còn có thể làm tốt hơn thế khi kết hợp với phương pháp tối ưu thứ hai.

Tối ưu 2 - Nén đường đi

Phương pháp tối ưu này nhằm tăng tốc thao tác find_set.

Giả dụ ta gọi find_set(v) với một đỉnh v bất kì, chúng ta tìm được p là gốc của cây, đồng thời cũng là giá trị của mọi hàm find_set(u) với u là một đỉnh nằm trên đường đi từ u đến p. Cách tối ưu ở đây chính là làm cho đường đi đến gốc của các đỉnh u ngắn đi bằng cách gán trực tiếp cha của các đỉnh u này thành p.

Có thể thấy sau khi thực hiện một thao tác như vậy, cấu trúc cả cây có thể thay đổi. Ta có thể thấy điều này trong ví dụ sau đây:

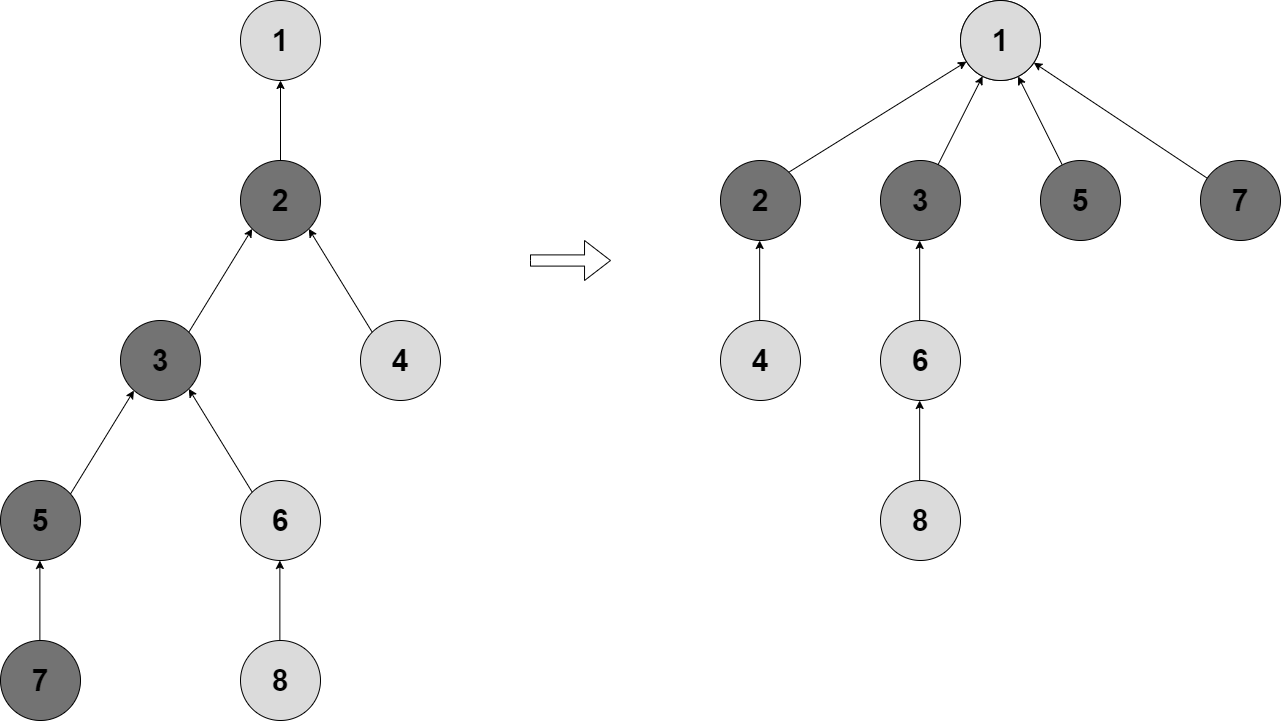
Bên trái là cây ban đầu và bên phải là cây bị nén sau khi ta sử dụng thao tác find_set(7), nén đường đi tới gốc của các đỉnh $7, 5, 3, 2$.

Thao tác find_set mới này được cài đặt như sau:

int find_set(int v) {
    if (v == parent[v]) return v; // Trả về đỉnh v nếu như đỉnh v là gốc của cây
    int p = find_set(parent[v]); // Đệ quy lên cha của đỉnh v
    parent[v] = p; // Nén đoạn từ v lên gốc của cây
    return p;
}

Một cách cài đặt khác của thao tác find_set mà thường được sử dụng nhiều trong CP do tính ngắn gọn của nó:

int find_set(int v) {
    return v == parent[v] ? v : parent[v] = find_set(parent[v]);
}

Độ phức tạp thời gian

Khi kết hợp cả hai phương pháp tối ưu bên trên lại, ta sẽ đạt được độ phức tạp trung bình cho thao tác find_set là $\mathcal{O}(\alpha(n))$ với $\alpha(n)$ là hàm Ackermann nghịch đảo. Tuy nhiên hàm này tăng rất chậm (với $\alpha(n) \le 3$ với $n \le 61$ và $\alpha(n) \le 4$ với xấp xỉ $n < 10^{600}$).

Độ phức tạp trung bình, đúng như tên gọi của nó, là tổng độ phức tạp của các thao tác, chia cho số lượng thao tác. Điều này có nghĩa ở một số thao tác, độ phức tạp có thể lên tới $\mathcal{O}(\log{n})$ nhưng ta thực hiện $m$ thao tác như vậy, độ phức tạp sẽ trở thành $\mathcal{O}(m \cdot \alpha(n))$ ($\approx \mathcal{O}(m)$ với $m$ đủ lớn).

Một điều đáng lưu ý là nếu như chúng ta chỉ sử dụng phương pháp tối ưu $2$, độ phức tạp trung bình của thao tác find_set cũng chỉ là $\mathcal{O}(\log{n})$.

Chứng minh độ phức tạp thời gian

Tối ưu gộp set theo kích cỡ: Gọi $a$ là độ lớn của cây con có gốc là đỉnh $v$, $b$ là độ lớn của cây con có gốc là $p$ (cha của đỉnh $v$). Dễ thấy rằng $b \ge 2 \times a$ do số lượng đỉnh trong cây con gốc $p$ mà không thuộc cây con gốc $v$ lớn hơn hoặc bằng $a$. Do vậy độ sâu tối đa của cây sẽ là $\log_2{n}$.

Tối ưu gộp set theo độ cao: Ta sẽ chứng minh một cây có độ cao là $k$ có ít nhất $2^k$ đỉnh. Có thể thấy rằng số cây có độ cao là $0$ có chính xác $1$ đỉnh. Một cây chỉ có thể có độ cao là $k$ nếu như trước đó độ cao của nó là $k - 1$ và nó được gộp với một cây khác có độ cao là $k - 1$. Vì vậy, số đỉnh trong cây có độ cao là $k$ sẽ lớn hơn hoặc bằng hai lần số đỉnh trong cây có độ cao là $k - 1$. Do đó độ cao lớn nhất có thể của cây sẽ là $\log_2{n}$.

Kết hợp hai phương pháp tối ưu: Phần chứng minh này khá dài dòng và khó hiểu, bạn đọc có thể tìm hiểu tại đây hoặc đây.

Một cách cài đặt khác

Ở trong một số tài liệu như Giải thuật và lập trình (thầy Lê Minh Hoàng) hay thư viện Atcoder, thay vì cài đặt cấu trúc dữ liệu DSU bằng hai mảng parent và sz, chỉ một mảng lab được sử dụng.

Nếu như lab[v] âm thì $u$ là gốc của một cây và -lab[v] là số lượng đỉnh của cây đó. Còn nếu lab[v] dương thì lab[v] là cha của đỉnh $u$.

void make_set(int v) {
    lab[u] = -1;
}

int find_set(int v) {
    return lab[v] < 0 ? v : lab[v] = find_set(lab[v]);
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    
    if (a != b) {
        if (lab[a] > lab[b]) swap(a, b);
        lab[a] += lab[b];
        lab[b] = a;
    }
}

Một số ứng dụng của DSU

Lưu thêm thông tin khác cho mỗi tập hợp

Ngoài việc lưu các thông tin về cấu trúc cây, ta có thể lưu các hàm có tính chất giao hoán và kết hợp của từng tập hợp. Ví dụ, ta có thể lưu tổng các phần tử/ giá trị phần tử bé nhất của từng tập hợp. Lúc này, các thao tác của dsu sẽ được cài đặt như sau:

void make_set(int v) {
    parent[v] = v;
    sz[v] = 1;
    mn[v] = value[v];
    sum[v] = value[v];
    // value[v] là giá trị của phần tử thứ v
}

int find_set(int v) {
    return v == parent[v] ? v : parent[v] = find_set(parent[v]);
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    if (a != b) {
        if (sz[a] < sz[b]) swap(a, b);
        parent[b] = a;
        sz[a] += sz[b];
        sum[a] += sum[b];
        mn[a] = min(mn[a], mn[b]);
    } 
}

Có thể thấy rằng, tương tự như thông tin về độ lớn của cây (sz) hay độ cao của cây (rank), ta sẽ lưu các hàm này tại gốc của từng cây.

int find_sum(int v) { // Trả về tổng của các phần tử trong tập hợp chứa v
    v = find_set(v);
    return sum[v];
}

int find_min(int v) { // Trả về giá trị bé nhất của các phần tử trong tập hợp chứa v
    v = find_set(v);
    return mn[v];
}

Bài toán xếp hàng

Bài toán

Cho $n$ người đang xếp hàng ở các vị trí từ $1$ đến $n$. Viết chương trình xử lí các truy vấn:

Người đứng ở vị trí thứ $i$ rời khỏi hàng.
Tìm người gần nhất về bên phải vị trí $p$ mà chưa rời khỏi hàng.

Lời giải

Với mỗi vị trí, ta sẽ có một con trỏ. Nếu người đứng ở vị trị này vẫn đang đứng trong hàng, con trỏ trỏ vào vị trị đó, nếu không thì con trỏ này sẽ trỏ vào vị trí ngay bên phải.

Xét ví dụ sau với $n = 5$, ban đầu ta có:

Giả dụ người đứng ở vị trí $2$ và $3$ rời khỏi hàng:

Dễ thấy để tìm người gần nhất bên phải mà chưa rời khỏi hàng, ta đi dần dần sang phải cho đến khi gặp một vị trí có con trỏ trỏ đến chính nó.

Chúng ta có thể sử dụng cấu trúc dữ liệu DSU để lưu trữ các thông tin trên và sử dụng phương pháp tối ưu nén đoạn để đạt được độ phức tạp trung bình $\mathcal{O}(\log{n})$ với mỗi truy vấn.

Để ý kĩ hơn, ta thấy vị trí ta cần tìm chính là vị trí có thứ tự lớn nhất trong tập hợp. Ta có thể lưu phần tử lớn nhất trong một tập hợp như đã nói ở phần trên, qua đó đạt được độ phức tạp trung bình $\mathcal{O}(\alpha{(n)})$ với mỗi truy vấn.

Code mẫu

void make_set(int v) {
    parent[v] = v;
    sz[v] = 1;
    mx[v] = v;
}

int find_set(int v) {
    return v == parent[v] ? v : parent[v] = find_set(parent[v]);
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    if (a != b) {
        if (sz[a] < sz[b]) swap(a, b);
        parent[b] = a;
        sz[a] += sz[b];
        mx[a] = max(mx[a], mx[b]);
    } 
}

void leave(int v) { // Người thứ v rời khỏi hàng
    union_sets(v, v + 1);
}

int find_next(int p) { // Trả vè thứ tự của người gần nhất về bên phải 
                       // vị trí p mà chưa rời khỏi hàng
    p = find_set(p);
    return mx[p];
}

Tối ưu thuật toán tìm cây khung nhỏ nhất trong đồ thị

Sử dụng DSU, ta có thể tối ưu độ phức tạp của thuật toán tìm cây khung nhỏ nhất của đồ thị từ $\mathcal{O}(m \log{n} + n^2)$ xuống $\mathcal{O}(m \log{n})$.

Bạn đọc có thể tìm hiểu kĩ hơn ở blog tìm cây khung nhỏ nhất trong đồ thị.

Đảo ngược truy vấn

Do tính chất một chiều của cấu trúc dữ liệu DSU (chỉ thêm chứ không xóa được), ở một số bài ta phải đảo ngược thứ tự của các truy vấn trong bài để giải.

Bài toán

Codeforces 722C - Destroying Array

Cho mảng gồm $n$ số nguyên không âm $a_1, a_2, \ldots, a_n$ và một hoán vị các số từ $1$ đến $n$.

Các phần tử sẽ lần lượt bị phá hủy theo thứ tự hoán vị trên. Sau mỗi lần một phần tử bị phá hủy, hãy in ra dãy con liên tiếp có tổng lớn nhất mà không có phần tử nào đã bị phá hủy. Tổng của một đoạn con rỗng là $0$.

Giới hạn: $1\le n \le 10^5, 0 \le a_i \le 10^9$.

Lời giải

Do các phần tử là các số nguyên không âm, ta có thể thấy rằng nếu sau khi một số phần tử bị phá hủy, dãy bị chia thành $k$ đoạn con liên tiếp thì đáp án sẽ là một trong $k$ đoạn con này.

Đảo ngược thứ tự của các truy vấn, ta có thể thấy bài toán trở nên dễ dàng rất nhiều: Hồi sinh một số bị phá hủy trở về ban đầu và in ra đoạn con có tổng lớn nhất. Đến đây ta nghĩ tới cấu trúc dữ liệu DSU để xử lí các đoạn con liên tiếp.

Khi một số được hồi sinh, ta sẽ kiểm tra bên trái số đó, nếu có số nào đã được hồi sinh từ trước thì ta sẽ thêm cạnh giữa số đó và số bên trái số đó. Tương tự với số bên phải. Dễ thấy rằng mọi lúc các thành phần liên thông trong DSU sẽ thể hiện cho một đoạn con liên tiếp. Việc lưu trữ tổng của một thành phần liên thông đã được nhắc đến ở phần trước.

Code mẫu

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 1e5 + 5;
int n, ans;
int a[N], p[N], res[N];
bool flag[N];

struct DSU{
    vector<int> parent, sz, sum;

    DSU(int n) : parent(n), sz(n), sum(n) {};

    void make_set(int v) {
        parent[v] = v;
        sz[v] = 1;
        sum[v] = a[v];
    }
     
    int find_set(int v) {
        return v == parent[v] ? v : parent[v] = find_set(parent[v]);
    }

    void join_sets(int a, int b) {
        a = find_set(a);
        b = find_set(b);
        if (a != b) {
            if (sz[a] < sz[b]) swap(a,b);
            parent[b] = a;
            sz[a] += sz[b];
            sum[a] += sum[b];
        }
    }
};

signed main() {
        
    ios_base::sync_with_stdio(false); cin.tie(NULL);

    cin >> n;
    
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> p[i];

    DSU g(n + 5);
    for (int i = 1; i <= n; i++) g.make_set(i);    
    for (int i = n; i >= 1; i--) {
        flag[p[i]] = true;

        if (p[i] > 1 && flag[p[i] - 1]) g.join_sets(p[i], p[i] - 1);
        if (p[i] < n && flag[p[i] + 1]) g.join_sets(p[i], p[i] + 1);

        ans = max(ans, g.sum[g.find_set(p[i])]);
        res[i - 1] = ans;
    }
        
    for (int i = 1; i <= n; i++) cout << res[i] << "\n";
        
}

Kiểm tra tính chất hai phía của đồ thị online

Bài toán

Cho một đồ thị có $n$ đỉnh, ban đầu không có cạnh nào. Xử lí các truy vấn thêm cạnh vào đồ thị. Hỏi sau truy vấn nào thì đồ thị không còn là đồ thị hai phía?

Lời giải

Dựa vào tính chất của đồ thị hai phía, dễ thấy rằng với mọi cặp đỉnh thuộc cùng một phía sẽ có đường đi bắt kì giữa chúng có độ dài chẵn. Nói cách khác, nếu ta chọn một đỉnh $l$ trong một thành phần liên thông, hai đỉnh $a$ và $b$ sẽ nằm cùng một phía nếu như khoảng cách của hai đỉnh này tới đỉnh $l$ có cùng tính chẵn lẻ.

Chúng ta hoàn toàn có thể sử dụng cấu trúc dữ liệu DSU để lưu trữ thông tin này bằng cách lưu tính chẵn lẻ của đường đi từ mọi đỉnh tới gốc của cây. Lúc này, hàm find_set của ta sẽ trả về một cặp {gốc của cây, tính chẵn lẻ của độ dài đường đi đến gốc của cây} và được cài đặt như sau:

pair<int, int> find_set(int v) {
    if (v == parent[v]) return {v, 0};
    pair<int, int> val = get(parent[v]);
    parent[v] = val.first;
    dist[v] = (dist[v] + val.second) % 2;
        // độ dài từ đỉnh đến cha mới 
        // = độ dài đến đỉnh cha cũ 
        // + độ dài từ cha cũ tới cha mới (gốc của cây)
    return {p[a], dist[a]};
}

Hàm union_sets, tương tự, cũng cần phải được thay đổi và được cài đặt như sau:

void union_sets(int a, int b) {
    pair<int, int> valA = find_set(a),
                   valB = find_set(b);
    a = valA.first; b = valB.first;
    
    if (a == b) {
        if (valA.second != valB.second) {
            // Đồ thị không còn là đồ thị hai phía do có
            // cạnh nối giữa hai đỉnh thuộc hai phía khác nhau.
        }
    }
    
    else {
        if (sz[a] < sz[b]) swap(a, b);
        parent[b] = a;
        sz[a] += sz[b];
        dist[b] = (valA.second + valB.second + 1) % 2;
            // Độ dài từ đỉnh b tới gốc cây
            // = Độ dài từ đỉnh a tới gốc cây ban đầu chứa a
            // + Dộ dài từ đỉnh b tới gốc cây ban đầu chứa b
            // + 1 (Khoảng cách giữa hai đỉnh a và b)
    } 
}

Một số kĩ thuật sử dụng tính chất của DSU

Ngoài ra tính chất của DSU còn được sử dụng trong một số kĩ thuật khá phổ biến.

Kĩ thuật gộp set (Small-to-Large Merging)

Giả sử ta cần lưu trực tiếp các phần tử của một tập hợp bằng một cấu trúc dữ liệu như set/map, thì liệu có cách nào đủ hiệu quả để thực hiện thao tác union_sets hay không? Câu trả lời là có và kĩ thuật này được gọi là gộp set (small-to-large merging).

Bài toán

VNOJ - colquery

Cho một đồ thị vô hướng có $n$ đỉnh, đỉnh thứ $i$ có màu $a_i$. Ban đầu đồ thị chưa có cạnh nào.

Cho $q$ truy vấn, mỗi truy vấn thuộc một trong hai dạng sau:

$1\,u\,v$: Thêm một cạnh nối giữa $u$ và $v$.
$2\,u\,c$: Tính số đỉnh có màu $c$ trong thành phần liên thông chứa $u$.

Lời giải

Chúng ta vẫn sẽ sử dụng cấu trúc dữ liệu DSU trong bài này, và lưu thêm một map chứa số lượng từng màu tại gốc của từng cây.

Trong thao tác union_sets, ta sẽ chuyển lần lượt các phần tử trong map của tập hợp bé hơn vào map của tập hợp lớn hơn. Thoạt nhìn ban đầu, việc làm này có độ phức tạp tổng là $\mathcal{O}(n ^ 2)$, nhưng thực chất nó chỉ là $\mathcal{O}(n \log{n})$. Ta sẽ chứng minh tại sao.

Gọi số phần tử nằm trong hai dãy số lớn hơn và bé hơn lần lượt là $a$ và $b$. Dễ thấy được rằng $a + b \ge 2 \cdot b$, nên mỗi lần một phần tử bị di chuyển, nó sẽ bị di chuyển tới một dãy số có kích thước lớn hơn ít nhất hai lần kích thước dãy số ban đầu nó nằm trong. Vì vậy mà ta thấy rằng một phần tử chỉ bị di chuyển tối đa $\log_2{n}$ lần, qua đó mà đạt được độ phức tạp $\mathcal{O}(n \log{n})$.

Code mẫu

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
int n, q;
int a[N];

struct DSU{
    vector<map<int, int>> color;
    vector<int> parent, sz;

    DSU(int n) : color(n), parent(n), sz(n) {};

    void make_set(int v) {
        color[v][a[v]] = 1;
        parent[v] = v;
        sz[v] = 1;
    }

    int find_set(int v) {
        if (v == parent[v]) return v;
        int p = find_set(parent[v]);
        parent[v] = p;
        return p;
    }

    void union_sets(int a, int b) {
        a = find_set(a);
        b = find_set(b);
        if (a != b) {
            if (sz[a] < sz[b]) swap(a, b);
            parent[b] = a;
            sz[a] += sz[b];

            for (auto p : color[b]) color[a][p.first] += p.second;
            color[b].clear();
        } 
    }

    int query(int v, int c) {
        v = find_set(v);
        return color[v].find(c) != color[v].end() ? color[v][c] : 0;
    }
};

signed main() {
    
    ios_base::sync_with_stdio(false); cin.tie(NULL);
    
    cin >> n >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];

    DSU g(n + 5);
    for (int i = 1; i <= n; i++) g.make_set(i);
    while (q--) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) g.union_sets(x, y);
        else cout << g.query(x, y) << "\n";
    }
}

Độ phức tạp thuật toán: $\mathcal{O}(n \log^2{n})$, có thêm một $\log$ do ta phải lưu giữ thông tin bằng cấu trúc dữ liệu map.

Kĩ thuật DSU trên cây (Sack)

Đây là một thuật toán sử dụng ý tưởng gộp set ở phần trước để giải quyết một số bài toán truy vấn trên cây một cách hiệu quả.

Bài toán

Cho một cây có $n$ đỉnh với gốc là đỉnh $1$, đỉnh thứ $i$ được tô màu $c_i$. Cho $q$ truy vấn có dạng $v\,c$, với mỗi truy vấn in ra số lượng đỉnh có màu $c$ trong cây con gốc $v$.

Lời giải

Sử dụng ý tưởng gộp set ở phần trước, ta có thể dễ dàng đạt được độ phức tạp $\mathcal{O}(n \log^2{n} + q\log{n})$. Tuy nhiên, ta còn có thể làm tốt hơn với kĩ thuật DSU trên cây

Bằng cách thay đổi cách dfs, ta có thể loại bỏ một $\log$ của cấu trúc dữ liệu map trong độ phức tạp, qua đó mà đạt được độ phức tạp $\mathcal{O}(n \log{n} + q)$. Ta sẽ tham khảo đoạn code dưới đây để hiểu hơn kĩ thuật này:

int sz[N];
int cnt[N];

void pre_dfs(int u, int p) { // Một hàm dfs chạy trước 
                             // để tính được độ lớn của từng cây con
    sz[u] = 1;
    for (auto v : g[u]) if (v != p) {
        pre_dfs(v, u);
        sz[u] += sz[v];
    }
}

void update(int u, int p, int delta) {
    cnt[color[u]] += delta;
    for (auto v : g[u]) if (v != p) update(v, u, delta);
} 

void dfs(int u, int p) {
    int bigChild = -1;
    for (auto v : g[u]) if (v != p) {
        if (bigChild == -1 || sz[v] > sz[bigChild]) bigChild = v;
    } // Tìm cây con lớn nhất trong 
      // các con trực tiếp của đỉnh u

    for (auto v : g[u]) if (v != p && v != bigChild) {
        dfs(v, u);
        update(v, u, -1);
    }
    if (bigChild != -1) dfs(bigChild, u);

    for (auto v : g[u]) if (v != p && v != bigChild) update(v, u, 1);
    cnt[color[u]]++;
    
    // Trả lời các truy vấn tại đỉnh u, với cnt[c] 
    // là số lượng đỉnh có màu c trong cây con gốc u
}

Với cây con gốc $u$ đang xét, ta sẽ dfs xuống giải bài toán với đỉnh $v$ là con trực tiếp của đỉnh $u$. Nếu giải như bài toán colquery, ở mỗi đỉnh ta sẽ lưu một cấu trúc dữ liệu map để lưu số lượng từng màu trong cây con đó. Sau đó ta sẽ gộp chúng lại để có được map chứa số lượng từng màu trong cây con gốc $u$ (Gộp các map của cây con không phải cây con lớn nhất vào map của cây con lớn nhất).

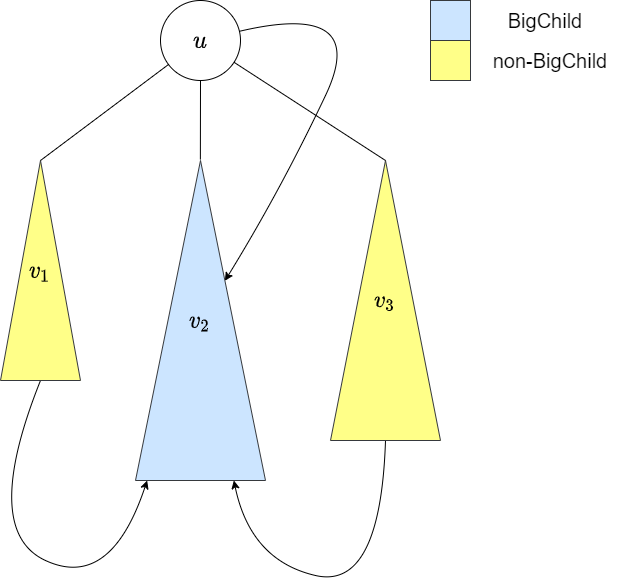
Tuy nhiên, sự tối ưu của kỹ thuật này chính là ta có thể đảo thứ tự dfs và trả lời các truy vấn offline.

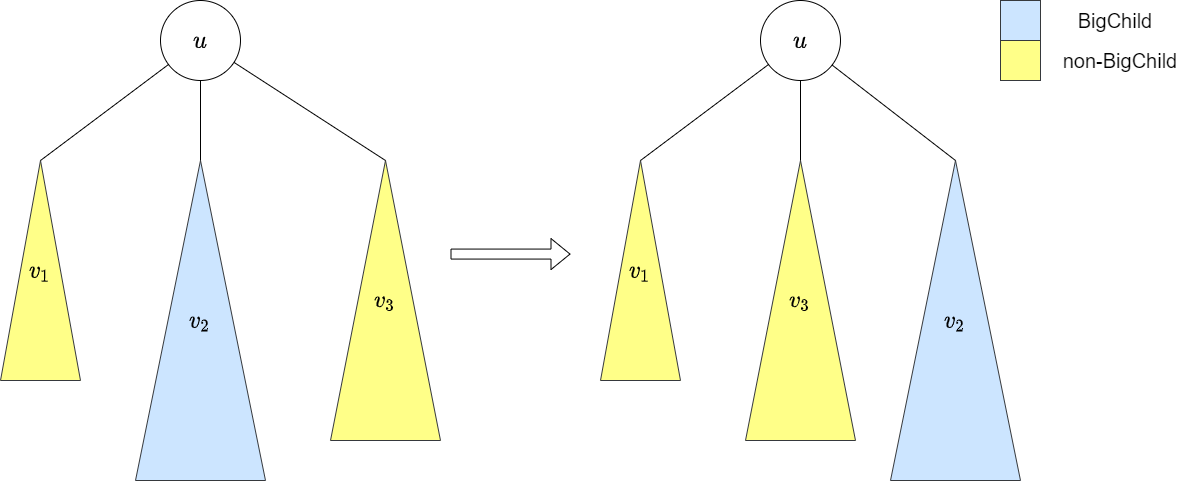
Ta sẽ sử dụng duy nhất một mảng để đếm số lượng từng màu trong một cây con. Bằng cách nào đó, đến cuối hàm dfs của cây con gốc $u$, ta có sẽ có mảng $cnt$ với $cnt[c]$ là số lượng đỉnh có màu $c$ trong cây con gốc $u$.

Do dùng chung một mảng chứ không phải lưu riêng từng cây con trong map riêng biệt, nên trước khi ta dfs xuống để giải bài toán cho các con tiếp theo, ta phải cập nhật "xóa" đi các màu của các cây con đã dfs từ trước khỏi mảng để tránh ghi đè lên đáp án. Do đó ta thấy chỉ có màu trong cây con được dfs cuối cùng là không nhất thiết phải xóa đi ngay lập tức.

Gọi đỉnh $v$ có cây con lớn nhất là bigChild. Với ý tưởng gộp màu trong các cây con khác vào cây con bigChild, hay nói cách khác ta không được phép di chuyển các màu trong cây con bigChild, ta sẽ đảo thứ tự dfs của bigChild xuống cuối cùng và giữ lại các màu trong mảng mà không xóa đi. Tiếp đó ta sẽ dfs xuống các cây không phải bigChild chỉ để thêm lại các màu vào mảng, qua đó mà tìm được số lượng từng màu trong cây con gốc $u$. Dễ thấy bằng cách này ta đã loại bỏ hoàn toàn việc sử dụng cấu trúc dữ liệu map, qua đó mà giảm được một $\log$ trong độ phức tạp thời gian.

Ta có thể thấy rõ hơn thông tin mà mảng $cnt$ lưu trữ trong quá trình sau đây:

Chú thích	Minh họa
dfs xuống cây con $v_1$, lúc này trong mảng $cnt$ chứa các màu trong cây con này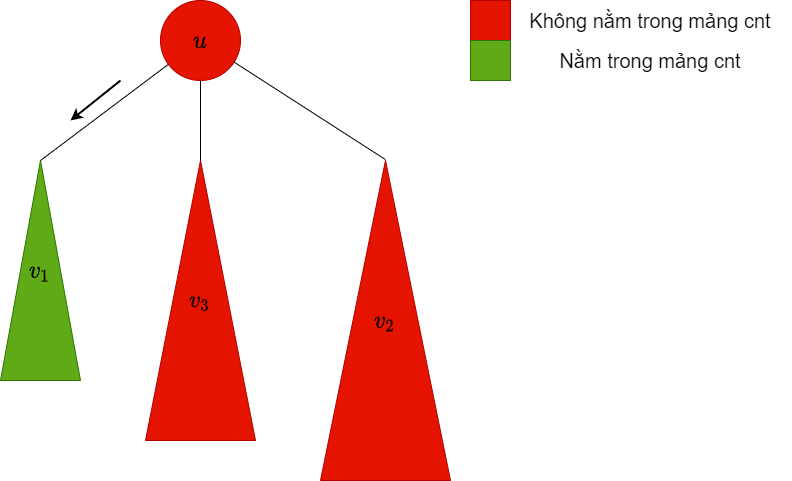
$v_1$ không phải `bigChild`, do đó ta xóa các màu trong cây con này ra khỏi mảng $cnt$
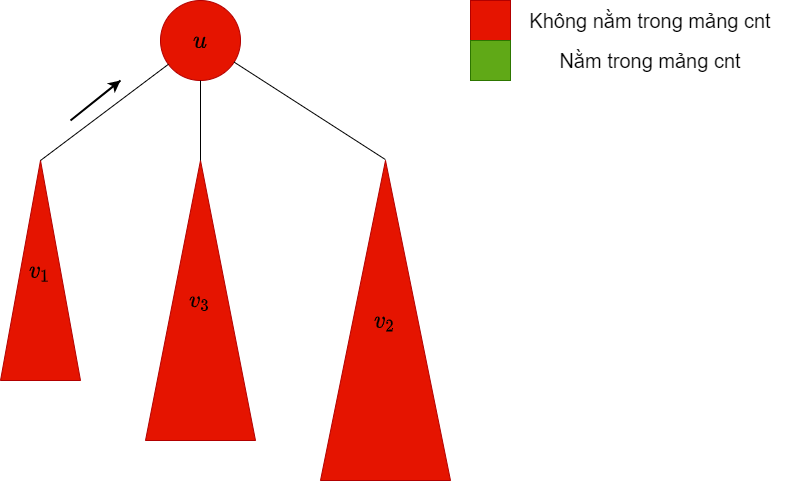dfs xuống cây con $v_3$, lúc này trong mảng $cnt$ chứa các màu trong cây con này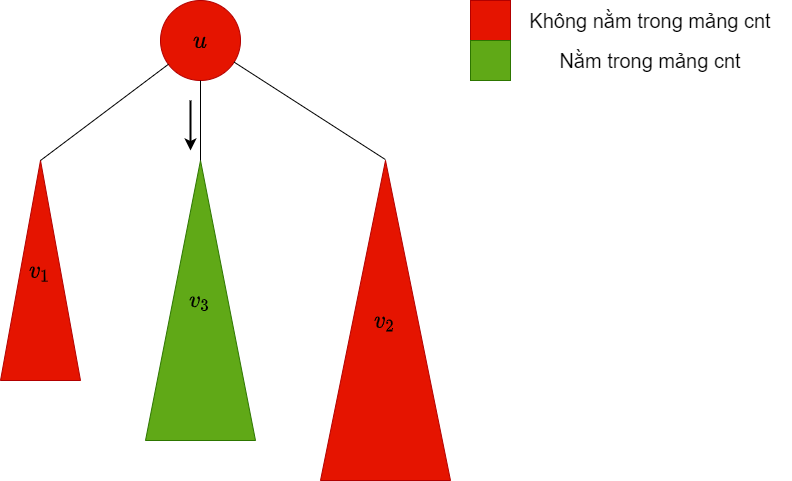
$v_3$ không phải `bigChild`, do đó ta xóa các màu trong cây con này ra khỏi mảng $cnt$
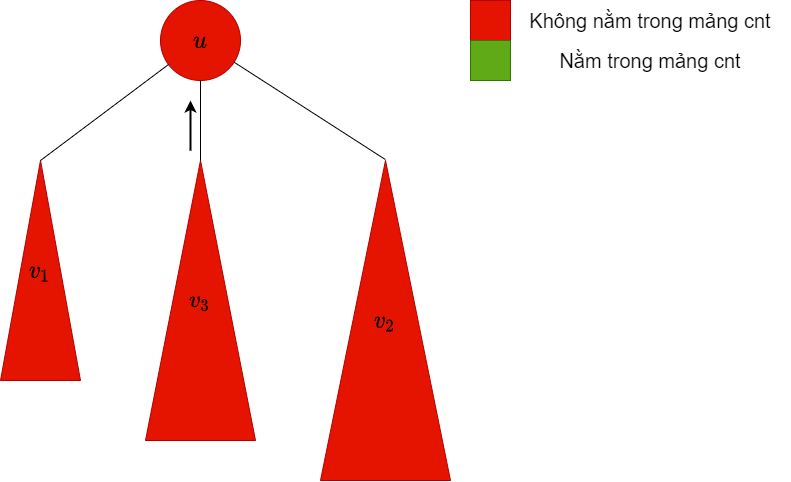dfs xuống cây con $v_2$, lúc này trong mảng $cnt$ chứa các màu trong cây con này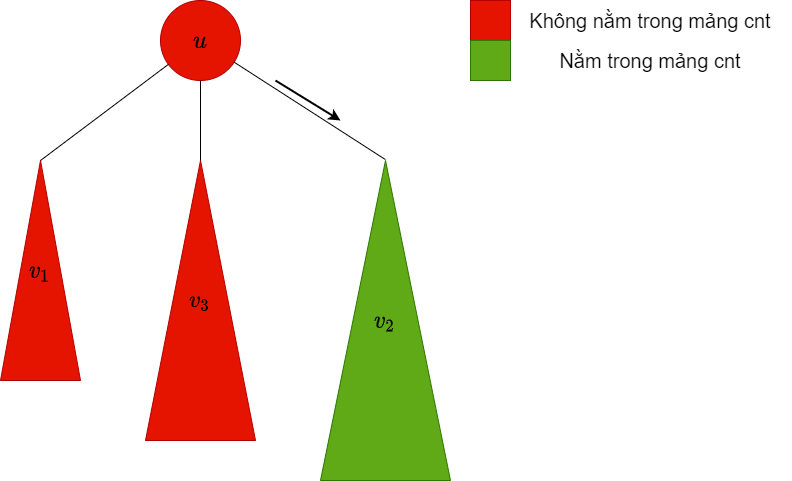
$v_2$ là `bigChild`, do đó ta giữ nguyên các màu trong cây con này trong mảng $cnt$
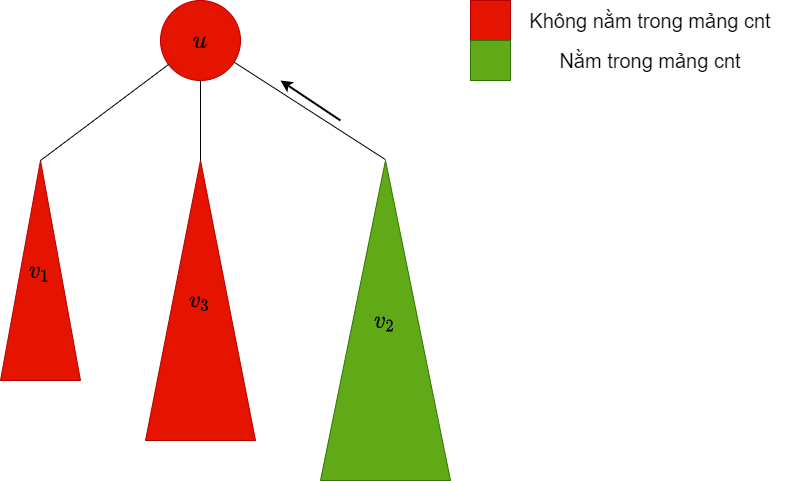Thêm các màu trong cây con $v_1$ vào mảng $cnt$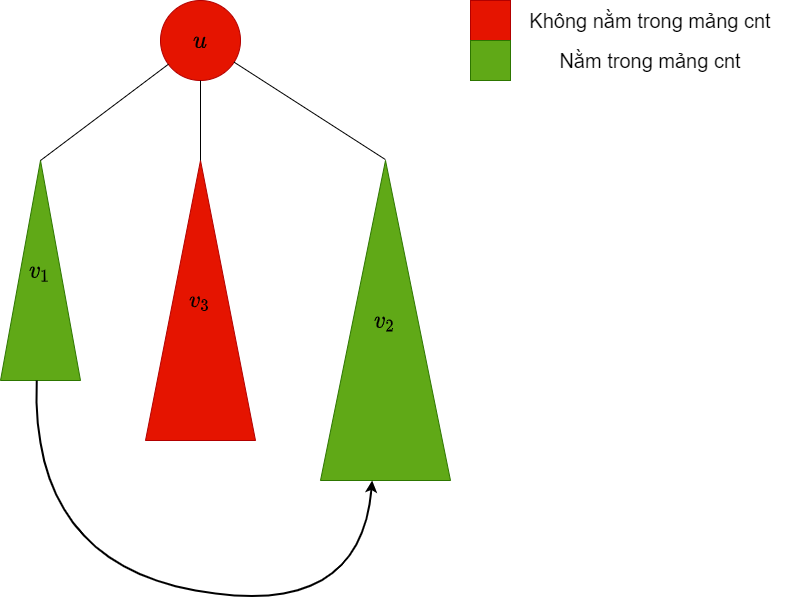
Thêm các màu trong cây con $v_3$ vào mảng $cnt$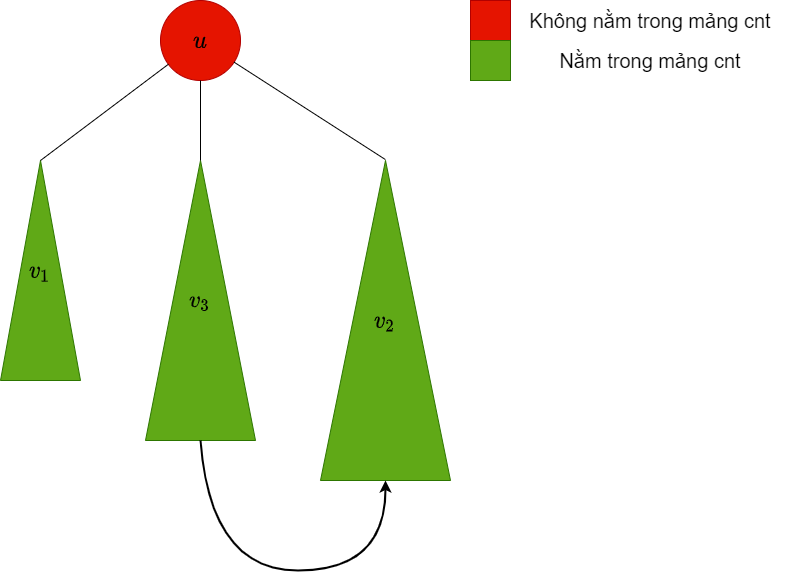
Thêm đỉnh $u$ vào mảng $cnt$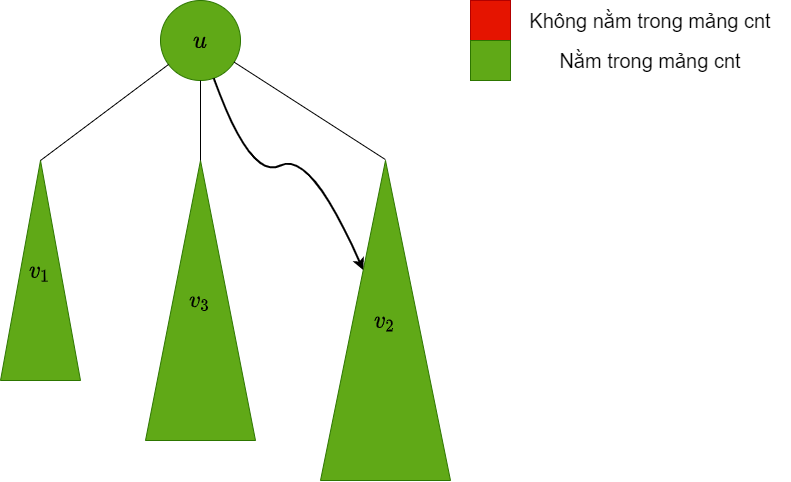

Lúc này mảng $cnt$ đã có đủ các màu trong cây con gốc $u$ và ta có thể trả lời các truy vấn của đỉnh $u$.

Code mẫu

#include <bits/stdc++.h>

using namespace std;

const int N = 5e5 + 5;
int n, q, color[N];
int sz[N];
int cnt[N];
int res[N]; // res[i] là đáp án của truy vấn thứ i
vector<pair<int, int>> queries[N]; 
        // cặp (a, b) trong queries[v] có nghĩa là ở đỉnh v 
        // có truy vấn hỏi có bao nhiêu đỉnh trong cây con có màu a 
        // và số thứ tự của truy vấn là b
vector<int> g[N];

void pre_dfs(int u, int p) {
    sz[u] = 1;
    for (auto v : g[u]) if (v != p) {
        pre_dfs(v, u);
        sz[u] += sz[v];
    }
}

void update(int u, int p, int delta) {
    cnt[color[u]] += delta;
    for (auto v : g[u]) if (v != p) update(v, u, delta);
} 

void dfs(int u, int p) {
    int bigChild = -1;
    for (auto v : g[u]) if (v != p) {
        if (bigChild == -1 || sz[v] > sz[bigChild]) bigChild = v;
    }

    for (auto v : g[u]) if (v != p && v != bigChild) {
        dfs(v, u);
        update(v, u, -1);
    }
    if (bigChild != -1) dfs(bigChild, u);

    for (auto v : g[u]) if (v != p && v != bigChild) update(v, u, 1);
    cnt[color[u]]++;
    
    for (auto p : queries[u]) res[p.second] = cnt[p.first];
}

signed main() {

    ios_base::sync_with_stdio(false); cin.tie(NULL);

    cin >> n >> q;

    for (int i = 1; i <= n; i++) cin >> color[i];

    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        g[a].push_back(b);
        g[b].push_back(a);
    }

    for (int i = 1; i <= q; i++) {
        int v, c;
        cin >> v >> c;
        queries[v].push_back({c, i});
    }

    pre_dfs(1, 0);
    dfs(1, 0);

    for (int i = 1; i <= q; i++) cout << res[i] << "\n";

}

Disjoint Set Union

Giới thiệu

Bài toán

Cấu trúc dữ liệu Disjoint Set Union

Cài đặt "ngây thơ"

Tối ưu 1 - Gộp theo kích cỡ / độ cao

Tối ưu 2 - Nén đường đi

Độ phức tạp thời gian

Chứng minh độ phức tạp thời gian

Một cách cài đặt khác

Một số ứng dụng của DSU

Lưu thêm thông tin khác cho mỗi tập hợp

Bài toán xếp hàng

Bài toán

Lời giải

Code mẫu

Tối ưu thuật toán tìm cây khung nhỏ nhất trong đồ thị

Đảo ngược truy vấn

Bài toán

Lời giải

Code mẫu

Kiểm tra tính chất hai phía của đồ thị online

Bài toán

Lời giải

Một số kĩ thuật sử dụng tính chất của DSU

Kĩ thuật gộp set (Small-to-Large Merging)

Bài toán

Lời giải

Code mẫu

Kĩ thuật DSU trên cây (Sack)

Bài toán

Lời giải

Code mẫu

Tham khảo

Bài tập

Disjoint Set Union

Kỹ thuật Gộp set

Kỹ thuật DSU trên cây