Thuật toán tìm kiếm nhị phân
Nguồn: Topcoder
Người dịch:
- Nguyễn Nhật Minh Khôi - VNU University of Science. Biên soạn lại từ bản dịch của Vũ Thị Thiên Anh
Reviewer: Hoàng Xuân Nhật, Trần Quang Lộc
Tìm kiếm nhị phân (hay còn gọi là chặt nhị phân) là một trong số các thuật toán cơ bản của khoa học máy tính. Trong bài viết này, chúng ta sẽ xây dựng một nền tảng lý thuyết, sau đó đưa ra cách cài đặt thuật toán này một cách chuẩn xác.
Bài toán mở đầu: Tìm giá trị cho trước trong một dãy đã sắp xếp
Mở đầu, ta sẽ đến với bài toán sử dụng tìm kiếm nhị phân đơn giản nhất. Đề bài như sau:
Cho trước một dãy $A$ được sắp tăng dần, trả về vị trí của phần tử có giá trị $x$ trong $A$. Lưu ý: để đơn giản, ta giả sử các phần tử trong mảng $A$ có giá trị phân biệt.
Ví dụ
Đầu tiên, ta sẽ xét một ví dụ để thấy được tư tưởng của thuật toán.
Cho $A = [0, 5, 13, 19, 2, 41, 55, 68, 72, 81, 98]$ và $x = 55$, thuật toán sẽ diễn ra như hình dưới:
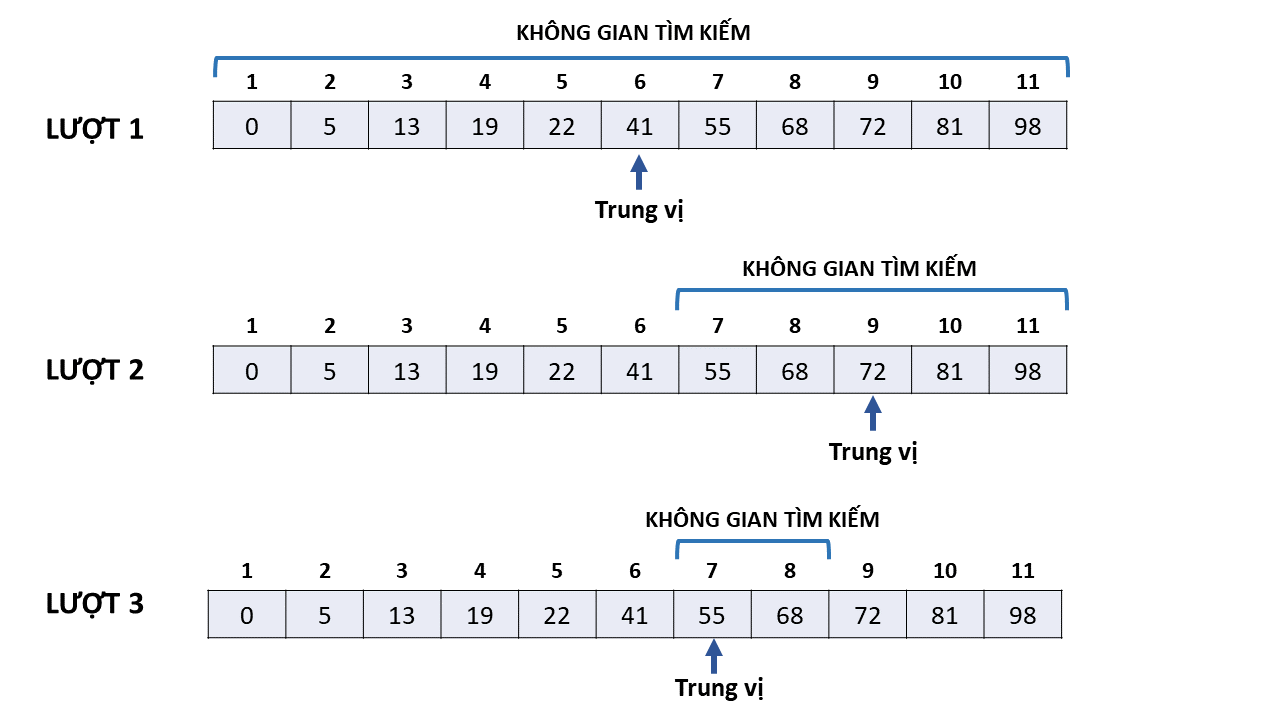
Ở lượt tìm đầu tiên, không gian tìm kiếm là tập hợp $S = {1,\ldots,11}$ gồm tất cả các chỉ số của mảng. Bắt đầu với việc chọn phần tử trung vị của không gian tìm kiếm hiện tại (chính là $6$), ta nhận xét $A[6]=41 < 55 = x$. Do theo đề bài mảng $A$ được sắp xếp tăng dần, ta biết được tất cả các phần tử có chỉ số $1,\ldots,6$ đều nhỏ hơn giá trị cần tìm $x$. Do đó, chúng chắc chắn không thể là kết quả, khi đó không gian tìm kiếm có thể thu hẹp lại $S = {7,\ldots,11}$, tức giảm đi một nửa.
Tương tự, ở lượt tìm thứ hai, ta xét phần tử trung vị của không gian tìm kiếm hiện tại (chính là $9$), nhận thấy $A[9]=72 > 55 = x$. Cũng do mảng $A$ được sắp xếp tăng dần, ta biết được tất cả các phần tử có vị trí từ $9,\ldots,11$ đều lớn hơn giá trị cần tìm $x$. Do đó, chúng chắc chắn không thể là kết quả, khi đó không gian tìm kiếm sẽ lại giảm đi một nửa $S = {7,\ldots,8}$.
Ở lượt tìm cuối cùng, ta cũng xét phần tử trung vị của không gian tìm kiếm hiện tại ở vị trí $7$ (ở đây số lượng phần tử của không gian tìm kiếm là chẵn, do đó có hai phần tử trung vị, ta có thể chọn một trong hai đều được, ở ví dụ này ta chọn phần tử trung vị đầu tiên), Nhận thấy $A[7] = 55 = x$, ta kết luận $5$ chính là vị trí của phần tử cần tìm và dừng thuật toán.
Tổng quát hóa bài toán
Từ ví dụ trên, ta có thể dễ dàng hiểu được ý tưởng của thuật toán tìm kiếm nhị phân. Đúng như tên gọi, thuật toán sẽ liên tục chia không gian tìm kiếm thành hai nửa và loại một nửa đi. Thuật toán có thể trình bày như sau:
- Ta duy trì một không gian tìm kiếm $S$ là một dãy con các giá trị có thể là kết quả (ở đây là chỉ số các phần tử trong $A$). Ban đầu, không gian tìm kiếm là toàn bộ các chỉ số của mảng $S={1,\ldots,n}$ với $n$ là chỉ số phần tử cuối cùng của $A$.
- Ở mỗi bước, thuật toán so sánh giá trị cần tìm với phần tử có chỉ số là trung vị trong không gian tìm kiếm. Dựa trên sự so sánh đó, cộng thêm việc ta biết dãy $A$ có thứ tự, ta có thể loại một nửa số phần tử của $S$. Lặp đi lặp lại quá trình này, cuối cùng ta sẽ được một không gian tìm kiếm bao gồm một phần tử duy nhất.
- Khi đó, nếu phần tử duy nhất đó bằng với giá trị cần tìm $x$ thì đó là nghiệm của bài toán, nếu không thì bài toán vô nghiệm.
Ở đây có hai lưu ý khi cài đặt thuật toán:
- Do không gian tìm kiếm luôn là một đoạn liên tục các giá trị nguyên, ta không cần lưu tất cả phần tử của không gian khi tìm kiếm mà chỉ cần duy trì hai biến
lowvàhightượng trưng cho phần tử đầu và cuối của đoạn. - Ta có thể tối ưu thuật toán hơn bằng việc dừng sớm nếu trong quá trình so sánh gặp một phần tử trung vị thỏa yêu cầu đề bài chứ không cần đợi đến khi không gian tìm kiếm chỉ còn một phần tử.
Dưới đây là code minh họa viết bằng ngôn ngữ C++. Trong trường hợp giá trị cần tìm không tồn tại trong khoảng tìm kiếm thì thuật toán sẽ trả về $-1$
int binary_search(int A[], int sizeA, int target) {
int lo = 1, hi = sizeA;
while (lo <= hi) {
int mid = lo + (hi - lo)/2;
if (A[mid] == target)
return mid;
else if (A[mid] < target)
lo = mid+1;
else
hi = mid-1;
}
// không tìm thấy giá trị target trong mảng A
return -1;
} Độ phức tạp thuật toán
Ở mỗi bước, kích thước không gian tìm kiếm bị giảm đi một nửa. Ta dễ thấy rằng độ phức tạp của thuật toán là $O(\log(N))$ với $N$ là số phần tử ban đầu của không gian tìm kiếm.
Hàm $\log$ là một hàm tăng rất chậm. Ví dụ như nếu phải tìm kiếm giá trị trong 1 triệu phần tử, với tìm kiếm nhị phân chỉ cần tối đa là 21 bước.
Tìm kiếm nhị phân trong thư viện chuẩn STL
C++ Standard Template Library đã cài đặt sẵn tìm kiếm nhị phân bằng các hàm lower_bound, upper_bound, binary_search, equal_range, bạn đọc có thể tham khảo tùy thuộc vào mục đích sử dụng.
Tìm kiếm nhị phân tổng quát
Ở phần trước, ta đã xét dạng đơn giản nhất của tìm kiếm nhị phân. Trong phần này, chúng ta sẽ tổng quát hóa thuật tìm kiếm nhị phân cho một lớp bài toán rộng hơn. Ta sẽ thấy tìm kiếm nhị phân có thể mở rộng để áp dụng cho bất kỳ loại hàm số đơn điệu nào nhận tham số đầu vào là số nguyên. Nói một cách đơn giản, một hàm số đơn điệu là một hàm tăng hoặc một hàm giảm. Trong ví dụ đầu bài, hiển nhiên mảng sắp xếp tăng có thể xem như một "hàm tăng".
Cơ sở lý thuyết: Định lý chính của tìm kiếm nhị phân
Khi gặp một bài toán mà ta đoán được có thể dùng tìm kiếm nhị phân để giải, thì ta phải chứng minh tính đúng đắn suy luận của chúng ta. Do đó, xây dựng một cơ sở lý thuyết vững chắc là vô cùng cần thiết. Sau đây, tôi sẽ trình bày một lớp tổng quát hóa nữa cho các bài toán có thể áp dụng tìm kiếm nhị phân, song song đó là ví dụ thực tế với bài toán mở đầu.
Cho không gian tìm kiếm $S$ bao gồm các ứng cử viên cho kết quả của bài toán. Ta định nghĩa môt hàm kiểm tra $P: S \rightarrow {\texttt{true}, \texttt{false}}$ là hàm nhận một ứng cử viên $x \in S$ và trả về giá trị $\texttt{true}/\texttt{false}$ cho biết $x$ có hợp lệ hay không (tùy vào bài toán mà định nghĩa hợp lệ sẽ khác nhau). Hiểu đơn giản, hàm $P$ là hàm "kiểm tra" một tính chất nào đó, xem một ứng cử viên cho kết quả của bài toán có thỏa tính chất đó không.
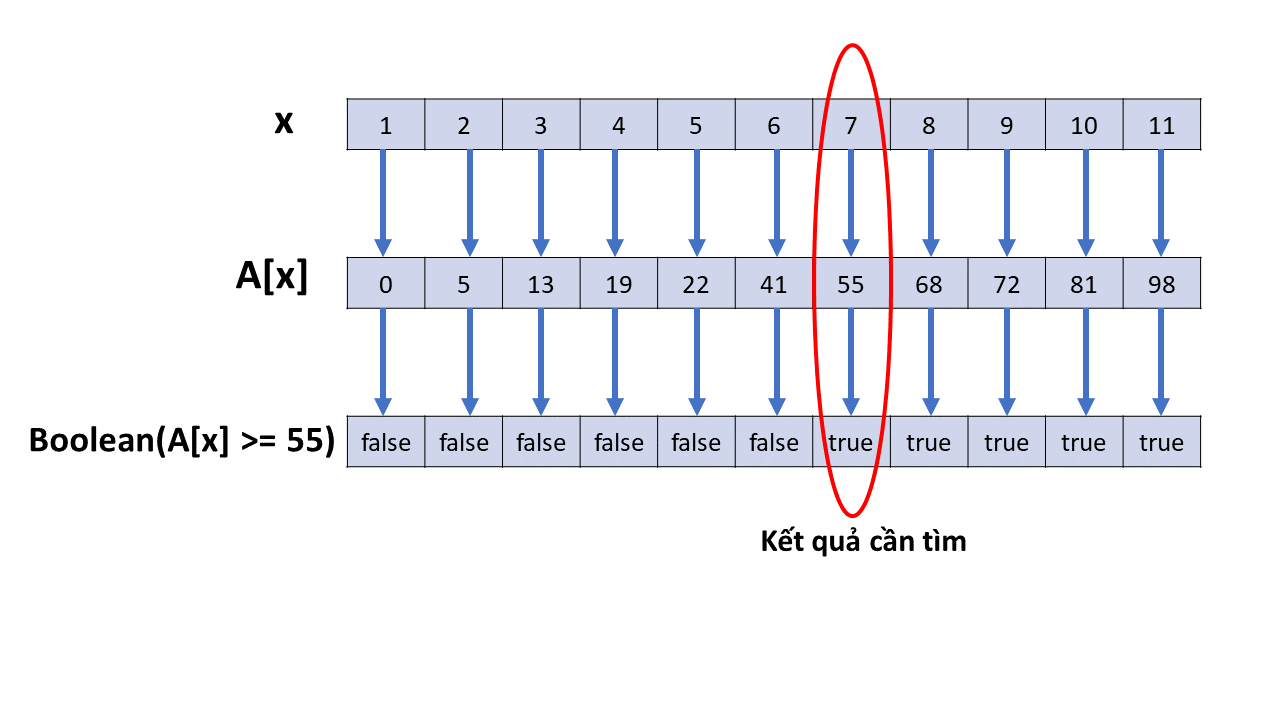
Với ví dụ ở đầu bài, thay vì tìm chỉ số của phần tử có giá trị $55$, ta có thể viết lại đề bài thành "tìm chỉ số nhỏ nhất sao cho phần tử ở chỉ số đó lớn hơn hoặc bằng $55$". Khi đó, không gian tìm kiếm ban đầu $S = {1,\ldots,11}$ (ban đầu mọi chỉ số của mảng đều có thể là kết quả) và $P(x) = boolean(a[x] \geq 55)$ trả về $\texttt{true}$ nếu $a[x] \geq 55$ và $\texttt{false}$ nếu $a[x] < 55$.
Định lý chính (Main Theorem) cho biết rằng: một bài toán chỉ có thể áp dụng tìm kiếm nhị phân nếu và chỉ nếu hàm kiểm tra $P$ của bài toán thỏa mãn \begin{equation} \forall x, y \in S, y > x \wedge P(x) = \texttt{true} \Rightarrow P(y) = \texttt{true} \tag{*} \label{eq:1} \end{equation}
Lưu ý rằng tính chất trên của hàm kiểm tra $P$ cũng tương đương với tính chất sau: \begin{equation} \forall x, y \in S, y < x \wedge P(x) = \texttt{false} \Rightarrow P(y) = \texttt{false} \tag{**} \label{eq:2} \end{equation}
Sự tương đương ở đây có thể chứng minh bằng phương pháp phản chứng, để tránh bài viết quá dài dòng, phần chứng minh để lại cho bạn đọc.
Định lý chính mang cho chúng ta một thông tin rất quan trọng, đó là điều kiện cần và đủ để một bài toán có thể giải bằng tìm kiếm nhị phân. Để hiểu được tại sao, chúng ta hãy phân tích kĩ hơn ý nghĩa tính chất của hàm $P$ mà định lý yêu cầu
- Tính chất $\eqref{eq:1}$ có thể giải thích như sau: nếu $x$ hợp lệ thì mọi phần tử $y > x$ đều hợp lệ. Tính chất này giúp chúng ta loại đi nửa sau của không gian tìm kiếm do đã biết chắc $x$ là phần tử nhỏ nhất trong nửa sau hợp lệ, ta ghi nhận $x$ là kết quả tạm thời và tiếp tục tìm xem có phần tử nào ở nửa đầu (nhỏ hơn $x$) hợp lệ hay không.
- Tương tự, tính chất $\eqref{eq:2}$ có thể giải thích như sau: nếu $x$ không hợp lệ thì mọi phần tử $y < x$ đều không hợp lệ. Tính chất này giúp chúng ta loại đi nửa trước của không gian tìm kiếm do đã biết chắc chúng không hợp lệ, ta chỉ quan tâm những phần tử ở nửa sau (lớn hơn $x$) mà ta chưa biết thông tin chúng có hợp lệ hay không.
Nếu ta tính giá trị $P(x)$ cho từng phần tử trong $S$ ban đầu, ta sẽ được một dãy liên tiếp các giá trị $\texttt{false}$ liền kề một dãy liên tiếp các giá trị $\texttt{true}$ (từ nay gọi là dãy $P(S)$). Dễ thấy ta có thể áp dụng tìm kiếm nhị phân trên dãy $P(S)$ mới này để tìm giá trị $x$ nhỏ nhất thỏa mãn $P(x) = \texttt{true}$ (hoặc cũng có thể làm cách tìm giá trị $x$ lớn nhất mà $P(x) = \texttt{false}$, tuy nhiên ở đây ta không chọn cách này).
Với ví dụ đầu bài, như đã nói $P(x) = boolean(A[x] \geq 55)$. Dễ thấy $P$ thỏa mãn tính chất đầu tiên, do $A$ được sắp tăng dần nên nếu $A[x] \geq 55$ thì chắc chắn các phần tử $y$ sau $x$ đều thỏa $A[y] \geq A[x] \geq 55$. Tương tự ta cũng suy ra được, nếu $A[x] < 55$ thì chắc chắn các phần tử $y$ trước $x$ đều thỏa $A[y] \leq A[x] < 55$. Áp dụng hàm $P(x) = boolean(A[x] \geq 55)$ cho từng phần tử của $S={1,\ldots,11}$ ta có hình sau
Chú ý rằng ta thấy có thể dễ dàng xây dựng định lý chính dựa trên một hàm kiểm tra $P$ ngược lại, tức $P(S)$ sẽ là một dãy $\texttt{true}$ liên tiếp theo sau bởi $\texttt{false}$ liên tiếp. Tuy nhiên, ở đây ta sẽ chỉ xét một trường hợp để bài viết ngắn gọn hơn, trường hợp còn lại có thể làm tương tự.
Từ định lý trên, ta rút ra được mấu chốt để giải một bài toán dùng tìm kiếm nhị phân là ta cần thiết kế được hàm $P$ hợp lý sao cho thỏa mãn điều kiện trong định lý chính.
Cuối cùng, tại sao ta phải tốn công tổng quát hóa thuật toán này thay vì dùng cách làm đơn giản ở ví dụ đầu? Đó là vì nhiều bài toán không thể ở dưới dạng tìm kiếm một giá trị cụ thể, nhưng ta lại có thể định nghĩa một hàm kiểm tra thỏa yêu cầu định lý chính để có thể áp dụng tìm kiếm nhị phân. Bằng cách đó, ta có thể mở rộng lớp bài toán có thể giải bằng tìm kiếm nhị phân.
Ví dụ điển hình cho việc áp dụng định lý là với bài toán Tìm căn bậc hai, thay vì hỏi "Số $x$ nào bình phương lên thì bằng $a$?" và tìm kiếm tuần tự tất cả các trường hợp, ta có thể định nghĩa hàm $P(x)$ trả lời cho câu hỏi "$x^2$ có lớn hơn hoặc bằng $a$ hay không?" sau đó dùng tìm kiếm nhị phân để tìm $x$ nhỏ nhất thỏa mãn. Với cách làm này ta có thể đơn giản hóa bài toán thành một bài toán yes/no, hơn thế còn giảm độ phức tạp của bài toán từ $O(n)$ xuống chỉ còn $O(\log(n))$.
Cài đặt thuật toán tổng quát
Trước khi cài đặt thuật toán, ta phải trả lời những câu hỏi sau:
- Dãy $P(S)$ của bạn có dạng $\texttt{false}-\texttt{true}$ ($\texttt{false}$ liên tiếp rồi $\texttt{true}$ liên tiếp) hay $\texttt{true}-\texttt{false}$ (ngược lại)? Ở cài đặt phía dưới sẽ mặc định dãy $P(S)$ có dạng $\texttt{false}-\texttt{true}$, vì vậy nếu dãy $P(S)$ của bạn có dạng $\texttt{true}-\texttt{false}$, hãy đảo hàm $P(x)$ của bạn ngược lại.
- Bài của bạn có luôn có nghiệm không? Nếu không hãy kiểm tra trước khi tìm kiếm nhị phân để tiết kiệm chi phí tính toán.
- Mục tiêu của bạn là tìm phần tử $\texttt{false}$ lớn nhất hay tìm phần tử $\texttt{true}$ nhỏ nhất? Ở đây sẽ trình bày cả hai cách.
- Nếu bài toán có nghiệm, hãy đảm bảo giá trị chặn dưới và chặn trên của khoảng tìm kiếm (biến
lovàhi) là bắt đầu và kết thúc của một khoảng đóng mà chắc chắn chứa kết quả cần tìm (phần tử $x$ đầu tiên mà $P(x) = \texttt{true}$). Hãy đảm bảo điều kiện này trong lúc thu hẹp không gian tìm kiếm để tránh xảy ra lỗi. - Phạm vi tìm kiếm đã đủ rộng chưa? Sẽ có nhiều lúc chấm xong bạn nhận ra là mình thiếu vài trường hợp biên. Vì thời gian chạy chỉ tăng theo hàm logarit $O(\log(N))$, bạn hoàn toàn có thể nâng rộng khoảng tìm kiếm ra mà ít khi lo bị quá thời gian. Tuy nhiên, phải để ý các lỗi như tràn mảng, tràn số,…
- Luôn kiểm tra trường hợp $P(S) = [\texttt{false},\texttt{true}]$. Để hiểu lý do tại sao hãy đọc Trường hợp 2 của cài đặt.
TH1: tìm $x$ nhỏ nhất mà $P(x) = \texttt{true}$. Dưới đây là đoạn code mẫu viết bằng C++.
bool P(int x) {
// Logic của hàm P ở đây
return true; // thay giá trị này bằng giá trị đúng logic.
}
int binary_search(int lo, int hi) {
while (lo < hi) {
int mid = lo + (hi-lo)/2;
if (P(mid) == true)
hi = mid;
else
lo = mid+1;
}
if (P(lo) == false)
return -1; // P(x) = false với mọi x thuộc S, bài toán vô nghiệm.
return lo; // lo là giá trị x nhỏ nhất mà P(x) = true
}Khi $P(mid) = \texttt{true}$, ta có thể bỏ nửa sau của không gian tìm kiếm vì đã biết phần tử trong đó luôn hợp lệ. Tuy nhiên ta vẫn phải giữ $mid$ trong không gian tìm kiếm mới vì nó có thể là phần tử đầu tiên mà $P = \texttt{true}$. Do đó không gian tìm kiếm mới sẽ là $S={lo, mid}$, ta gán $hi = mid$.
Tương tự, khi $P(mid) = \texttt{false}$, ta có thể bỏ nửa đầu (bao gồm cả phần tử $mid$) vì tất cả các phần tử này đều không hợp lệ. Lúc này không gian tìm kiếm mới sẽ là $S={mid + 1, hi}$, ta gán $lo = mid+1$.
TH2: tìm $x$ lớn nhất mà $P(x) = \texttt{false}$, suy luận tương tự như trên, ta có đoạn code như sau:
bool P(int x) {
// Logic của hàm P ở đây
return true; // thay giá trị này bằng giá trị đúng logic.
}
int binary_search(int lo, int hi) {
while (lo < hi) {
int mid = lo + (hi-lo+1)/2;
if (P(mid) == true)
hi = mid - 1;
else
lo = mid;
}
if (P(lo) == true)
return -1; // P(x) = true với mọi x thuộc S, bài toán vô nghiệm.
return lo; // lo là giá trị x lớn nhất mà P(x) = false
}Bạn sẽ thắc mắc rằng tại sao cách tính $mid$ lại có một tí khác biệt so với thuật toán đầu tiên. Để hiểu được tại sao ta phải làm thế, ta sẽ xét trường hợp sau: trong quá trình tìm kiếm, nếu tại một thời diểm nào đó mà dãy $P(S)$ tạo ra bởi các phần tử của không gian tìm kiếm có dạng như sau
| false | true |
Nếu ta tính $mid = lo + (hi-lo)/2$, đoạn code sẽ lặp vô hạn. Nó sẽ luôn chọn phần tử trung vị là $mid = lo$, nhưng cận dưới $lo$ sẽ không di chuyển vì nó muốn giữ lại phần tử có $p = \texttt{false}$ thỏa yêu cầu tìm kiếm đó. Do đó, ta thay đổi công thức tính $mid$ thành $mid = lo + (hi-lo+1)/2$, làm như vậy sẽ khiến cận dưới sẽ được làm tròn lên thay vì làm tròn xuống, khi đó nó có thể loại bỏ phần tử $\texttt{true}$ trước khi xét phần tử $\texttt{false}$. Có nhiều cách làm khác để thực hiện điều này, tuy nhiên, đây là cách dễ hiểu nhất. Do vậy, hãy luôn luôn kiểm tra thử trường hợp $P(S) = [\texttt{false}, \texttt{true}]$.
Một điều có thể bạn đang thắc mắc nữa là tại sao để tìm trung vị ta tính $mid = lo + (hi-lo)/2$ chứ không phải $mid = (hi+lo)/2$. Sở dĩ phải làm như vậy là để tránh khả năng xảy ra lỗi làm tròn số nguyên, ta muốn phép chia được làm tròn xuống, về gần với cận dưới, tuy nhiên phép chia làm tròn khác khi có số âm, nên nếu $(lo+hi)$ là số âm thì kết quả sẽ bị làm tròn lên. Code như trong mẫu kia giúp quá trình tính toán đều được làm tròn đúng theo logic. Đối với các bài toán mà chỉ cần xử lý giá trị dương thì lỗi này không xảy ra.
Cài đặt thuật toán với nửa khoảng
Cài đặt với đoạn đóng $[lo, hi]$ như trên có ưu điểm là dễ hiểu. Tuy nhiên, quay lại một chút với cơ sở lý thuyết: với dãy $P(S)$ có dạng $\texttt{false}-\texttt{true}$, thực tế ta nên chọn giá trị $lo$ và $hi$ mà $P(lo) = \texttt{false}$ và $P(hi) = \texttt{true}$ để đảm bảo luôn tìm được nghiệm. Do đó sẽ không ổn nếu như dãy $P(S)$ của ta đều toàn giá trị $\texttt{false}$ (tức vô nghiệm). Trong trường hợp này, cài đặt với đoạn đóng có thêm đoạn kiểm tra để return - 1.
Giải pháp cho trường hợp này chính là cài đặt với nửa khoảng. Để ý rằng trong trường hợp vô nghiệm, cách cài đặt với khoảng đóng sẽ trả về cận trên $hi$ của đoạn tìm kiếm ban đầu (do chỉ có cận dưới $lo$ liên tục dịch chuyển lên và chạm tới $hi$). Hơn nữa, thuật toán của ta không bao giờ gọi $P(hi)$ vì để có $mid = hi$, ta đã phải có $lo = hi$, nhưng lúc đó thuật toán chắc chắn đã dừng do điều kiện while (lo < hi) trong cài đặt.
Điều này cho ta một ý tưởng: tạo một giá trị $hi' = hi + 1$ ảo và mặc định coi $P(hi') = \texttt{true}$. Ta sẽ tìm kiếm nhị phân trên đoạn $[lo, hi']$ mới và nếu bài toán vô nghiệm thì kết quả trả về sẽ là $hi'$, ta không cần phải kiểm tra để return -1. Sở dĩ gọi là cài đặt với nửa khoảng vì khi truyền tham số cho hàm là $lo$ và $hi$, thực ra ta chỉ muốn kết quả trong nửa khoảng $[lo, hi)$, còn $hi$ chỉ là giá trị ảo cho biết trường hợp vô nghiệm.
Cài đặt cũng tương tự với đoạn đóng, ngoại trừ việc ta loại bỏ đi đoạn code kiểm tra vô nghiệm:
bool P(int x) {
// Logic của hàm P ở đây
return true; // thay giá trị này bằng giá trị đúng logic.
}
// nhớ rằng ta phải truyền hi lớn hơn một đơn vị
// so với đoạn tìm kiếm thực sự
int binary_search(int lo, int hi) {
while (lo < hi) {
int mid = lo + (hi-lo)/2;
if (P(mid) == true)
hi = mid;
else
lo = mid+1;
}
return lo; // lo là giá trị x nhỏ nhất mà P(x) = true
}binary_search(0, N) với $N$ là số phần tử của mảng. Toàn bộ thư viện STL, lower_bound, upper_bound đều nhận nửa khoảng, và thực tế nguyên lý của các hàm đó cũng như trên: không tìm ra đáp án thì trả về iterator end.
Lưu ý: Với trường hợp ta muốn tìm vị trí phần tử $\texttt{false}$ cuối cùng thì nửa khoảng cần tìm sẽ là (lo, hi] và hàm sẽ tự động trả về lo nếu mọi giá trị trong khoảng là $\texttt{true}$.
Ví dụ
Đến đây ta sẽ áp dụng những điều vừa học vào một bài cụ thể Leetcode 1011.
Trong bài này, một băng chuyền phải vận chuyển các gói hàng theo thứ tự cho trước trong $days$ ngày. Gói hàng thứ $i$ có trọng lượng $weights[i]$. Biết mỗi ngày băng chuyền chỉ có thể vận chuyển tổng khối lượng tối đa là $MAX$. Đề bài yêu cầu tìm $MAX$ nhỏ nhất để băng chuyền có thể hoàn thành nhiệm vụ được giao.
Để ý thấy rằng, với một số $MAX$, ta có thể tính toán được số ngày để chuyển hết các gói hàng sao cho mỗi ngày tổng khối lượng vận chuyển không quá $MAX$. Ban đầu, giao gói hàng $1$ để ngày $1$ chuyển. Nếu vận chuyển gói hàng $2$ trong ngày $1$ không làm tổng khối lượng trong ngày vượt $MAX$, thì ta sẽ chuyển luôn gói đó trong ngày $1$. Nếu không, ta sẽ chuyển gói đó trong ngày $2$. Làm lần lượt như thế tới khi mọi gói hàng đều được chuyển, ta sẽ có được số ngày tối thiểu cần để chuyển hết gói hàng với tổng khối lượng mỗi ngày không quá $MAX$.
Quay lại đề bài, ta thấy rằng thực ra vấn đề của bài toán là tìm số $MAX$ nhỏ nhất sao cho số ngày tối thiểu để chuyển hết gói hàng không quá $days$ ngày. Như vậy, ta có thể dùng tìm kiếm nhị phân với hàm kiểm tra $P$ được xây dựng bằng thuật toán tham lam được trình bày ở trên để kiểm tra các giá trị $MAX$. Để ý tính chất đơn điệu ở đây thể hiện ở chỗ nếu $MAX$ tăng lên thì số lượng ngày cần dùng chỉ có thể giữ nguyên hoặc giảm đi nên hàm $P$ thỏa định lý chính và có thể áp dụng tìm kiếm nhị phân.
Sau đây là đoạn code mẫu bằng C++:
// hàm kiểm tra P
bool check(int capacity, const vector<int>& weights, int days) {
int current_weight = 0; --days;
for(int i = 0; i < weights.size(); ++i) {
if (current_weight + weights[i] <= capacity)
current_weight += weights[i];
else {
--days;
current_weight = weights[i];
}
}
return days >= 0;
}
// hàm tìm kiếm nhị phân
int shipWithinDays(const vector<int>& weights, int days) {
int lo = 0, hi = 0;
for (int i = 0; i < weights.size(); ++i) {
lo = max(lo, weights[i]);
hi += weights[i];
}
while (lo < hi) {
int mid = lo + (hi - lo)/2;
if (check(mid, weights, days))
hi = mid;
else
lo = mid + 1;
}
return lo;
}Hàm tìm kiếm nhị phân chính là hàm shipWithinDays và hàm kiểm tra là hàm check.
Có một lưu ý về việc chọn cận dưới và cận trên. Cận trên có thể là bất cứ số nguyên nào đủ lớn, ở đây chọn là tổng của tất cả các gói hàng (cho trường hợp tệ nhất cần vận chuyển trong đúng một ngày). Tuy nhiên cận dưới phải bằng ít nhất là khối lượng của gói hàng nặng nhất để tránh trường hợp gói hàng quá lớn để chuyển trong một ngày.
Để kiểm tra thuật toán không bị lặp vô hạn với trường hợp $[\texttt{false}, \texttt{true}]$, ta thử một test như sau: $weights = [1,1], days = 1$ và thấy thuật toán hoạt động tốt.
Độ phức tạp thuật toán là $O(n \cdot \log(SIZE))$ với $SIZE = hi -lo + 1$ là kích thước của không gian tìm kiếm và $n$ là số lượng gói hàng, do đó thuật toán chạy rất nhanh.
Tìm kiếm nhị phân trên số thực
Tìm kiếm nhị phân cũng có thể được áp dụng khi không gian tìm kiếm là một đoạn số thực. Thường thì việc xử lý sẽ đơn giản hơn với số nguyên do ta không phải bận tâm về việc dịch chuyển cận:
bool P(double x) {
// Logic của hàm P ở đây
return true; // thay giá trị này bằng giá trị đúng logic.
}
bool isTerminated(double lo, double hi) {
// trả về kết quả của việc kiểm tra
// lo và hi có thỏa điều kiện dừng chưa
}
double binary_search(double lo, double hi) {
while (isTerminated(lo, hi) == false) {
double mid = lo + (hi-lo)/2;
if (P(mid) == true)
hi = mid;
else
lo = mid;
}
// trung bình cộng lo và hi xấp xỉ
// ranh giới giữa false và true
return lo + (hi-lo)/2;
}
isTerminated. Thông thường có 2 cách quyết định khi nào dừng vòng lặp:
- Dừng sau một số vòng lặp cố định (fixed): thông thường khi làm bài tập trên TopCoder, chỉ cần lặp khoảng 100 lần là đủ (nhiều khi là thừa) để đạt được độ chính xác mong muốn cho những bài dạng thế này.
- Sai số tuyệt đối (absolute error): dừng khi $hi - lo \leq \epsilon$ ($\epsilon$ thường rất nhỏ, khoảng $10^{-8}$). Cách này được sử dụng nếu thời gian chặt và bạn phải tiết kiệm số lần lặp.