Bao lồi (Convex Hull)
Nguồn: wcipeg
Tác giả:
- Lê Minh Hoàng - Đại học Khoa học Tự nhiên, ĐHQG-HCM
Reviewer:
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên, ĐHQG-HCM
- Ngô Nhật Quang - HUS High School for Gifted Students
Giới thiệu
Trong hình học tính toán (computational geometry), bao lồi (convex hull) của một tập điểm là tập lồi (convex set) nhỏ nhất (theo diện tích, thể tích, …) mà tất cả các điểm đều nằm trong tập đó.
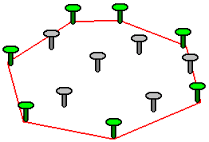
Theo một cách trực quan, nếu ta coi những điểm trong một tập hợp là những cái đinh đóng trên một tấm gỗ, bao lồi của tập điểm đó có viền ngoài tạo bởi sợi dây chun mắc vào những cái đinh sau khi bị kéo căng về các phía.
Các thuật toán tìm bao lồi trên mặt phẳng
Bài toán tìm bao lồi của một tập điểm trên mặt phẳng là một trong những bài toán được nghiên cứu nhiều nhất trong hình học tính toán và có rất nhiều thuật toán để giải bài toán này. Sau đây là ba thuật toán phổ biến nhất, được giới thiệu theo thứ tự tăng dần về độ khó.
Chú ý 1: Bạn đọc nên xem qua Hình học tính toán phần 1 và Hình học tính toán phần 2 trước khi tiếp tục để biết về các khái niệm cơ bản.
Chú ý 2: Bạn đọc nên hiểu phần thuật toán trước khi đọc phần cài đặt để dễ hiểu hơn.
Thuật toán bọc gói quà (Gift wrapping algorithm)
Thuật toán bọc gói quà, hay còn gọi là thuật toán Jarvis march, là một trong những thuật toán tìm bao lồi đơn giản và dễ hiểu nhất. Tên thuật toán xuất phát từ sự tương tự của thuật toán với việc đi bộ xung quanh các điểm và cầm theo một dải băng gói quà.
 |
|---|
| source: wikipedia - Gift wrapping algorithm |
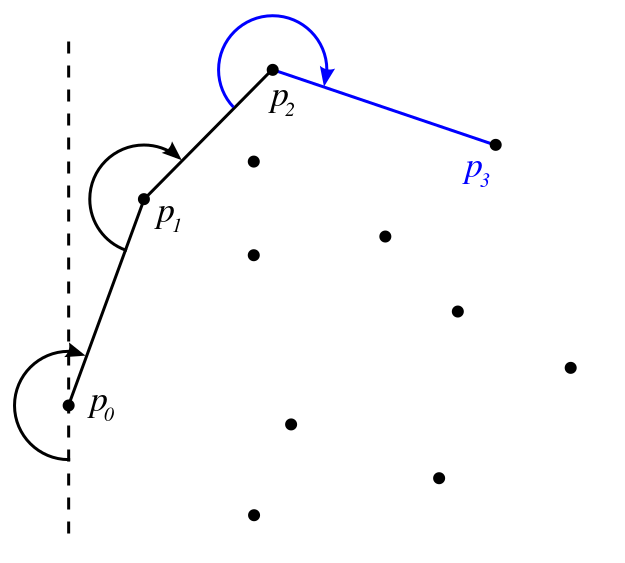
Thuật toán này được mô tả như sau:
- Bước đầu:
- Chọn $P$ là điểm trái nhất trong tập các điểm (để đảm bảo $P$ nằm trong tập bao lồi).
- Chọn hướng ta đang nhìn $\vec{v}$ là từ hướng dưới lên trên.
- Tiếp theo, các bước sẽ lặp lại đến khi tìm được bao lồi:
- Ta quay $\vec{v}$ theo chiều kim đồng hồ cho đến khi ta nhìn thấy một điểm, gọi điểm đó là $Q$.
- Ta cầm theo dải băng và đi đến điểm $Q$.
- Khi ta đến $Q$, ta thay:
- $\vec{v}$ thành $\overrightarrow{PQ}$
- $P$ thành $Q$
- Thuật toán kết thúc khi ta trở về điểm ban đầu. Lúc này ta đã đi đến tất cả các đỉnh của bao lồi theo chiều kim đồng hồ.
Với mỗi lần tìm $Q$, ta duyệt qua tất cả các điểm $R$ trong tập và tính góc tạo bởi $\vec{v}$ và $\overrightarrow{PR}$, vì vậy độ phức tạp của mỗi lần tìm điểm là $\mathcal{O}(n)$, với $n$ là số lượng điểm trong tập. Gọi số điểm thuộc bao lồi là $h$, Khi đó độ phức tạp của thuật toán là $\mathcal{O}(nh)$
 |
|---|
| Minh hoạ của thuật toán bọc gói quà source: wikipedia - Gift wrapping algorithm |
Cài đặt
Nhược điểm của cách cài đặt này là sai số của số thực khi tính góc.
#include <bits/stdc++.h>
using namespace std;
const double EPS = 1e-9;
// Kiểu điểm
struct Point {
int x, y;
Point(int x = 0, int y = 0) : x(x), y(y) {}
bool operator==(const Point &o) {
return x == o.x && y == o.y;
}
bool operator!=(const Point &o) {
return !(*this == o);
}
Point operator-(const Point &o) {
return Point(x - o.x, y - o.y);
}
double length() const {
return sqrt(1LL * x * x + 1LL * y * y);
}
};
// Tích vô hướng của vector A và vector B
long long dot(const Point &A, const Point &B) {
return 1LL * A.x * B.x + 1LL * A.y * B.y;
}
// Góc giữa vector A và vector B
double calcAngle(const Point &A, const Point &B) {
return acos(dot(A, B) / A.length() / B.length());
}
// Trả về bao lồi với thứ tự các điểm được liệt kê cùng chiều kim đồng hồ
vector<Point> convexHull(vector<Point> p, int n) {
if (n <= 2) return p;
// Đưa điểm trái nhất lên đầu tập
for (int i = 1; i < p.size(); ++i) {
if (p[0].x > p[i].x) swap(p[0], p[i]);
}
// Tập bao lồi
vector<Point> hull;
hull.push_back(p[0]);
// Dựng bao lồi
do {
// Đỉnh cuối của tập hull
Point P = hull.back();
// Đỉnh kế cuối của tập hull
// Nếu hull.size() == 1 thì đặt đỉnh kế cuối là (P.x, P.y - 1)
// Vì ban đầu hướng đang nhìn là từ dưới lên trên
Point P0 = (hull.size() == 1 ? Point(P.x, P.y - 1) : hull[hull.size() - 2]);
// Q là đỉnh tiếp theo của tập hull
Point Q = p[0];
double angle = calcAngle(P0 - P, Q - P);
for (int i = 1; i < n; ++i) {
if (Q == P || Q == P0) {
Q = p[i];
angle = calcAngle(P0 - P, Q - P);
continue;
}
if (p[i] == P || p[i] == P0) continue;
double newAngle = calcAngle(P0 - P, p[i] - P);
// Nếu góc (P0, P, Q) nhỏ hơn góc (P0, P, p[i]) thì gán Q = p[i]
if (abs(angle - newAngle) > EPS) {
if (angle < newAngle) {
Q = p[i];
angle = newAngle;
}
}
else {
if ((Q - P).length() > (p[i] - P).length()) {
Q = p[i];
angle = newAngle;
}
}
}
hull.push_back(Q);
} while (hull[0] != hull.back());
// Đỉnh đầu tiên lặp lại ở cuối 1 lần
hull.pop_back();
return hull;
}Thuật toán Graham (Graham scan)
Thuật toán Graham có độ phức tạp trong trường hợp xấu nhất nhỏ hơn thuật toán bọc gói, song thuật toán Graham lại phức tạp hơn.
- Đầu tiên, ta xác định một điểm mà chắc chắn thuộc bao lồi. Thông thường, khi cài đặt người ta chọn điểm có tung độ nhỏ nhất (nếu có nhiều điểm như vậy thì chọn điểm trái nhất). Gọi điểm này là điểm $O$.
- Chọn hệ trục tọa độ có gốc là điểm $O$ vừa chọn, sắp xếp các điểm còn lại theo thứ tự tăng dần của góc tạo bởi trục hoành theo chiều dương và $\overrightarrow{OI}$ với $I$ là một trong các điểm còn lại.
- Gọi tập bao lồi hiện tại là $H$ và điểm cuối của tập bao lồi $H$ là $H_h$ (ban đầu $h = 1$, tức tập $H$ chỉ chứa $O$).
- Duyệt theo thứ tự các điểm vừa sắp xếp. Với mỗi điểm ta sửa lại bao lồi $H$:
- Thêm điểm $P$ vào cuối bao lồi $H$ (tức là ta tăng $h$ lên $1$ và đặt $H_h = P$).
- Nếu $h < 3$, ta bỏ qua bước $3$ và xét điểm tiếp theo.
- Xét $3$ điểm $H_{h-2}, H_{h-1}$ và $H_h$. Gọi $\vec{u} = \overrightarrow{H_{h-2}H_{h-1}}$ và $\vec{v} = \overrightarrow{H_{h-1}H_h}$.
- Nếu $\vec{u}\times\vec{v}>0$, tức là thứ tự của $H_{h-2}, H_{h-1}$, $H_h$ là ngược chiều kim đồng hồ, thì cả $3$ điểm đều tạm thời thuộc bao lồi $H$, và ta xét điểm tiếp theo.
- Nhưng nếu $\vec{u}\times\vec{v}<0$, tức là góc $\widehat{H_{h-2}H_{h-1}H_h}$ sẽ tạo ra phần lõm, thì ta bỏ điểm $H_{h-1}$ ra khỏi bao lồi $H$ (tức là ta đặt $H_{h-1} = H_h$ giảm $h$ đi $1$) và quay lại bước $2$.
Về độ phức tạp thuật toán, ta thấy bước sắp xếp các điểm có độ phức tạp $\mathcal{O}(n\log{n})$. Mỗi điểm được thêm/xoá nhiều nhất một lần nên tổng độ phức tạp của các bước thêm/xoá điểm là $\mathcal{O}(n)$. Vậy độ phức tạp của thuật toán Graham là $\mathcal{O}(n\log{n})$, phù hợp cho hầu hết các bài toán.
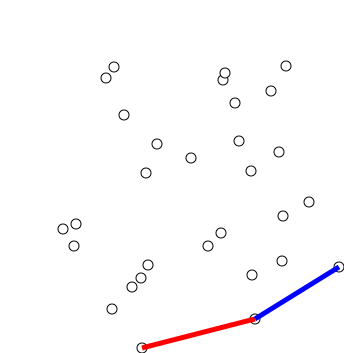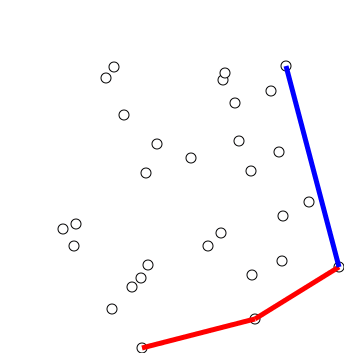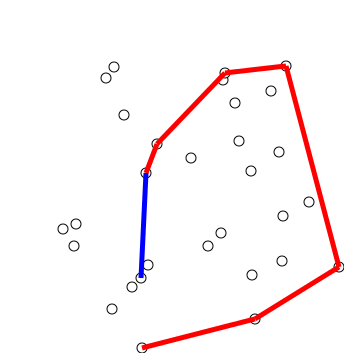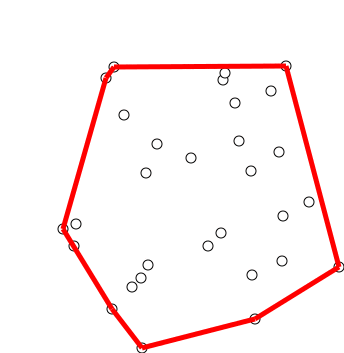 |
|---|
| Minh hoạ của thuật toán Graham source: wikipedia - Graham scan |
Cài đặt
#include <bits/stdc++.h>
using namespace std;
// Kiểu điểm
struct Point {
int x, y;
};
// Tích có hướng của AB và AC
long long cross(const Point &A, const Point &B, const Point &C) {
return 1LL * (B.x - A.x) * (C.y - A.y) - 1LL * (C.x - A.x) * (B.y - A.y);
}
// A -> B -> C đi theo thứ tự theo chiều kim đồng hồ (-1), thẳng hàng (0), ngược chiều kim đồng hồ (1)
int ccw(const Point &A, const Point &B, const Point &C) {
long long S = cross(A, B, C);
if (S < 0) return -1;
if (S == 0) return 0;
return 1;
}
// Trả về bao lồi với thứ tự các điểm được liệt kê ngược chiều kim đồng hồ
vector<Point> convexHull(vector<Point> p, int n) {
// Đưa điểm có tung độ nhỏ nhất (và trái nhất) lên đầu tập
for (int i = 1; i < n; ++i) {
if (p[0].y > p[i].y || (p[0].y == p[i].y && p[0].x > p[i].x)) {
swap(p[0], p[i]);
}
}
// Sắp xếp các điểm I theo góc tạo bởi trục hoành theo chiều dương và OI
sort(p.begin() + 1, p.end(), [&p](const Point &A, const Point &B) {
int c = ccw(p[0], A, B);
if (c > 0) return true;
if (c < 0) return false;
return A.x < B.x || (A.x == B.x && A.y < B.y);
});
// Tập bao lồi
vector<Point> hull;
hull.push_back(p[0]);
// Dựng bao lồi
for (int i = 1; i < n; ++i) {
while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p[i]) < 0) {
hull.pop_back();
}
hull.push_back(p[i]);
}
return hull;
}Thuật toán chuỗi đơn điệu (Monotone chain algorithm)
Thuật toán chuỗi đơn điệu vừa dễ cài đặt, vừa là thuật toán nhanh nhất trong $3$ thuật toán được giới thiệu trong bài này. Thuật toán dựa trên việc tìm hai chuỗi đơn điệu của bao lồi: bao trên (hay chuỗi trên) và bao dưới (hay chuỗi dưới).
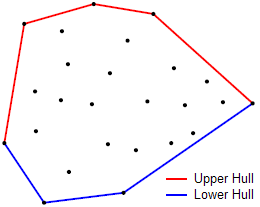 |
|---|
| source: wikibooks - Monotone chain |
Ta thấy điểm ở xa về phía bên trái nhất (từ đây gọi là điểm trái nhất) và điểm ở xa về phía bên phải nhất (từ đây gọi là điểm phải nhất) luôn thuộc bao lồi. Phần bao lồi theo chiều kim đồng hồ tính từ điểm trái nhất đến điểm phải nhất gọi là bao trên trên, phần còn lại của bao lồi gọi là bao dưới. Ta sẽ tìm bao trên và bao dưới độc lập với nhau.
- Bước đầu tiên, ta sắp xếp các điểm được cho theo thứ tự tăng dần theo hoành độ. Nếu hai điểm có cùng hoành độ, điểm có tung độ nhỏ hơn sẽ đứng trước. Sau bước này thì điểm trái nhất sẽ ở đầu và điểm phải nhất sẽ ở cuối tập điểm.
- Ta xét việc xây dựng bao trên. Gọi $H$ là bao trên hiện tại và độ lớn của bao là $h$. Điểm đầu của bao là $H_1$ và điểm cuối của bao là $H_h$. Xét từng điểm $P$ theo thứ tự đã sắp xếp:
- Thêm $P$ vào cuối bao trên $H$.
- Nếu $h < 3$, ta bỏ qua bước $3$ và xét điểm tiếp theo.
- Xét $3$ điểm $H_{h-2}, H_{h-1}$ và $H_h$. Gọi $\vec{u} = \overrightarrow{H_{h-2}H_{h-1}}$ và $\vec{v} = \overrightarrow{H_{h-1}H_h}$.
- Nếu $\vec{u}\times\vec{v}<0$, tức là thứ tự của $H_{h-2}, H_{h-1}$, $H_h$ là cùng chiều kim đồng hồ, thì cả $3$ điểm đều tạm thời thuộc bao trên $H$, và ta xét điểm tiếp theo.
- Nhưng nếu $\vec{u}\times\vec{v}>0$, tức là góc $\widehat{H_{h-2}H_{h-1}H_h}$ sẽ tạo ra phần lõm ở bao trên, thì ta bỏ điểm $H_{h-1}$ ra khỏi bao lồi $H$ và quay lại bước $2$.
Sau khi xét hết các điểm, $H$ sẽ chứa toàn bộ phần bao trên. Sau đó, ta tìm chuỗi bao dưới bằng cách tương tự, chỉ khác là ta xét các điểm theo thứ tự ngược lại (tức là ta xét điểm phải nhất trước). Lưu ý không thêm điểm phải nhất hai lần. Khi thuật toán kết thúc, $H$ sẽ chứa tất cả các đỉnh của bao lồi, với điểm đầu được lặp lại ở cuối.
Thuật toán này cũng có độ phức tạp $\mathcal{O}(n\log{n})$. Thuật toán chuỗi đơn điệu được khuyên dùng ở mọi bài toán tìm bao lồi, do nó đơn giản hơn thuật toán Graham và nhanh hơn một chút (do ta không phải tính góc).
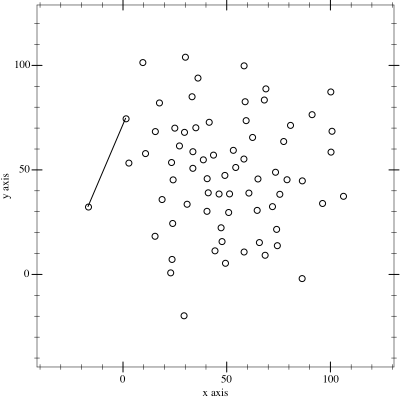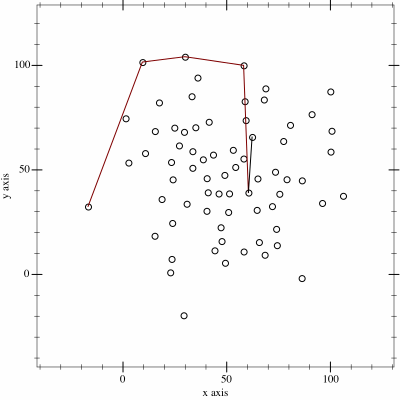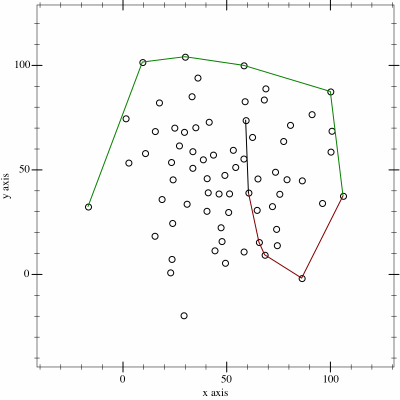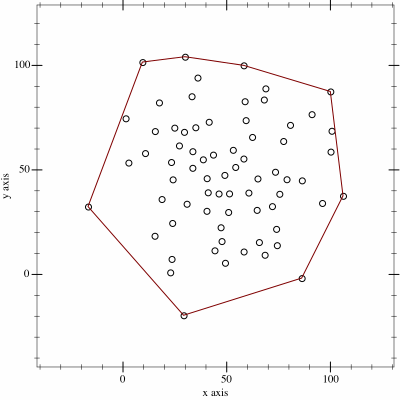 |
|---|
| Minh hoạ của thuật toán chuỗi đơn điệu source: wikibooks - Monotone chain |
Cài đặt
Link bài tập: CSES - Convex Hull
#include <bits/stdc++.h>
using namespace std;
// Kiểu điểm
struct Point {
int x, y;
};
// A -> B -> C đi theo thứ tự ngược chiều kim đồng hồ
bool ccw(const Point &A, const Point &B, const Point &C) {
return 1LL * (B.x - A.x) * (C.y - A.y) - 1LL * (C.x - A.x) * (B.y - A.y) > 0;
}
// Trả về bao lồi với thứ tự các điểm được liệt kê theo chiều kim đồng hồ
vector<Point> convexHull(vector<Point> p, int n) {
// Sắp xếp các điểm theo tọa độ x, nếu bằng nhau sắp xếp theo y
sort(p.begin(), p.end(), [](const Point &A, const Point &B) {
if (A.x != B.x) return A.x < B.x;
return A.y < B.y;
});
// Tập bao lồi
vector<Point> hull;
hull.push_back(p[0]);
// Dựng bao trên
for (int i = 1; i < n; ++i) {
while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p[i])) {
hull.pop_back();
}
hull.push_back(p[i]);
}
// Tiếp tục dựng bao dưới
for (int i = n - 2; i >= 0; --i) {
while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p[i])) {
hull.pop_back();
}
hull.push_back(p[i]);
}
// Xoá đỉểm đầu được lặp lại ở cuối
if (n > 1) hull.pop_back();
return hull;
}
int main() {
int n;
cin >> n;
vector<Point> p(n);
for (Point &a : p) {
cin >> a.x >> a.y;
}
vector<Point> hull = convexHull(p, n);
cout << hull.size() << '\n';
for (Point p : hull) {
cout << p.x << ' ' << p.y << '\n';
}
}Xử lí trường hợp suy biến
Các thuật toán trên hoạt động tốt trong trường hợp lí tưởng, tức là không có hai điểm nào trùng nhau và không có ba điểm nào thẳng hàng. Tuy nhiên, trong hầu hết các bài toán, ta sẽ phải xử lí các điểm trùng nhau và các bộ ba điểm thẳng hàng. Biện luận tất cả các trường hợp sẽ là một công việc khó nhằn và nhàm chán. Vì vậy, hãy ghi nhớ những điều sau:
- Đọc kĩ đề bài để biết được dữ liệu vào có bị suy biến hay không, nếu có thì rơi vào trường hợp nào (lưu ý rằng không phải đề bài nào cũng nói rõ rằng dữ liệu bị suy biến).
- Nếu tồn tại các điểm trùng nhau:
- Thuật toán bọc gói
- Vấn đề về phép chia cho số $0$ (bởi vì tồn tại $\vec{0}$ nên phần tính góc gặp vấn đề).
- Thuật toán Graham và thuật toán chuỗi đơn điệu
- Nếu ta phải in ra các đỉnh của bao lồi, có ba thứ tự in các đỉnh mà đề bài có thể hỏi: cùng chiều kim đồng hồ (cw), ngược chiều kim đồng hồ (ccw), hoặc theo thứ tự xuất hiện trong dữ liệu vào.
- Nếu đề bài yêu cầu in các đỉnh theo thứ tự xuất hiện trong dữ liệu vào, đề bài có thể yêu cầu in ra đỉnh đầu tiên xuất hiện trong dữ liệu vào nếu các đỉnh trùng nhau, hoặc in ra tất cả các đỉnh.
- Thuật toán bọc gói
- Nếu có các bộ ba điểm thẳng hàng:
- Đề bài yêu cầu bao lồi có số lượng đỉnh tối đa hay tối thiểu, từ đó mà ta quyết định có nên cho thêm các điểm thuộc cạnh của bao lồi hay không.
- Thuật toán bọc gói: Chọn điểm xa nhất hay gần nhất nếu có hai điểm cùng số đo góc nhỏ nhất.
- Thuật toán Graham và thuật toán chuỗi đơn điệu: Đổi CCW thành CW và ngược lại.
- Đề bài yêu cầu bao lồi có số lượng đỉnh tối đa hay tối thiểu, từ đó mà ta quyết định có nên cho thêm các điểm thuộc cạnh của bao lồi hay không.
- Diện tích bao lồi bằng $0$. Có hai trường hợp như vậy: tất cả các điểm đều trùng nhau, hoặc tất cả điểm đều thẳng hàng.
Bao lồi 3D
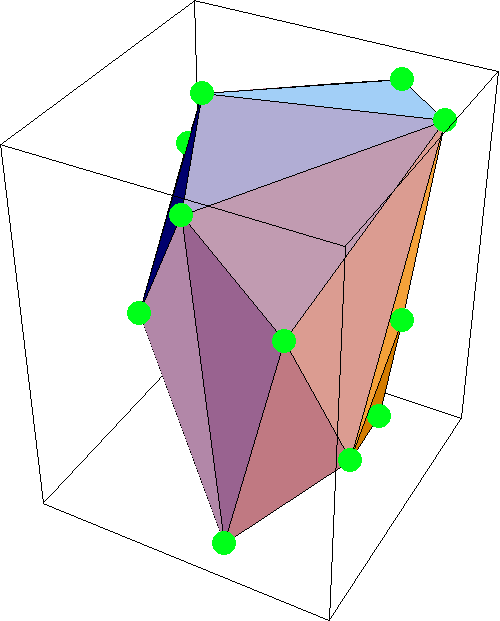
Tìm bao lồi trong 3D thực sự là một bài toán khó. Bài toán này chắc chắn sẽ không bao giờ được ra trong IOI, và học sinh trung học không cần phải đi sâu vào vấn đề này. Tuy nhiên, có một thuật toán $\mathcal{O}(n^2)$ khá là đơn giản:
- Đầu tiên, ta tìm hình chiếu của các điểm trên mặt phẳng $Oxy$, và tìm một cạnh chắc chắn thuộc bao bằng cách lấy một điểm có tung độ lớn nhất rồi tìm điểm kia bằng cách chạy vòng lặp của thuật toán bọc gói một lần. Đây là phần đầu tiên của bao lồi.
- Sau đó, xét cạnh vừa tìm được, tìm một điểm thứ ba để tạo thành một mặt tam giác của bao lồi. Ta chọn điểm thứ ba bằng cách tìm điểm để tất cả các điểm khác nằm ở phía bên phải của mặt tam giác đó (giống như thuật toán bọc gói, ta tìm cạnh để tất cả các điểm khác đều nằm về phía bên phải cạnh đó).
- Bây giờ ta đã có ba cạnh trong bao lồi, ta chọn ngẫu nhiên một trong ba cạnh đó, rồi tìm tiếp một tam giác với cạnh này, rồi tiếp tục cho đến khi không còn cạnh nào nữa (khi ta tìm thêm một mặt tam giác, ta phải thêm hai cạnh vào bao, tuy vậy hai cạnh này phải chưa có trong bao, nếu không ta phải đi tìm hai cạnh khác).
- Có tổng cộng $\mathcal{O}(n)$ mặt, và mỗi lần duyệt các điểm ta mất thời gian $\mathcal{O}(n)$ vì ta phải duyệt tất cả các điểm còn lại, do đó độ phức tạp của thuật toán là $\mathcal{O}(n^2)$. (Nếu bạn nghĩ bạn có thể cài đặt được thuật toán này, hãy nộp bài tại SPOJ - CH3D).
- Ta có thể tăng tốc độ thuật toán này bằng các loại bỏ các điểm chắc chắn không phải đỉnh của bao (tìm các điểm cực theo các trục tọa độ, rồi loại bỏ các điểm nằm trong bát diện mà các đỉnh đấy tạo ra).
Ta có thể tìm bao lồi trong không gian với độ phức tạp $\mathcal{O}(n\log{n})$ bằng phương pháp chia để trị, tuy nhiên việc cài đặt thuật toán này là vô cùng khó.
Ứng dụng
VNOJ - KMIX
Tóm tắt
Có $N$ loại cocktail khác nhau, mỗi loại có nồng độ cam và dâu lần lượt là $x$ và $y$ (tính theo đơn vị phần tỉ). Có $M$ vị khách, vị khách thứ $i$ yêu cầu loại cocktail có nồng độ cam và dâu lần lượt là $x$ và $y$. Hỏi có thể đáp ứng yêu cầu của từng vị khách hay không?
Ý tưởng
Nếu xem mỗi loại cocktail là một điểm toạ độ $(x, y)$ trên mặt phẳng, vậy các loại cocktail có thể pha chế từ $2$ loại cocktail $i$ và $j$ khác nhau sẽ nằm trên đoạn thẳng nối $2$ điểm $(x_i, y_i)$ và $(x_j, y_j)$. Mở rộng, các loại cocktail có thể pha chế từ $N$ loại cocktail ban đầu sẽ nằm trong bao lồi của $N$ điểm $(x, y)$.
Để kiểm tra nhanh một điểm có nằm trong bao lồi hay không trong $\mathcal{O}(\log{n})$, ta thực hiện như sau:
- Gọi tập bao lồi là $H$, giả sử tập $H$ được liệt kê theo chiều kim đồng hồ.
- Đầu tiên, ta kiểm tra $(H_0, H_1, P)$ có ngược chiều kim đồng hồ hay không ($P$ thoả thuộc vùng màu xanh).
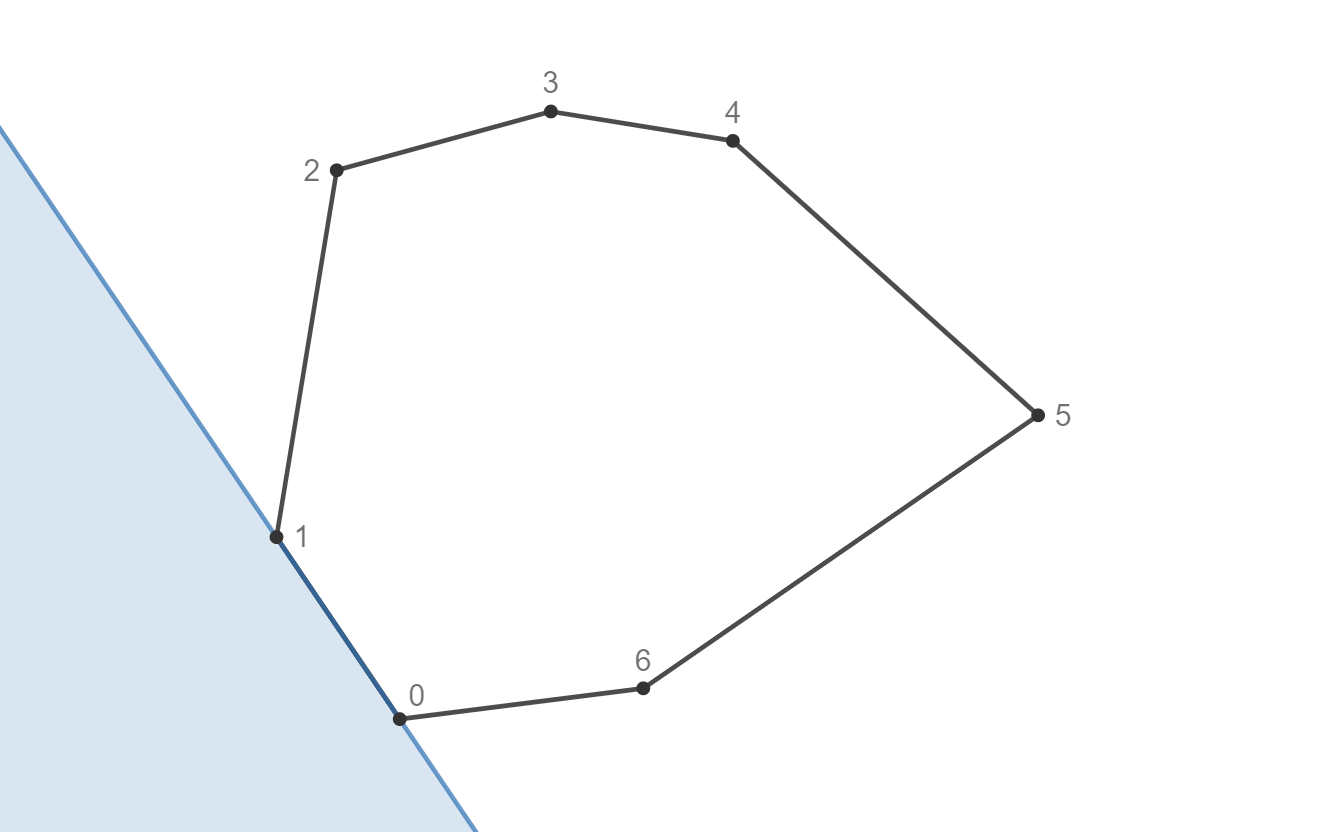
- Tiếp theo, ta kiểm tra $(H_{n-1}, H_0, P)$ có ngược chiều kim đồng hồ hay không ($P$ thoả thuộc vùng màu cam).
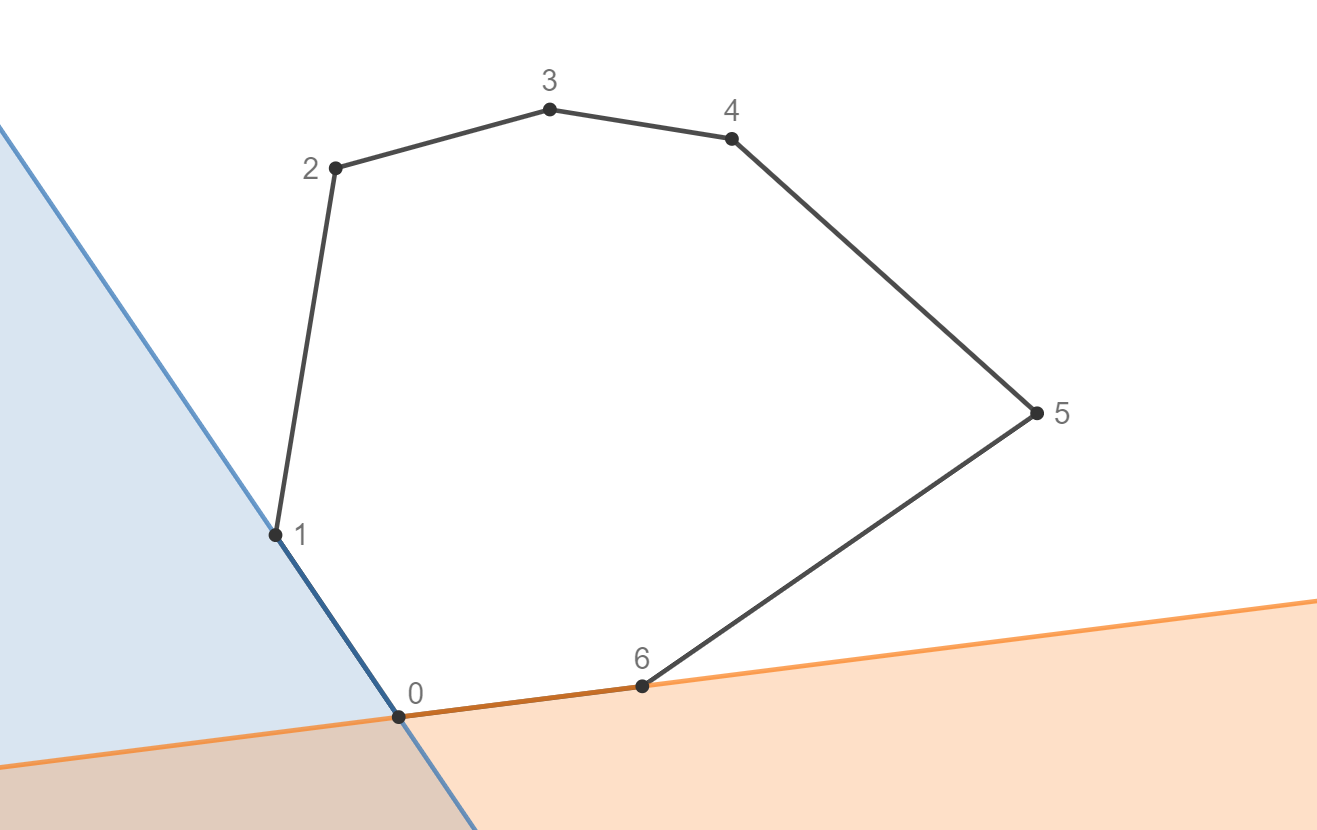
- Bây giờ, ta chặt nhị phân để tìm tia $\overrightarrow{H_0H_x}$ thoả mãn $\overrightarrow{H_0H_x}$ là tia gần điểm $P$ nhất ở phía bên phải bằng cách kiểm tra $CCW(H_0,H_x,P)$ (chi tiết xem ở phần cài đặt).
- Sau khi có $x$ (ví dụ $x=4$), ta biết được rằng $P$ thuộc vùng tạo bởi $2$ tia $\overrightarrow{H_0H_{x-1}}$ và $\overrightarrow{H_0H_x}$ (vùng màu tím).
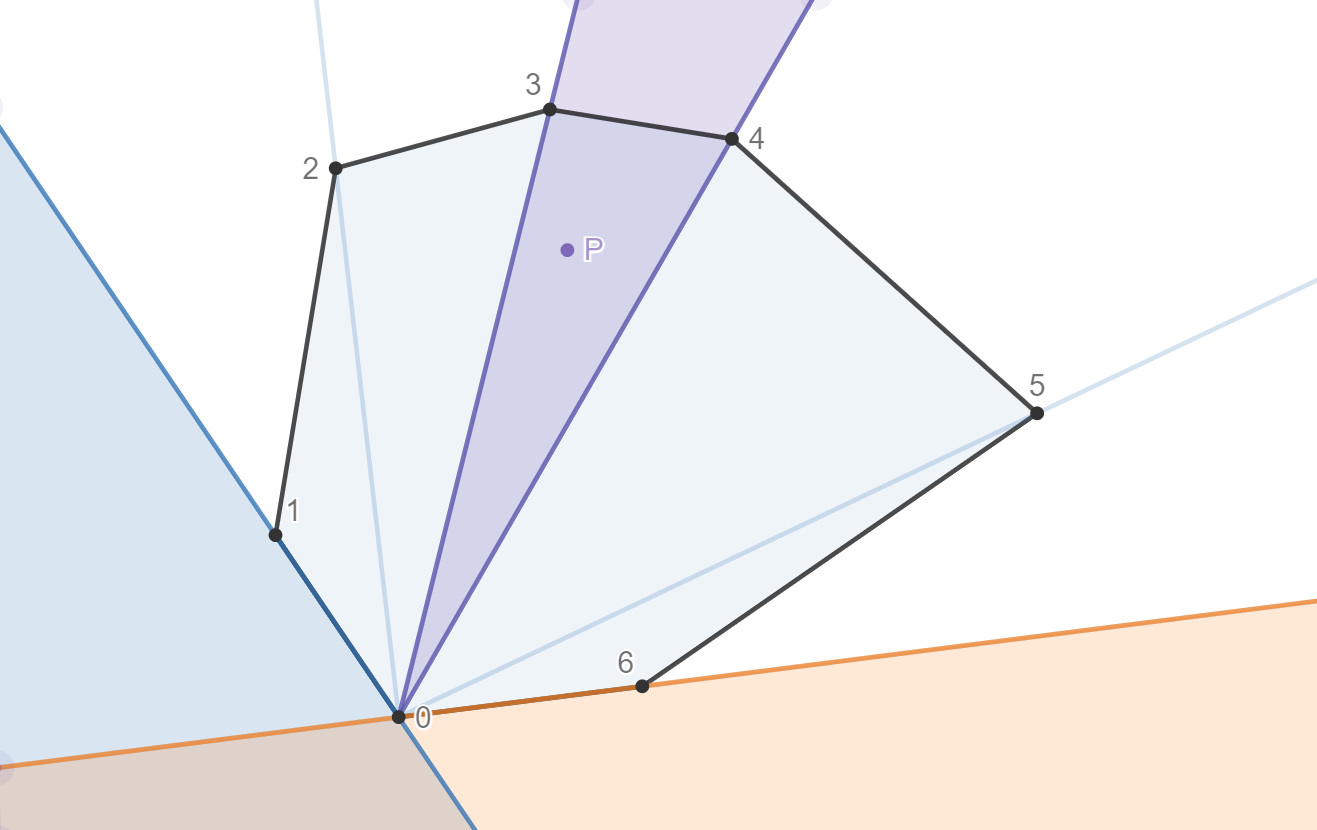
- Đến đây, ta kiểm tra $(H_{x-1}, H_x, P)$ có cùng chiều kim đồng hồ hay không (tức $P$ có thuộc tam giác $(H_0,H_{x-1},H_x)$ hay không).
Cài đặt
#include <bits/stdc++.h>
using namespace std;
// Kiểu điểm
struct Point {
int x, y;
bool operator==(const Point &o) {
return x == o.x && y == o.y;
}
};
// Tích có hướng của AB và AC
long long cross(const Point &A, const Point &B, const Point &C) {
return 1LL * (B.x - A.x) * (C.y - A.y) - 1LL * (C.x - A.x) * (B.y - A.y);
}
// Tích vô hướng của AB và AC
long long dot(const Point &A, const Point &B, const Point &C) {
return 1LL * (B.x - A.x) * (C.x - A.x) + 1LL * (B.y - A.y) * (C.y - A.y);
}
// C nằm trên đoạn AB nếu ABxAC = 0 và CA.CB <= 0
bool onSegment(const Point &A, const Point &B, const Point &C) {
return cross(A, B, C) == 0 && dot(C, A, B) <= 0;
}
// A -> B -> C đi theo thứ tự cùng chiều kim đồng hồ
bool cw(const Point &A, const Point &B, const Point &C) {
return cross(A, B, C) < 0;
}
// A -> B -> C đi theo thứ tự ngược chiều kim đồng hồ
bool ccw(const Point &A, const Point &B, const Point &C) {
return cross(A, B, C) > 0;
}
// Trả về bao lồi với thứ tự các điểm được liệt kê theo chiều kim đồng hồ
vector<Point> convexHull(vector<Point> p, int n) {
// Sắp xếp các điểm theo tọa độ x, nếu bằng nhau sắp xếp theo y
sort(p.begin(), p.end(), [](const Point &A, const Point &B) {
if (A.x != B.x) return A.x < B.x;
return A.y < B.y;
});
// Tập bao lồi
vector<Point> hull;
hull.push_back(p[0]);
// Dựng bao trên
for (int i = 1; i < n; ++i) {
while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p[i])) {
hull.pop_back();
}
hull.push_back(p[i]);
}
// Tiếp tục dựng bao dưới
for (int i = n - 2; i >= 0; --i) {
while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p[i])) {
hull.pop_back();
}
hull.push_back(p[i]);
}
// Xoá đỉểm đầu được lặp lại ở cuối
if (n > 1) hull.pop_back();
return hull;
}
// Kiểm tra P có nằm trong bao lồi hull hay không
bool checkInHull(vector<Point> &hull, Point P) {
int n = hull.size();
// Xử lý trường hợp suy biến có diện tích bao lồi = 0
if (n == 1) return (hull[0] == P);
if (n == 2) return onSegment(hull[0], hull[1], P);
// Nếu (hull[0], hull[1], P) ngược chiều kim đồng hồ thì P nằm ngoài bao lồi
if (ccw(hull[0], hull[1], P)) return false;
// Nếu (hull[n - 1], hull[0], P) không cùng chiều kim đồng hồ thì P chỉ thoả
// nếu P nằm trên đoạn (hull[n - 1], hull[0])
if (!cw(hull[n - 1], hull[0], P)) {
return onSegment(hull[n - 1], hull[0], P);
}
// Tìm x thoả mãn tia (hull[0], hull[x]) là tia gần nhất ở phía bên phải của P
int lo = 2, hi = n - 1, x = -1;
while (lo <= hi) {
int mid = (lo + hi) >> 1;
// Nếu (hull[0], hull[mid], P) ngược chiều kim đồng hồ thì
// tia (hull[0], hull[mid]) nằm ở phía bên phải của P
if (ccw(hull[0], hull[mid], P)) {
x = mid;
hi = mid - 1;
}
else lo = mid + 1;
}
// P nằm trong tam giác (hull[0], hull[x - 1], hull[x])
// nếu (hull[x - 1], hull[x], P) không ngược chiều kim đồng hồ
return !ccw(hull[x - 1], hull[x], P);
}
int main() {
int n;
cin >> n;
vector<Point> p(n);
for (Point &a : p) {
cin >> a.x >> a.y;
}
vector<Point> hull = convexHull(p, n);
int m;
cin >> m;
while (m--) {
Point P;
cin >> P.x >> P.y;
cout << (checkInHull(hull, P) ? "YES\n" : "NO\n");
}
}