Kĩ thuật bao lồi (Convex Hull Trick)
Nguồn: P3G
Tác giả: Phan Minh Hoàng + Lê Anh Đức
Kĩ thuật bao lồi là kĩ thuật (hoặc là cấu trúc dữ liệu) dùng để xác định hiệu quả, có tiền xử lý, cực trị của một tập các hàm tuyến tính tại một giá trị của biến độc lập. Mặc dù tên gọi giống nhưng kĩ thuật này lại khá khác biệt so với thuật toán bao lồi của hình học tính toán.
Ngoài ra có một kĩ thuật liên quan đến kĩ thuật bao lồi là IT đoạn thẳng
Lịch sử
Kĩ thuật bao lồi được biết đến nhiều nhất có lẽ vì nó cần để ăn trọn toàn bộ số điểm trong nhiều bài toán USACO, như là bài Acquire trong bảng gold của USACO tháng 3 năm 2008. Thuật toán được đưa vào các cuộc thi lập trình một cách rộng rãi sau bài Batch Scheduling trong kì thi IOI 2002. Đây là một kĩ thuật khá lạ và ít có nguồn trên mạng về vấn đề này.
Bài toán cơ bản
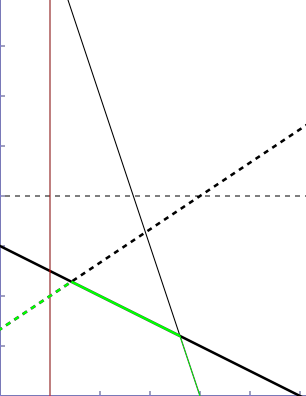
Cho một tập lớn các hàm tuyến tính có dạng $y = m_i x + b_i$ và một số lượng lớn truy vấn. Mỗi truy vấn là một số $x$ và hỏi giá trị cực tiểu $y$ có thể đạt được nếu chúng ta thế $x$ vào một trong những phương trình đã cho. Ví dụ, cho các phương trình $y=4$, $y=\frac{4}{3}+\frac{2}{3}x$, $y=12-3x$ và $y=3-\frac{1}{2}x$ và truy vấn $x=1$. Chúng ta phải tìm phương trình mà trả về giá trị cực tiểu hoặc giá trị cực tiểu đó (trong trường hợp này là phương trình $y=\frac{4}{3}+\frac{2}{3}x$ và giá trị cực tiểu đó là 2).
Biến thể của bài toán có thể là tìm giá trị cực đại có thể giải quyết với một thay đổi nhỏ vì vậy trong bài viết này chỉ tập trung vào bài toán tìm giá trị cực tiểu.
Sau khi ta vẽ các đường thẳng lên hệ trục tọa độ, dễ thấy rằng: chúng ta muốn xác định, tại $x=1$(đường màu đỏ) đường nào có tọa độ $y$ nhỏ nhất. Ở trong trường hợp này là đường nét đứt đậm $y=\frac{4}{3}+\frac{2}{3}x$.
Thuật toán duyệt
Với mỗi truy vấn trong $Q$ truy vấn, ta duyệt qua từng hàm số và thử từng từng hàm và xem thử hàm nào trả giá trị cực tiểu cho giá trị $x$. Nếu có $M$ đường thẳng và $Q$ truy vấn, độ phức tạp của thuật toán sẽ $\mathcal{O}(MQ)$. Kĩ thuật bao lồi sẽ giúp giảm độ phức tạp xuống còn $\mathcal{O}((Q+M)\log M$, một độ phức tạp hiệu quá hơn nhiều.
Kĩ thuật
Xét hình vẽ ở trên. Đường thẳng $y=4$ sẽ không bao giờ là giá trị nhỏ nhất với tất cả giá trị của $x$. Mỗi đường trong mỗi đường thẳng còn lại sẽ lại trả lại giá trị cực tiểu trong một và chỉ một đoạn liên tiếp (có thể có một biên là $+\infty$ hoặc $-\infty$). Đường chấm đậm sẽ cho giá trị cực tiểu với tất cả giá trị nằm bên trái điểm giao với đường đen đậm. Đường đen đậm sẽ cho giá trị cực tiểu với tất cả giá trị giữa giao điểm của nó với đường nhạt và đường chấm đậm. Và đường nhạt sẽ nhận cực tiểu cho tất cả giá trị bên phải giao điểm với đường đậm. Một nhận xét nữa là với giá trị của $x$ càng tăng thì hệ số góc của các hàm số sẽ giảm, $\frac{2}{3}, \frac{-1}{2}, -3$. Với một chút chứng minh dễ thấy rằng điều này luôn đúng.
Điều này giúp chúng ta hiểu phần nào thuật toán:
-
Bỏ đi các đường thẳng không quan trọng như $y=4$ trong ví dụ (những đường thẳng mà không nhận giá trị cực tiểu trong bất kì đoạn nào)
-
Sắp xếp các đoạn thẳng còn lại theo hệ số góc và được một tập $N$ đoạn thẳng (của $N$ đường thẳng còn lại) mà mỗi đoạn có một đường thẳng nhận giá trị cực tiểu.
-
Dùng thuật toán tìm kiếm nhị phân cơ bản để có thể tìm kiếm đáp án cho từng truy vấn.
Ý nghĩa của tên kĩ thuật
Cụm từ bao lồi được sử dụng để chỉ hình bao trên/dưới (upper / lower envelope). Trong ví dụ, nếu chúng ta coi mỗi phần đoạn thẳng tối ưu của đường thẳng (bỏ qua đường $y=4$), chúng ta sẽ thấy những đoạn đó tạo thành một hình bao dưới (lower envelope), một tập các đoạn thẳng chứa tất cả điểm cực tiểu cho mọi giá trị của $x$ (hình bao dưới được tô bằng màu xanh trong hình. Cái tên kĩ thuật bao lồi xuất phát từ việc đường bao trên tạo thành một đường lồi, từ đó thành bao lồi của một tập điểm.
Thêm một đường vào tập
Ta có thể thấy nếu ta có một tập đường thẳng đã được xác định sắp xếp, ta có thể dễ dàng trả lời bất kì truy vấn nào với độ phức tạp là $\mathcal{O}(\log{} M)$ với tìm kiếm nhị phân. Vậy nếu chúng ta tìm ra cách thêm một đường thẳng vào tính toán lại một cách hiệu quả là chúng ta đã có một thuật toán hoạt động ngon lành.
Giả sử chúng ta được xử lý tất cả đường thẳng trước khi làm các truy vấn thì chúng ta chỉ cần đơn giản sắp xếp các đường thẳng theo hệ số góc và thêm từng đường một vào. Sẽ có thể một số đường không quan trọng và sẽ bị bỏ đi. Chúng ta sẽ sử dụng cấu trúc dữ liệu Stack để cài đặt, bỏ từng đường thẳng vào stack và nếu đường nào không quan trọng sẽ bị bỏ ra ngoài đến khi chỉ còn một đường thẳng (đường thẳng cuối không thể bỏ)
Vậy làm sao để có thể xác định đường thẳng nào sẽ bị bỏ khỏi stack? Giả sử $l_1$, $l_2$ và $l_3$ là đường thẳng áp chót (gần cuối ) trên stack, đường thẳng cuối cùng trong stack và đường thẳng được thêm vào stack. Đoạn $l_2$ không quan trọng(không có giá trị cực tiểu ở điểm nào) khi và chỉ khi giao điểm của $l_1$ và $l_3$ nằm bên trái giao điểm của $l_1$ và $l_2$ (Đoạn mà $l_3$ nhận giá trị cực tiểu đã nằm đè lên đoạn của $l_2$). Giả sử rằng không có ba đường nào trùng hay song song với nhau (có thể giải quyết một cách đơn giản).
Phân tích thuật toán
Độ phức tạp bộ nhớ sẽ là $\mathcal{O}(M)$: chúng ta cần một danh sách lưu lại các đoạn thẳng, biểu diễn bởi hai số thực.
Độ phức tạp thời gian cho phần tiền xây dựng:
-
Để sắp xếp các đoạn thẳng theo tăng dần hệ số góc sẽ tốn $\mathcal{O}(M\log{M})$.
-
Duyệt qua các đường thẳng mỗi đường được cho vào stack và bỏ khỏi stack tối đa một lần vậy nên sẽ tốn $\mathcal{O}(M)$ cho bước này.
Vậy thời gian cho việc xây dựng sẽ là $\mathcal{O}(M\log{M})$. Với mỗi truy vấn dùng chặt nhị phân sẽ cho độ phúc tạp tốt nhất $\mathcal{O}(\log{} M)$.
Ví dụ 1: USACO Tháng 3 năm 2008 "Acquire"
Bài toán
Cho $N(N \le 50000)$ hình chữ nhật khác nhau về hình dạng, mục tiêu của bài toán là phải lấy được tất cả hình chữ nhật. Một tập hình chữ nhật có thể thu được với chi phí bằng tích của chiều dài dài nhất và chiều rộng dài nhất. Chúng ta cần phân hoạch tập các hình chữ nhật này một cách khôn khéo sao cho tổng chi phí có thể được tối thiểu hóa và tính chi phí này. Hình chữ nhật không thể được xoay (đổi chiều dài và chiều rộng).
Nhận xét 1: Tồn tại các hình chữ nhật không quan trọng
Giả sử tồn tại hai hình chữ nhật A và B mà mà cả chiều dài và chiều rộng của hình B đều bé hơn hình A thì ta có thể nói hình B là không quan trọng vì ta có thể để hình B chung với hình A từ đó chi phí của hình B không còn quan trọng. Sau khi đã loại hết tất cả hình không quan trọng đi và sắp xếp lại các hình theo chiều dài giảm dần thì chiều rộng các hình đã sắp xếp sẽ theo chiều tăng.
Nhận xét 2: Đoạn liên tiếp
Sau khi sắp xếp, ta có thể hình dung được rằng nếu chúng ta chọn hai hình chữ nhật ở vị trí $i$ và ở vị trí $j$ thì ta có thể chọn tất cả hình chữ nhật từ $i+1$ đến $j-1$ mà không tốn chi phí nào cả. Vậy ta có thể thấy rằng cách phân hoạch tối ưu là một cách phân dãy thành các đoạn liên tiếp và chi phí của một đoạn là bằng tích của chiều dài của hình chữ nhật đầu tiên và chiều rộng của hình chữ nhật cuối cùng.
Lời giải Quy Hoạch Động
Vậy bài toán trờ về bài toán phân dãy sao cho tổng chi phí của các dãy là tối ưu. Đây là một dạng bài quy hoạch động hay gặp và chúng ta có thể dễ dàng nghĩ ra thuật toán $\mathcal{O}(N^2)$ như mã giả phía dưới. (Giả sử các hình đã được sắp xếp và bỏ đi những hình chữ nhật không quan trọng)
input N
for i ∈ [1..N]
input rect[i].h
input rect[i].w
let cost[0] = 0
for i ∈ [1..N]
let cost[i] = ∞
for j ∈ [0..i-1]
cost[i] = min(cost[i],cost[j]+rect[i].h*rect[j+1].w)
print cost[N]Ở trên cost[k] lưu lại chi phí cực tiểu để lấy được k hình chữ nhật đầu tiên. Hiển nhiên, cost[0]=0. Để tính toán được cost[i] với i khác 0, ta có tính tổng chi phí để lấy được các tập trước và cộng nó với chi phí của tập cuối cùng(có chứa i). Chi phí của một tập có thể dễ dàng tính bằng cách lấy tích của chiều dài hình chữ nhật đầu tiên và chiều rộng của hình chữ nhật cuối cùng. Vậy ta có min(cost[i],cost[j]+rect[i].h*rect[j+1].w) với j là hình chữ nhật đầu tiên của tập cuối cùng. Với $N=50000$ thì thuật toán $\mathcal{O}(N^2)$ này là quá chậm.
Nhận xét 3: Sử dụng bao lồi
Với $m_j=rect[j+1].w, b_j=cost[j], x=rect[i].h$ với $rect[x].h$ là chiều rộng của hình chữ nhật $x$ và $rect[x].w$ là chiều dài của hình chữ nhật $x$. Vậy thì bài toán trờ về tìm hàm cực tiểu của $y=m_jx+b_j$ bằng cách tìm $j$ tối ưu. Nó giống hoàn toàn bài toán chúng ta đã đề cập ở trên. Giả sử ta đã hoàn thành việc cài đặt cấu trúc đã đề cập ở trên chúng ta có thể có mã giả ở dưới đây:
input N
for i ∈ [1..N]
input rect[i].h
input rect[i].w
let E = empty lower envelope structure
let cost[0] = 0
add the line y=mx+b to E, where m=rect[1].w and b=cost[0] //b is zero
for i ∈ [1..N]
cost[i] = E.query(rect[i].h)
if i<N
E.add(m=rect[i+1].w,b=cost[i])
print cost[N]Rõ ràng các đường thẳng đã được sắp xếp giảm dần về độ lớn của hệ số góc do chúng ta đã sắp xếp các chiều dài giảm dần. Do mỗi truy vấn có thể thực hiện trong thời gian $\mathcal{O}(\log{N})$, ta có thể dễ dàng thấy thời gian thực hiện của cả bài toán là $\mathcal{O}(N\log{N})$. Do các truy vấn của chúng ta cũng tăng dần (do chiều rộng đã được sắp xếp tăng tần) ta có thể thay thế việc chặt nhị phân bằng một con trỏ chạy song song với việc quy hoạch động đưa bước quy hoạch động còn $\mathcal{O}(N)$ nhưng tổng độ phức tạp vẫn là $\mathcal{O}(N\log{N})$ do chi phí sắp xếp. Vậy là ta đã giải quyết thành công bài toán sử dụng kĩ thuật bao lồi đầu tiên của chúng ta :D.
Ví dụ 2: APIO 2010 Commando
Bài toán
Bạn được cho:
- Một dãy có $N$ số nguyên dương ($1\le N \le 10^6$)
- Một hàm số bậc 2 với hệ số nguyên duong $f(x)= ax^2 + bx +c$, $a\lt0$. Mục tiêu cũng của bài toán là phân dãy này ra thành các đoạn liên tiếp sao tổng các hàm $f$ trên các dãy là lớn nhất ( giá trị của hàm $f$ lên dãy là $f(x)$ với $x$ là tổng dãy đó) . Tương tự như bài trên công thức quy hoạch động có thể dễ thấy công thức $\mathcal{O}(N^2)$.
Định nghĩa rằng:
sum(i,j) = x[i] + x[i+1] + ... + x[j]adjust(i,j) = a*sum(i,j)^2 + b*sum(i,j) + c
Ta có:
$dp(n) = max_{k=0}^{n-1}[dp(k)+adjust(k+1,n)]$
Mã giả:
dp[0] ← 0
for n ∈ [1..N]
for k ∈ [0..n-1]
dp[n] ← max(dp[n], dp[k] + adjust(k + 1 , n))Hãy thử biến đổi hàm "adjust" một tí nào. Định nghĩa $sum(1,x)$ là $\delta(x)$. Vậy với một số $k$ bất kì ta có thể viết là:
$dp(n)=dp(k)+a(\delta(n)-\delta(k))^2+b(\delta(n)-\delta(k))+c$ $dp(n)=dp(k)+a(\delta(n)^2+\delta(k)^2-2\delta(n)\delta(k))+b(\delta(n)-\delta(k))+c$ $dp(n)=(a\delta(n)^2 +b\delta(n) +c)+dp(k)-2a\delta(n)\delta(k)+a\delta(k)^2-b\delta(k)$
Nếu:
- $z=\delta(n)$
- $m=-2a\delta(k)$
- $p=dp(k)+a\delta(k)^2-b\delta(k)$
Ta có thể thấy $mz+p$ là đại lượng mà chúng ta muốn tối ưu hóa bằng cách chọn $k$. $dp(n)$ sẽ bằng đại lượng đó cộng thêm với $a\delta(n)+b\delta(n)+c$(độc lập so với k). Trong đó $z$ cũng độc lập với $k$, và $m$ và $p$ phụ thuộc vào k.
Ngược với bài "acquire" khi chúng ta phải tối thiểu hóa hàm quy hoạch động thì bài này chúng ta phải cực đại hóa nó. Chúng ta phải xây dựng một hình bao trên với các đường thẳng tăng dần về hệ số góc. Do đề bài đã cho $a\lt0$ hệ số góc của chúng ta tăng dần và luôn dương thỏa với điều kiện của cấu trúc chúng ta.
Do dễ thấy $\delta(n)>\delta(n-1)$, giống như bài "acquire" các truy vấn chúng ta cũng tăng dần theo thứ tự do vậy chúng ta có thể khơi tạo một biến chạy để chạy song song khi làm quy hoạch động (bỏ được phần chặt nhị phân).
Ví dụ 3: HARBINGERS (CEOI 2009)
Bài toán
Ngày xửa ngày xưa, có $N$ trị trấn kiểu trung cỏ trong khu tự trị Moldavian. Các trhị trấn này được đánh số từ $1$ đến $N$. Thị trấn $1$ là thủ đô. Các thị trấn được nối với nhau bằng $N-1$ con đường hai chiểu, mỗi con đường có độ dài được đo bằng km. Có duy nhất một tuyến đường nối giữa hai điểm bất kỳ (đồ thị các con đường là hình cây). Mỗi thị trấn không phải trung tâm có một người truyền tin.
Khi một thị trấn bị tấn công, tình hình chiến sự cần được bảo về thủ đô càng sớm càng tốt. Mội thông điệp được truyền bằng các người truyền tin. Mỗi người truyền tin được đặc trưng bởi lượng thời gian khởi động và vận tốc không đổi sau khi xuất phát.
Thông điệp luôn được truyền trên con đường ngắn nhất đến trung tâm. Ban đầu, thông tin chiến sự được đưa cho người truyền tin tại thị trấn bị tấn công. Từ thị trấn đó người truyền tin sẽ đi theo con đường về gần thủ đô hơn. Khi đến một thị trấn mới vừa đến. Lưu ý rằng khi chuyển sang người truyền tin mới thì người này cần một lượng thời gian để khởi động rồi mới đi chuyển tin. Như vậy, thông điệp sẽ được chuyển bằng một số người truyền tin trước khi đến thử đô.
Hãy xác định thời gian ít nhất cần chuyển tin từ các thị trấn về thủ đô.
Input
- Dòng đầu ghi số N.
- $N-1$ dòng tiếp theo, mỗi dòng ghi ba số $u$, $v$, và $d$ thể hiện một con đường nối từ $u$ đến $v$ với độ dài bằng $d$.
- $N-1$ dòng tiếp theo, dòng thứ $i$ gồm hai số $S_i$ và $V_i$ thể hiện thời gian cần để khởi động và số lượng phút để đi được $1$ km của người truyền tin ở thị trấn $i+1$.
Output
- Ghi $N-1$ số trên một dòng. Số thứ $i$ thể hiện thời gian ít nhất cần truyền tin từ thành phố $i+1$ về thủ đô.
Ví dụ
Input
5
1 2 20
2 3 12
2 4 1
4 5 3
26 9
1 10
500 2
2 30
Output
206 321 542 328Giới hạn
- $3 \le N \le 100 000$
- $0 \le S_i, V_i \le 10^9$
- Độ dài mỗi con đường không vượt quá $10000$
Lời giải
Thuật toán QHĐ
Gọi $F(i)$ là thời gian ít nhất để truyền tin từ thành phố thứ $i$ đến thủ đô, ta có công thức truy hồi:
$F(i) = min[ F(j) + dist(j, i) * V_i + S_i ]$
với $j$ là một nút trên đường từ thành phố $i$ đến thành phố $1$. Trong đó $dist(j, i)$ là khoảng cách giữa 2 thành phố $i$ và $j$, có thể tính trong $O(1)$ sử dụng mảng cộng dồn $D[]$ với $D[i]$ là khoảng cách từ thành phố $i$ tới thủ đô. Thuật toán này có thể dễ dàng cài đặt với độ phức tạp là $O(N^2)$.
Áp dụng bao lồi
Công thức truy hồi có thể viết lại thành
$F(i) = min[ F(j) - D_j * V_i + D_i * V_i + S_i ]$
Khi ta tính $F(i)$, thì giá trị $D_i*V_i + S_i$ là hằng số với mọi $j$, vì vậy
$F(i) = min[ F(j) - D_j * V_i ] + D_i * V_i + S_i$
Có thể thấy rằng ta cần tìm giá trị nhỏ nhất của hàm bậc nhất $y = -D_j*x + F(j)$ <dạng $y = ax + b$>. Với trường hợp cây là đường thẳng, ta có thể trực tiếp kỹ thuật đã trình bày ở phần trước. Trong trường hợp tổng quát, ta cần một cấu trúc dữ liệu cho phép xử lí hai thao tác:
- Khi DFS xuống một nút con, ta cần thêm một đường thẳng.
- Khi quá trình DFS tính $F[]$ cho gốc cây con đã hoàn tất, ta cần xóa một đường thẳng, trả cấu trúc dữ liệu về trạng thái ban đầu.
Các thao tác này có thể được thực hiện hiệu quả trong $O(logN)$. Cụ thể ta sẽ biểu diễn stack bằng một mảng cũng một biến $size$ (kích thước stack). Khi thêm một đường thẳng vào, ta sẽ tìm kiếm nhị phân vị trí mới của nó, rồi chỉnh sửa biến $size$ cho phù hợp, chú ý là sẽ có tối đa một đường thẳng bị ghi đè, nên ta chỉ cần lưu lại nó. Khi cần trả về trạng thái ban đầu, ta chỉ cần chỉnh sửa lại biến $size$ đồng thời ghi lại đường thẳng đã bị ghi đè trước đó. Để quản lí lịch sử các thao tác ta sử dụng một $vector$ lưu lại chúng. Độ phức tạp cho toàn bộ thuật toán là $O(NlogN)$.
#include <bits/stdc++.h>
#define X first
#define Y second
const int N = 100005;
const long long INF = (long long)1e18;
using namespace std;
typedef pair<int, int> Line;
struct operation {
int pos, top;
Line overwrite;
operation(int _p, int _t, Line _o) {
pos = _p; top = _t; overwrite = _o;
}
};
vector<operation> undoLst;
Line lines[N];
int n, top;
long long eval(Line line, long long x) {return line.X * x + line.Y;}
bool bad(Line a, Line b, Line c)
{return (double)(b.Y - a.Y) / (a.X - b.X) >= (double)(c.Y - a.Y) / (a.X - c.X);}
long long getMin(long long coord) {
int l = 0, r = top - 1; long long ans = eval(lines[l], coord);
while (l < r) {
int mid = l + r >> 1;
long long x = eval(lines[mid], coord);
long long y = eval(lines[mid + 1], coord);
if (x > y) l = mid + 1; else r = mid;
ans = min(ans, min(x, y));
}
return ans;
}
bool insertLine(Line newLine) {
int l = 1, r = top - 1, k = top;
while (l <= r) {
int mid = l + r >> 1;
if (bad(lines[mid - 1], lines[mid], newLine)) {
k = mid; r = mid - 1;
}
else l = mid + 1;
}
undoLst.push_back(operation(k, top, lines[k]));
top = k + 1;
lines[k] = newLine;
return 1;
}
void undo() {
operation ope = undoLst.back(); undoLst.pop_back();
top = ope.top; lines[ope.pos] = ope.overwrite;
}
long long f[N], S[N], V[N], d[N];
vector<Line> a[N];
void dfs(int u, int par) {
if (u > 1)
f[u] = getMin(V[u]) + S[u] + V[u] * d[u];
insertLine(make_pair(-d[u], f[u]));
for (vector<Line>::iterator it = a[u].begin(); it != a[u].end(); ++it) {
int v = it->X;
int uv = it->Y;
if (v == par) continue;
d[v] = d[u] + uv;
dfs(v, u);
}
undo();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> n;
int u, v, c;
for (int i = 1; i < n; ++i) {
cin >> u >> v >> c;
a[u].push_back(make_pair(v, c));
a[v].push_back(make_pair(u, c));
}
for (int i = 2; i <= n; ++i) cin >> S[i] >> V[i];
dfs(1, 0);
for (int i = 2; i <= n; ++i) cout << f[i] << ' ';
return 0;
}Biến thể động (Fully Dynamic Variant)
Kĩ thuật này có thể dễ dàng được thực hiện khi các đường thẳng được thêm trước tất cả các truy vấn hay các đường thẳng được thêm vào theo thứ tự giảm dần của hệ số góc. Hoặc với cấu trúc deque chúng ta cũng có thể thêm những đường thẳng có hệ số góc lớn hơn hết các đường thẳng đã có. Nhưng có những lúc sẽ có các bài toán khi chúng ta phải giải quyết các truy vấn và thêm đường thẳng lồng vào nhau với các hệ số góc ngẫu nhiên. Chúng ta không thể sắp xếp lại trước (do bị lồng vào truy vấn) và không thể sắp xếp lại với mỗi lần thêm đường thẳng (vậy sẽ cho ta một độ phức tạp tuyến tính với mỗi truy vấn).
Có tồn tại một cách để thêm các đường thẳng ngẫu nhiên vào trong độ phức tạp log. Chúng ta lưu các đoạn thẳng trong một cấu trúc có thứ tự động như std::set của C++. Mỗi đường thẳng chứa hệ số góc và giao điểm $y$ (sắp xếp theo hệ số góc trước rồi theo $y$) cùng với một biến $left$ thêm, $x$ nhỏ nhất sao cho đường thẳng này đạt cực tiểu trong tập các đường thẳng.
Sắp đường thẳng này vào vị trí đúng của nó và những đường bị loại sẽ là các đường liên tiếp kế bên nó. Chúng ta dùng các điều kiện tương tự trên để bỏ các đường thẳng bên trái và bên phải nó.
Để trả lời truy vấn, chúng ta dùng một set nữa dùng chính các biến ấy nhưng lại sắp xếp theo $left$. Vậy mỗi lần truy vấn ta có thể dễ dàng chặt nhị phân để tìm ra kết quả như đã nói ở trên.