Nhập môn Quy hoạch động

Nhập môn Quy hoạch động

Nguồn: Topcoder.

Có rất nhiều bài toán được áp dụng quy hoạch động (QHĐ) (Dynamic Programming). QHĐ là một trong những kĩ thuật quan trọng. Bài viết này sẽ giúp bạn hiểu được QHĐ thông qua các ví dụ cụ thể.

Note: Trong bài này có thể có nhiều phần bạn đã biết, bạn hoàn toàn có thể chuyển qua đọc phần khác.

Beginner

QHĐ là gì ?

QHĐ là kĩ thuật được được dùng khi có một công thức và một (hoặc một vài) trạng thái bắt đầu. Một bài toán được tính bởi các bài toán nhỏ hơn đã tìm ra trước đó. QHĐ có độ phức tạp đa thức nên sẽ chạy nhanh hơn quay lui và duyệt trâu.

Để hiểu rõ hơn hãy xem ví dụ sau:

Cho $N$ đồng xu và giá tiền của mỗi đồng ($V_0,V_1,…,V_{N-1}~$), và số $S$. Tìm số đồng xu nhỏ nhất để tổng giá trị của chúng bằng $S$ (số lượng đồng xu không giới hạn).

Bây giờ chúng ta sẽ xây dựng thuật giải:

Đầu tiên, cần tìm một trạng thái của bài toán.

Trạng thái là gì ?

Trạng thái là một trường hợp, một bài toán con của bài toán lớn.

Ví dụ, trạng thái trong bài này là số lượng xu nhỏ nhất để tổng bằng $i$, với $i \le S$. Để tìm ra trạng thái $i$, cần phải tìm tất cả các trạng thái $j$ mà $(j < i)$. Một khi đã tìm ra trạng thái $i$, ta có thể dễ dàng tìm ra trạng thái của $i+1$.

Làm thế nào để tìm được ?

Với mỗi $j$, $V_j \le i$, tìm số đồng xu nhỏ nhất để tổng bằng $i-V_j$. Giả sử nó bằng $m$. Nếu $m+1$ nhỏ hơn số lượng đồng xu hiện tại cho tổng $i$ thì ta cập nhập nó bằng $m+1$.

Sau đây là ví dụ: Cho các đồng xu với giá tiền 1, 3 và 5. Và $S$ = 11.

Đầu tiên, ta bắt đầu từ trạng thái 0, chúng ta có $f[0] = 0$. Xét đến tổng 1. Có duy nhất đồng xu 1 nhỏ hơn hoặc bằng tổng 1, nên ta có $f[1] = f[1-V_0] + 1 = f[0] + 1 = 1$. Xét đến tổng 2. Cũng giống như tổng trước, chỉ có 1 đổng xu $\le$ 2, có $f[2] = f[2-V_0] + 1 = f[1]+1 = 2$ Đến tổng 3. Lần này có 2 đồng xu $\le$ 3 là 1 và 3. - Nếu ta chọn đồng 1, ta có $f[3] = f[3-V_0] + 1 = f[2] + 1 = 3$ - Nếu ta chọn đồng 3, ta có $f[3] = f[3-V_1] + 1 = f[0] + 1 = 1$ Rõ ràng là 1 $\le$ 3 nên ta chọn đồng 3 và $f[3] = 1$ Xét tiếp đến tổng 4, rồi đến 11 bằng cách như trên.

Mã giả:

Gán Min[i] bằng dương vô cùng với mọi i
Min[0]=0

For i = 1 to S
For j = 0 to N - 1
   If (Vj<=i AND Min[i-Vj]+1<Min[i])
Then Min[i]=Min[i-Vj]+1
Output Min[S]

Đây là lời giải cho tất cả các tổng:

Tổng Lượng xu nhỏ nhất Xu được chọn
(tổng còn lại)
0 0 -
1 1 1 (0)
2 2 1 (1)
3 1 3 (0)
4 2 1 (3)
5 1 5 (0)
6 2 3 (3)
7 3 1 (6)
8 2 3 (5)
9 3 1 (8)
10 2 5 (5)
11 3 1 (10)

Vậy là chúng ta đã tìm được lời giải cho 3 đồng xu tổng bằng 11. Dựa vào bảng trên, ta có thể truy vết lại được những đồng xu nào được chọn để tối ưu bài toán. Bài QHĐ trên còn có một cách tiếp cận khác nữa. Lần này, ta sẽ không tính liên tiếp các tổng. Bắt đầu từ trạng thái 0. Thử nhét đồng xu thứ 1 vào các tổng đã tính. Nếu như tổng $t$ có số đồng xu ít hơn số đồng xu hiện tại thì tiến hành cập nhật. Rồi tiếp tục thử với đồng thứ 2, 3 cho đến khi thử hết các đồng. Ví dụ, nhét đồng 1 (giá trị 1) vào tổng 0 ta có tổng 1. Vì ta chưa tính tổng 1 nên $S[1] = 1$. Nhét đồng 1 vào tổng 1 ta có $S[2] = 2$. Tiếp tục làm như vậy với các tổng còn lại. Sau đồng 1, ta nhét đồng 2(giá trị 3) vào tổng 0 ta được 1, mà $S[3] = 3 > 1$, ta cập nhật $S[3] = 1$. Tiếp tục nhét đồng 2 vào các tổng còn lại, cũng nhứ thử nhét các đồng xu khác.

#Elementary

Bây giờ, chúng ta cùng đến một khái niệm mới, công thức truy hồi (recurrent relation), mối liên hệ giữa những trạng thái.

Ví dụ: Cho một dãy N số - $A[1], A[2], …, A[N]$. Tìm dãy con không giảm dài nhất.

Ta quy định trạng thái $S[i]$ là dãy con không giảm dài nhất kết thúc tại $A[i]$. Với $i>1$ và $j<i$, tính được $i$ khi tồn tại $A[j] \le A[i]$ (vì đây là dãy không giảm). Khi đó $S[i] = Max(S[i], S[j] + 1)$. Tiếp tục tính như vậy cho đến khi đến được trạng thái $S[N]$.

Hãy xem bảng sau với dãy: 5, 3, 4, 8, 6, 7:

I Độ dài dãy con
không giảm dài nhất
của i số đầu tiên		 Vị trí của kí tự cuối
trong dãy
1 1 1
2 1 2
3 2 2
4 3 3
5 3 3
6 4 5

Bài luyện tập: Cho đồ thị vô hướng $G$ có $N$ đỉnh ($N \le 1000$) và các cạnh có trọng số dương. Tìm đường đi ngắn nhất từ đỉnh 1 đến đỉnh $N$ hoặc thông báo không tồn tại đường đi. Gợi ý: Tại mỗi bước, chọn ra trong số các đỉnh chưa thăm mà có đường đi từ 1, chọn ra đỉnh có đường đi ngắn nhất.

Các bài ví dụ khác:

Intermediate

Tới đây bạn sẽ được làm quen với QHĐ 2 chiều.

Bài toán: Cho một bảng $M * N$, mỗi ô có một lượng táo. Bắt đầu từ ô trái trên, mỗi bước có thể đi sang phải hoặc xuống dưới. Bạn có thể ăn được nhiều nhất bao nhiêu quả táo ?

Cách giải bài này cũng tương tự như những bài trước.

Đầu tiên là phải xác định trạng thái là gì. Ở mỗi ô có nhiều nhất 2 cách có thể tới được ô đó, từ ô bên trái và ô phía trên. Do vậy, để tìm trạng thái hiện tại, ta phải tính trước các ô có thể đến được nó.

Ta có công thức truy hồi sau: $S[i][j]=A[i][j] + max(S[i-1][j], if$ $ i>0 ; S[i][j-1], if$ $j>0)$ (trong đó, $i$ là hàng, $j$ là cột, $A[i][j]$ là số táo ở ô $i,j$) $S[i][j]$ có thể được tính từ trái sang phải, từ trên xuống dưới, hoặc từ trên xuống, từ trái sang.

Mã giả:

For i = 0 to N - 1
   For j = 0 to M - 1
   S[i][j] = A[i][j] +
      max(S[i][j-1], if j>0 ; S[i-1][j], if i>0 ; 0)

Output S[n-1][m-1]

Ví dụ khác:

#Upper-Intermediate

Phần này sẽ giới thiệu với bạn những bài toán cùng với một số điều kiện.

Đây là một ví dụ cụ thể:

Cho đồ thị vô hướng $G$ có trọng số dương và $N$ đỉnh.

Ban đầu bạn có số tiền là $M$. Để đi qua đỉnh $i$, bạn phải trả số tiền là $S[i]$. Và đương nhiên, nếu không đủ tiền thì bạn không đi được. Tìm đường đi ngắn nhất từ 1 tới $N$ thỏa mãn tiêu chí trên. Nếu có nhiều đường ngắn nhất, in ra đường với chi phí nhỏ nhất. Giới hạn: $1<N \le 100 $; $0 \le M \le 100$; $0 \le S[i] \le 100$.

Có thể dễ dàng thấy đây là một bài Dijkstra cơ bản, tuy nhiên chỉ khác ở chỗ nó có thêm một điều kiện. Trong bài toán Dijkstra cơ bản ta có $Min[i]$ , là độ dài đường đi ngắn nhất từ 1 tới $i$. Còn ở đây, chúng ta cần phải quan tâm đến số tiền còn lại. Do đó chúng ta có thể mở rộng mảng này thành $Min[i][j]$ , là độ dài đường đi ngắn nhất tới $i$, và còn lại số tiền là $j$. Bằng cách này bài toán đã được đưa về bài toán Dijkstra quen thuộc. Tại mỗi bước ta tìm trạng thái $(i,j)$ có quãng đường ngắn nhất, đánh dấu là đã thăm rồi update cho các trạng thái cạnh nó. Đáp án sẽ là $Min[N][j]$ có giá trị nhỏ nhất (và $j$ lớn nhất trong số các $Min[N][j]$ có cùng giá trị).

Mã giả:

Gán mọi(i,j) là chưa thăm
Gán Min[i][j] bằng dương vô cùng với mọi (i,j)

Min[0][M]=0

While(TRUE)

    Trong số những trạng thái chưa thăm (i,j) tìm cái có Min[i][j]
    nhỏ nhất. Giải sử nó là (k,l).

    Nếu không tìm được (k,l) nào mà Min[k][l] nhỏ hơn dương vô cùng - thoát vòng lặp.

    Đánh dấu (k,l) đã thăm

    For All Neighbors p of Vertex k.
       If (l-S[p]>=0 AND
        Min[p][l-S[p]]>Min[k][l]+Dist[k][p])
          Then Min[p][l-S[p]]=Min[k][l]+Dist[k][p]
       i.e.
    Nếu tại (i,j) có đủ tiền để đi qua p (l-S[p] là số tiền còn lại sau khi đi qua p), và đường đi ngắn nhất của (p,l-S[p]) lớn hơn [đường đi ngắn nhất tới (k,l)] + [khoảng cách từ k tới p)],
    thì gán (i,j) bằn tổng này.
    End For

End While

Tìm số nhỏ nhất trong các Min[N-1][j] (for all j, 0<=j<=M);
Nếu có nhiều hơn một trạng thái, lấy trạng thái nào có j lớn nhất. Nếu không có (N-1,j) nào nhỏ hơn dương vô cùng - không tồn tại đường đi.

Các bài luyện tập:

Advanced

Những bài sau đây sẽ cần một chút kĩ năng phân tích để có thể tối ưu chúng thành bài QHĐ.

Problem StarAdventure – SRM 208 Div 1:

Cho ma trận M hàng, N cột ($N * M$). Mỗi ô có một lượng táo. Bạn đang ở ô góc trái trên. Bạn chỉ có thể đi xuống hoặc sang phải. Bạn cần tới ô góc phải dưới. Rồi quay lại ô trái trên bằng cách lên hoặc sang trái. Cuối cùng, bạn quay lại ô phải dưới. Tìm số táo nhiều nhất mà bạn có thể ăn được. Khi đi qua một ô, toàn bộ táo của ô đấy sẽ bị ăn hết.

Giới hạn: $1 < N, M \le 50$ mỗi ô có từ 0 đến 1000 quả táo.

Đọc đến đây, hẳn bạn sẽ thấy cái đề này quen quen, nó chính là bài mở rộng của bài toán phần Intermediate. Ta có thể thử đưa bài toán này về thành bài toán trên. Để ý thấy đường đi từ ô góc phải dưới lên trái trên cũng có thể coi là một đường đi từ góc trái trên xuống. Như vậy, chúng ta phải xử lý bài toán với 3 đường đi từ trái trên xuống. Gọi 3 đường này là trái, giữa và phải. Khi 2 đường giao nhau (như hình dưới):

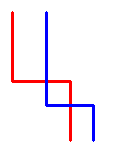
enter image description here

thì nó cũng tương đương với hình sau:

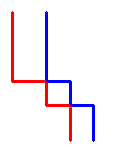
enter image description here

Bằng cách này, chúng ta đã có một cái nhìn khác về bài toán. Các đường này sẽ không giao nhau (trừ ô góc trái trên và phải dưới). Với mỗi hàng y (không phải hàng đầu và cuối), tọa độ x ở mỗi đường sẽ là ($x1[y]$ , $x2[y]$ và $x3[y]$ ) : $x1[y] < x2[y] < x3[y]$ . Ta xét hàng thứ y. Giả sử, ta xét $x1[y-1]$ , $x2[y-1]$ and $x3[y-1]$ và số táo hiện giờ thu được là nhiều nhất. Từ đó ta có thể tối ưu cho hàng $y$. Chúng ta cần tìm cách chuyển trạng thái. Gọi $Max[i][j][k]$ là lượng táo nhiều nhất thu được đến hàng $y-1$ với 3 đường đang dừng ở cột $i$, $j$, và $k$. Với hàng $y$, thêm vào $Max[i][j][k]$ số lượng táo ở các ô $(y,i)$ , $(y,j)$ and $(y,k)$. Vì chúng ta đang đi xuống. Sau đó, chúng ta xét đến những đường có thể sang phải. Để tránh việc giao nhau, ta xét lần lượt các bước ở trái, phải rồi giữa.

Bài luyện tập thêm:

Note: Khi gặp một bài toán, hãy để ý xem nó có được giải trong thời gian đa thức không. Nếu có, thử xác định trạng thái của nó, cách chuyển trạng thái, và nếu không chuyển được trạng thái, hãy thử tối ưu nó về một bài QHĐ (như ví dụ ở trên).

Những bài đã đề cập ở trên: