Bài toán RMQ và bài toán LCA

Bài toán RMQ và bài toán LCA

Nguồn: Topcoder

Table of Contents

Trong bài viết này, tác giả sẽ giới thiệu với bạn 2 bài toán cơ bản: Bài toán RMQ và bài toán LCA, cũng như mối liên hệ giữa 2 bài toán này.

Các định nghĩa

Gỉa sử thuật toán có thời gian tiền xử lý là $f(n)$ và thời gian trả lời 1 truy vấn là $g(n)$. Ta ký hiệu độ phức tạp tổng quát của thuật toán là $< f(n),g(n) >$.

Trong bài này, khi viết $\log{N}$, chúng ta hiểu là log cơ số 2 của $N$.

Bài toán Range Minimum Query (RMQ)

Cho mảng $A[0,N-1]$. Bạn cần trả lời $Q$ truy vấn. Mỗi truy vấn gồm 2 số $i$, $j$ và bạn cần đưa ra vị trí của phần tử có giá trị nhỏ nhất trong đoạn từ $i$ đến $j$ của mảng $A$, ký hiệu là $RMQ_A(i,j)$.

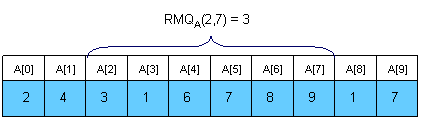
Bài toán Lowest Common Ancestor (LCA)

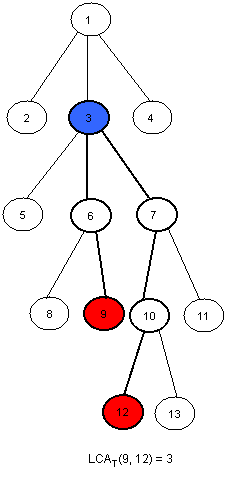
Cho cây có gốc $T$. Bạn cần trả lời $Q$ truy vấn. Mỗi truy vấn gồm 2 số $u$, $v$ và bạn cần tìm nút xa gốc nhất mà là tổ tiên của cả 2 nút $u$ và $v$, ký hiệu là $LCA_T(u,v)$.

Bài toán RMQ

Thuật toán $< O(1), O(N) >$

Thuật toán hiển nhiên nhất cho bài RMQ là ta không cần tiền xử lý gì cả. Với mỗi truy vấn, ta xét lần lượt từng phần tử từ $i$ đến $j$ để tìm phần tử nhỏ nhất. Hiển nhiên, độ phức tạp thuật toán này là $< O(1), O(N) >$.

Thuật toán $< O(N^2),O(1) >$

Lưu giá trị của $RMQ_A(i,j)$ trong một bảng $M[0,N-1][0,N-1]$.

Thuật toán sẽ có độ phức tạp $< O(N^3),O(1) >$. Tuy nhiên ta có thể sử dụng quy hoạch động để giảm độ phức tạp xuống $< O(N^2),O(1) >$ như sau:

    for i = 0 .. N-1
        M[i][i] = i;

    for i = 0 .. N-1
        for j = i+1 .. N-1
            if (A[M[i][j - 1]] < A[j])
                M[i][j] = M[i][j - 1];
            else
                M[i][j] = j;

Có thể thấy thuật toán này khá chậm và tốn bộ nhớ $O(N^2)$ nên sẽ không hữu ích với những dữ liệu lớn hơn.

Thuật toán $< O(N),O(\sqrt N) >$

Ta có thể chia mảng thành $\sqrt N$ phần. Ta sử dụng một mảng $M[0, \sqrt N]$ để lưu giá trị mỗi phần. $M$ có thể dễ dàng tính được trong $O(N)$:

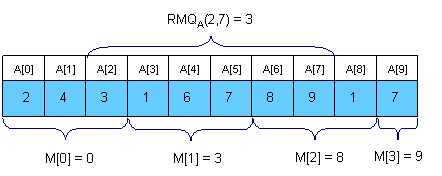
Để tính $RMQ_A(i,j)$, chúng ta xét giá trị $M$ của $\sqrt N$ phần nằm trong đoạn $[i,j]$, và những phần tử ở đầu và cuối đoạn $[i,j]$ là giao giữa các phần. Ví dụ, để tính $RMQ_A(2,7)$ ta chỉ cần so sánh $A[2]$, $A[M[1]]$, $A[6]$ và $A[7]$.

Dễ thấy thuật toán không sử dụng quá $3\sqrt N$ phép toán cho mỗi truy vấn.

Sparse Table (ST)

Đây là một hướng tiếp cận tốt hơn để tiền xử lý $RMQ$ cho các đoạn con có độ dài $2^k$, sử dụng quy hoạch động.

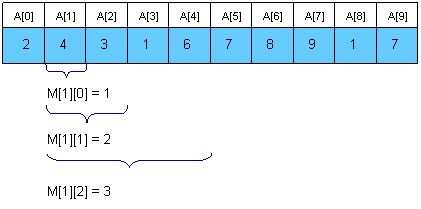
Ta sử dụng mảng $M[0,N-1][0,logN]$ với $M[i][j]$ là chỉ số của phần tử có giá trị nhỏ nhất trong đoạn có độ dài $2^j$ và bắt đầu ở $i$. Ví dụ:

Để tính $M[i][j]$, ta xét $M$ của 2 nửa đầu và nửa cuối của đoạn, mỗi phần sẽ có độ dài $2^{j-1}$:

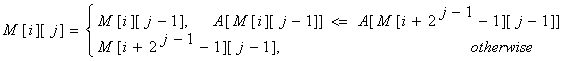
void process2(int M[MAXN][LOGMAXN], int A[MAXN], int N)
{
  int i, j;

  // Khởi tạo M với các khoảng độ dài 1
  for (i = 0; i < N; i++)
    M[i][0] = i;

  // Tính M với các khoảng dài 2^j
  for (j = 1; 1 << j <= N; j++)
    for (i = 0; i + (1 << j) - 1 < N; i++)
      if (A[M[i][j - 1]] < A[M[i + (1 << (j - 1))][j - 1]])
        M[i][j] = M[i][j - 1];
      else
        M[i][j] = M[i + (1 << (j - 1))][j - 1];
}

Để tính $RMQ_A(i,j)$ ta dựa vào 2 đoạn con độ dài $2^k$ phủ hết $[i,j]$, với $k= \lfloor log(j-i+1) \rfloor$:

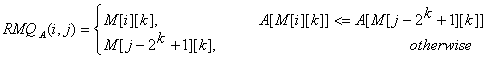
Độ phức tạp tổng quát của thuật toán này là $< O(NlogN),O(1) >$

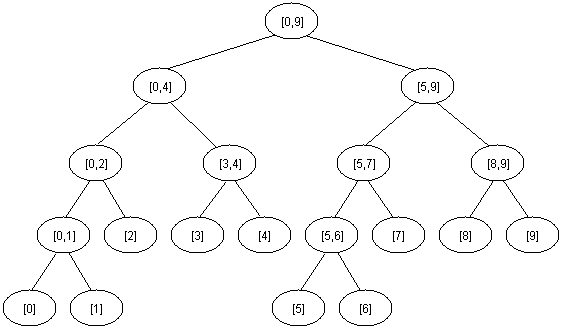
Cây phân đoạn (segment tree, interval tree, range tree)

Ta biểu diễn cây bằng một mảng $M[1,2*2^{[logN]+1}]$ với $M[i]$ là vị trí có giá trị nhỏ nhất trong đoạn mà nút $i$ quản lý.

Khởi tạo:

void initialize(intnode, int b, int e, int M[MAXIND], int A[MAXN], int N)
{
  if (b == e)
    M[node] = b;
  else
  {
    // Khởi tạo nút con trái và nút con phải
    initialize(2 * node, b, (b + e) / 2, M, A, N);
    initialize(2 * node + 1, (b + e) / 2 + 1, e, M, A, N);

    // Tính giá trị nhỏ nhất dựa trên 2 nút con
    if (A[M[2 * node]] <= A[M[2 * node + 1]])
      M[node] = M[2 * node];
    else
      M[node] = M[2 * node + 1];
  }
}

Truy vấn:

int query(int node, int b, int e, int M[MAXIND], int A[MAXN], int i, int j)
{
  int p1, p2;

  // Đoạn cần tính không giao với đoạn của nút hiện tại
  // --> return -1
  if (i > e || j < b)
    return -1;

  // Đoạn cần tính nằm trong hoàn toàn trong đoạn của nút hiện tại
  // --> return M[node]
  if (b >= i && e <= j)
    return M[node];

  // Tìm giá trị nhỏ nhất trong 2 cây con trái và cây con phải
  p1 = query(2 * node, b, (b + e) / 2, M, A, i, j);
  p2 = query(2 * node + 1, (b + e) / 2 + 1, e, M, A, i, j);

  // Tìm giá trị nhỏ nhất trong các cây con
  if (p1 == -1)
    return M[node] = p2;
  if (p2 == -1)
    return M[node] = p1;
  if (A[p1] <= A[p2])
    return M[node] = p1;
  return M[node] = p2;
}

Mỗi truy vấn sẽ được thực hiện trong $O(logN)$ và thuật toán có độ phức tạp tổng quát là $< O(N),O(logN) >$

Bài toán LCA

Thuật toán $< O(N), O(N) >$

Thuật toán đơn giản nhất như sau:

  • Đặt $h(u)$ là độ cao của đỉnh $u$.
  • Để trả lời truy vấn $u$, $v$. Không làm mất tính tổng quát, giả sử $h(u) > h(v)$.
    • Ta đi từ $u$ đến $u'$, với $u'$ là tổ tiên của $u$ và $h(u') = h(v)$.
    • Ta đồng thời đi từ $u$ và $v$ lên cha của nó, đến khi 2 đỉnh này trùng nhau (lúc đó cả 2 đỉnh đều ở LCA).

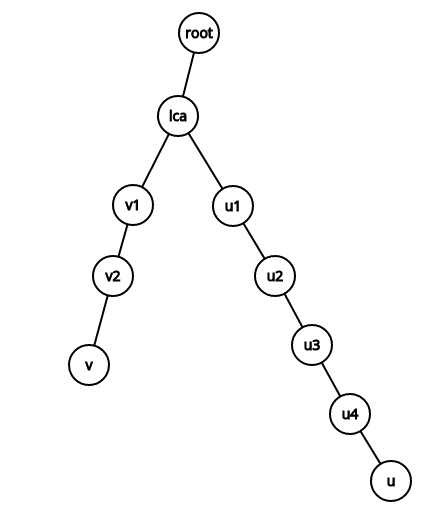
Ví dụ:

  • Ta cần tìm LCA của $u$ và $v$. Ban đầu $h(u) > h(v)$.
  • Ta đi từ $u$ đến tổ tiên của $u$ mà có $h(u') = h(v)$: Đi từ $u$ lên $u4$ lên $u3$.
  • Sau đó đồng thời đi từ $u$ và $v$ lên cha của nó đến khi 2 đỉnh bằng nhau:
    • $u = u2, v = v2$
    • $u = u1, v = v1$
    • $u = v = lca$
function LCA(u, v):
  if h(u) < h(v):
    swap(u, v)

  while h(u) > h(v):
    u = parent(u)

  while u != v:
    u = parent(u)
    v = parent(v)

  return u

Thuật toán $< O(N),O(\sqrt N) >$

Ý tưởng chia input thành các phần bằng nhau như trong bài toán $RMQ$ cũng có thể được sử dụng với $LCA$. Chúng ta sẽ chia cây thành $\sqrt H$ phần, với $H$ là chiều cao cây. Phần đầu bao gồm các tầng từ $0$ đến $\sqrt H-1$, phần 2 sẽ gồm các tầng từ $\sqrt H$ đến $2\sqrt H-1$,…:

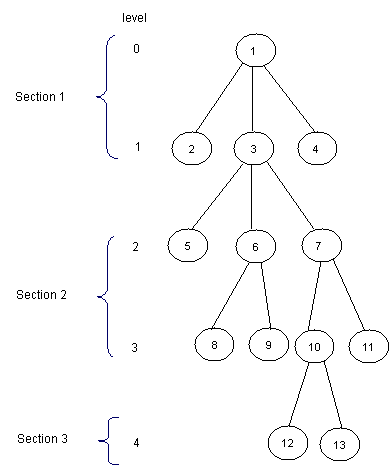
Giờ với mỗi nút chúng ta có thể biết được nút tổ tiên ở phần ngay trên nó. Ta sẽ tính giá trị này sử dụng mảng $P[1,MAXN]$:

Ta có thể tính $P$ bằng DFS ($T[i]$ là cha của $i$, $nr=\sqrt H$ và $L[i]$ là tầng của nút $i$)

void dfs(int node, int T[MAXN], int N, int P[MAXN], int L[MAXN], int nr)  {
      int k;

  // Nếu nút ở phần đầu tiên, thì P[node] = 1
  // Nếu nút ở đầu của 1 phần, thì P[node] = T[node]
  // Trường hợp còn lại, P[node] = P[T[node]]
  if (L[node] < nr)
    P[node] = 1;
  else
    if(!(L[node] % nr))
      P[node] = T[node];
    else
      P[node] = P[T[node]];

  // DFS xuống các con
  for each son k of node
    dfs(k, T, N, P, L, nr);
}

Truy vấn:

int LCA(int T[MAXN], int P[MAXN], int L[MAXN], int x, int y)
{
  // Nếu còn nút ở phần tiếp theo không phải là tổ tiên của cả x và y,
  // ta nhảy lên phần tiếp theo. Đoạn này cũng tương tự như thuật toán
  // <O(1), O(N)> nhưng thay vì nhảy từng nút, ta nhảy từng đoạn.
  while (P[x] != P[y])
    if (L[x] > L[y])
      x = P[x];
    else
      y = P[y];

  // Giờ x và y ở cùng phần. Ta tìm LCA giống như thuật <O(1), O(N)>
  while (x != y)
    if (L[x] > L[y])
      x = T[x];
    else
      y = T[y];
    return x;
}

Hàm này sử dụng tối đa $2\sqrt H$ phép toán. Với cách tiếp cận này chúng ta có thuật toán $< O(N),O(\sqrt H) >$, trong trường hợp tệ nhất thì $N=H$ nên độ phức tạp tổng quát của thuật toán là $< O(N),O(\sqrt N) >$.

Thuật toán $< O(NlogN),O(logN) >$

Ứng dụng Sparse Table chúng ta có một thuật toán nhanh hơn. Đầu tiên chúng ta tính một bảng $P[1,N][1,logN]$ với $P[i][j]$ là tổ tiên thứ $2^j$ của $i$:

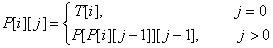
Code:

void process3(int N, int T[MAXN], int P[MAXN][LOGMAXN])
{
  int i, j;

  // Khởi tạo
  for (i = 0; i < N; i++)
    for (j = 0; 1 << j < N; j++)
      P[i][j] = -1;

  // Khởi tạo cha thứ 2^0 = 1 của mỗi nút
  for (i = 0; i < N; i++)
    P[i][0] = T[i];

  // Quy hoạch động
  for (j = 1; 1 << j < N; j++)
    for (i = 0; i < N; i++)
      if (P[i][j - 1] != -1)
        P[i][j] = P[P[i][j - 1]][j - 1];
}

Bước khởi tạo này tốn $O(NlogN)$ bộ nhớ lẫn thời gian.

Cách tìm LCA giống hệt như thuật toán $<O(1), O(N)>$, nhưng để tăng tốc, thay vì nhảy lên cha ở mỗi bước, thì ta dùng mảng $P$ để nhảy, từ đó thu được độ phức tạp $O(logN)$ cho mỗi bước. Cụ thể:

  • Gọi $h(u)$ là độ cao của nút $u$. Để tính $LCA(u, v)$, giả sử $h(u) > h(v)$, đầu tiên ta tìm $u'$ là tổ tiên của $u$ và có $h(u') = h(v)$:
    • Rõ ràng, ta cần nhảy từ $u$ lên cha thứ $h(u) - h(v)$. Ta chuyển $h(u) - h(v)$ sang hệ 2. Duyệt $j$ từ $log(h(u))$ xuống $0$, nếu tổ tiên thứ $2^j$ của $u$ không cao hơn $v$ thì ta cho $p$ nhảy lên tổ tiên thứ $2^j$ của nó.
  • Sau khi $u$ và $v$ đã ở cùng tầng, ta sẽ tính $LCA(u, v)$: cũng như trên, ta sẽ duyệt $j$ từ $log(h(u))$ xuống $0$, nếu tổ tiên thứ $2^j$ của $u$ và $v$ khác nhau thì chắc chắn $LCA(u, v)$ sẽ ở cao hơn, khi đó ta sẽ cho cả $u$ và $v$ nhảy lên tổ tiên thứ $2^j$ của nó. Cuối cùng thì $u$ và $v$ sẽ có cùng cha, vậy nên khi đó $LCA(u, v) = T[u] = T[v]$.

Code:


function LCA(N, P[MAXN][MAXLOGN], T[MAXN], h[MAXN], u, v):
  if h(u) < h(v):
    // Đổi u và v
    swap(u, v)

  log = log2( h(u) )

  // Tìm tổ tiên u' của u sao cho h(u') = h(v)

  for i = log .. 0:
    if h(u) - 2^i >= h(v):
      u = P[u][i]

  if u == v:
    return u

  // Tính LCA(u, v):
  for i = log .. 0:
    if P[u][i] != -1 and P[u][i] != P[v][i]:
      u = P[u][i]
      v = P[v][i]

  return T[u];

Mỗi lần gọi hàm này chỉ tốn tối đa $2logH$ phép toán. Trong trường hợp tệ nhất thì $H=N$ nên độ phức tạp tổng quát của thuật toán này là $< O(NlogN),O(logN) >$.

Bài toán LCA còn có nhiều cách giải thú vị khác. Các bạn có thể tham khảo thêm trong bài viết này.

Từ LCA đến RMQ

Ta có thể biến đổi bài toán LCA thành bài toán RMQ trong thời gian tuyến tính, do đó mà mọi thuật toán để giải bài toán RMQ đều có thể sử dụng để giải bài toán LCA. Hãy cùng xét ví dụ sau:

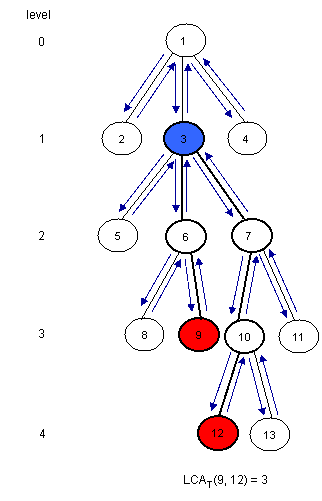
Để ý rằng $LCA_T(u,v)$ là nút gần gốc nhất xuất hiện giữa lúc thăm $u$ và $v$ trong phép duyệt DFS. Vì thế ta có thể xét tất cả các phần tử giữa các cặp chỉ số bất kì của $u$ và $v$ trong dãy Euler Tour và tìm nút cao nhất. Ta xây dựng 3 mảng:

  • $E[1,2*N-1]$: dãy thứ tự thăm của các nút trên đường đi Euler, $E[i]$ là nút được thăm thứ $i$ trên đường đi.

  • $L[1,2*N-1]$: tầng của các nút, $L[i]$ là tầng của nút $E[i]$

  • $H[1,N]$: $H[i]$ là vị trí xuất hiện đầu tiên của nút $i$ trên Euler Tour

Gỉa sử $H[u]<H[v]$. Dễ thấy việc cần làm lúc này là tìm nút có $L$ nhỏ nhất trên $E[H[u]..H[v]]$. Do đó $LCA_T(u,v)=E[RMQ_L(H[u],H[v]))]$. Ví dụ:

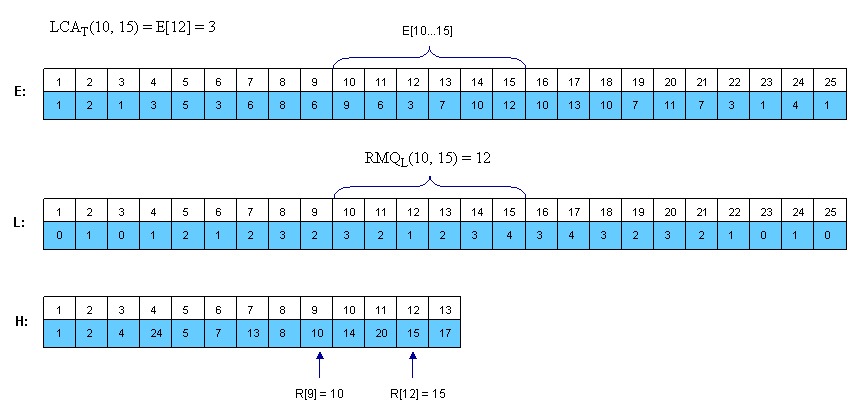
Cũng dễ thấy là mỗi 2 phần tử liên tiếp trong $L$ đều hơn kém nhau đúng 1 đơn vị.

Từ RMQ đến LCA

Một cây Cartesian của một dãy $A[0,N-1]$ là một cây nhị phân $C(A)$ có gốc là phần tử nhỏ nhất trong $A$ và có vị trí $i$. Cây con trái của $C(A)$ là cây Cartesian của $A[0,i-1]$ nếu $i>0$, ngược lại thì không có. Cây con phải của $C(A)$ là cây Cartesian của $A[i+1,N-1]$.

Dễ thấy rằng $RMQ_A(i,j)=LCA_C(i,j)$.

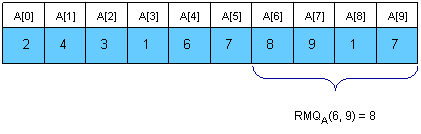
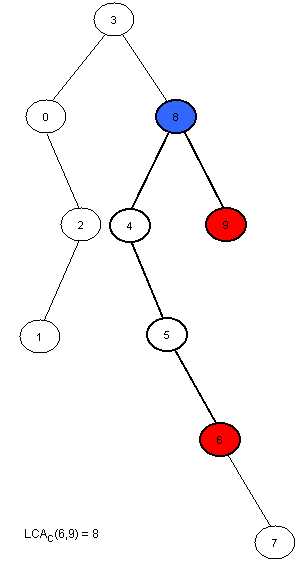
Bây giờ việc cần làm chỉ còn là tính $C(A)$ trong thời gian tuyến tính. Chúng ta sẽ sử dụng một cái stack.

  • Ban đầu stack rỗng. Ta lần lượt đẩy các phần tử của $A$ vào stack.

  • Tại bước thứ $i$, $A[i]$ sẽ được đẩy vào ngay cạnh phần tử cuối cùng không lớn hơn $A[i]$ trong stack, các phần tử lớn hơn $A[i]$ bị loại khỏi stack. Phần tử trong stack ở vị trí của $A[i]$ trước khi chèn $A[i]$ vào sẽ là con trái của $i$, còn $i$ sẽ là con phải của phần tử trước nó trong stack. Ở mỗi bước thì phần tử đầu tiên trong stack sẽ là gốc của cây Cartesian.

Ví dụ đối với cây ở trên:

Bước Stack Sự hình thành cây
0 0 0 là nút duy nhất trong cây
1 0 1 1 được đẩy vào cuối stack. Giờ 1 là con phải của 0
2 0 2 A[2] < A[1]. Lúc này 2 là con phải của 0 và con trái của 2 là 1
3 3 A[3] hiện đang là phần tử nhỏ nhất cho nên mọi phần tử của stack bị lấy ra ra và 3 trở thành gốc cây. Con trái của 3 là 0
4 3 4 4 được thêm vào cạnh 3 và con phải của 3 là 4
5 3 4 5 5 được thêm vào cạnh 4, con phải của 4 là 5
6 3 4 5 6 6 được thêm vào cạnh 5, con phải của 5 là 6
7 3 4 5 6 7 7 được thêm vào cạnh 6, con phải của 6 là 7
8 3 8 8 được thêm vào cạnh 3, các phần tử lớn hơn bị loại bỏ. 8 giờ là con phải của 3 và con trái của 8 là 4
9 3 8 9 9 được thêm vào cạnh 8, con phải của 8 là 9

Vì mỗi phần tử của $A$ đều chỉ đẩy vào và lấy ra 1 lần nên độ phức tạp thuật toán là $O(N)$.

void computeTree(int A[MAXN], int N, int T[MAXN])  {
      int st[MAXN], i, k, top = -1;

  // Bắt đầu với stack rỗng
  // Ở bước thứ i ta đẩy i và stack
  for (i = 0; i < N; i++)
  {
    //Tìm vị trí của phần tử đầu tiên nhỏ hơn hoặc bằng A[i] trong stack
    k = top;
    while (k >= 0 && A[st[k]] > A[i])
      k--;

    // Chỉnh sửa cây theo mô tả ở trên
    if (k != -1)
      T[i] = st[k];
    if (k < top)
      T[st[k + 1]] = i;

    // Đẩy i vào stack rồi xóa các phần tử lớn hơn A[i]
    st[++k] = i;
    top = k;
  }
  // Phần tử đầu tiên trong stack là gốc cây nên nó không có cha
  T[st[0]] = -1;
}

Thuật toán $< O(N),O(1) >$ cho bài toán RMQ thu hẹp

Bài toán $RMQ$ phát sinh khi giải bài toán LCA chỉ là trường hợp đặc biệt của bài toán RMQ tổng quát, do ta có điều kiện $|A[i]-A[i-1]|=1$ với mọi $i\in[1,N-1]$ (lý do là 2 phần tử liên tiếp có quan hệ cha con với nhau). Ta gọi bài toán $RMQ$ này là bài toán RMQ thu hẹp. Trong 1 số tài liệu còn được gọi là bài toán $\pm 1 RMQ$. Trong mục này, ta sẽ nghiên cứu một thuật toán có độ phức tạp tốt hơn cho bài toán RMQ thu hẹp.

Hãy biến đổi $A$ thành một dãy nhị phân có $N-1$ phần tử, với $B[i]=A[i]-A[i-1]$. Như vậy $A[i]=A[0]+B[1]+..+B[i]$ và $B[i]$ chỉ nhận giá trị $1$ hoặc $-1$.

Chúng ta chia $A$ thành các block kích thước $l=[log(N)/2]$. Gọi $M[i]$ là giá trị nhỏ nhất trong block thứ $i$ và $D[i]$ là vị trí của giá trị nhỏ nhất này trong $A$. Cả $M$ và $D$ đều có $N/l$ phần tử. Tính Sparse Table cho $M$, tốn $O(N/l*log(N/l))=O(N)$ về bộ nhớ và thời gian.

Dùng sparse table cho mảng $M$, ta tính được giá trị nhỏ nhất của 1 vài block trong $O(1)$. Nhưng ta vẫn cần tính $RMQ$ giữa 2 vị trí bất kì trong cùng một block. Để làm được điều này, nhận thấy $B$ là một dãy nhị phân, mà mỗi block có $l$ phần tử. Vì số lượng dãy nhị phân độ dài $l$ là $2^l=\sqrt N$ là một số khá nhỏ nên chúng ta có thể tính được mảng $P[\sqrt(N)][l][l]$, với $P(b, i, j)$ là giá trị nhỏ nhất trong các bit từ $i$ đến $j$ của dãy nhị phân $b$. Dễ dàng khởi tạo $P$ bằng quy hoạch động trong cả thời gian và bộ nhớ $O(\sqrt N*l^2)$. Chú ý rằng, ta cũng cần biết giá trị $b$ trong $O(1)$ với mỗi block của mảng $A$. Do đó, ta cần khởi tạo mảng $T$ với $N/l$ phần tử, mỗi phần tử cho biết giá trị $b$ của block tương ứng.

Kết hợp mảng $T$, $P$ với Sparse table cho mảng $M$, ta có thể trả lời truy vấn $RMQ_A(i, j)$ trong $O(1)$. Ta có 2 trường hợp:

  1. $i$ và $j$ thuộc cùng block.
    • Ta dùng mảng $T$ để biết dãy nhị phân $b$ ở block chứa $i$ và $j$.
    • Tính $u$ và $v$ là vị trí của $i$ và $j$ trong block.
    • Kết quả chính là $P(b, u, v)$.
  2. $i$ và $j$ thuộc 2 block khác nhau: kết quả sẽ là giá trị nhỏ nhất của 3 giá trị:
    • Giá trị nhỏ nhất của các phần tử trong block chứa $i$ và nằm bên phải $i$:
    • Dùng mảng $T$ để biết được giá trị của dãy nhị phân của block chứa $i$ là $b$.
    • Tính chỉ số của $i$ trong block chứa $i$ là $u$.
    • Kết quả chính là $P(b, i, l)$. - Giá trị nhỏ nhất của các phần tử trong block chứa $j$ và nằm bên trái $j$: làm tương tự trường hợp trên - Giá trị nhỏ nhất của các phần tử thuộc các block nằm giữa block chứa $i$ và block chứa $j$. Dùng Sparse table cho $M$, ta dễ dàng tính được giá trị này trong $O(1)$.

Một số bài để luyện tập