Xác suất
Nguồn: Understanding Probabilities - Topcoder
Xác suất là một nhánh của Toán học có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong phân tích giá cả thị trường, chuẩn bị chiến lược trong thi đấu thể thao, dự báo thời tiết.. Bạn có thể đọc thêm về ứng dụng của xác suất trên Quora.
Đa số các bài toán về xác suất đều được lấy ví dụ từ thực tế. Ví dụ:
Kỳ thi sắp đến, có 20 chủ đề cần học và bạn chỉ có đủ thời gian để học 15 chủ đề. Nếu trong bài kiểm tra chỉ có 2 câu hỏi (mỗi câu hỏi về 1 chủ đề), thì xác suất bạn có thể trả lời đc cả 2 câu là bao nhiêu?
Không khó để nhận ra bài tập nào cần dùng kiến thức về xác suất nhưng giải được chúng là một câu chuyện hoàn toàn khác. Biết cách để tiếp cận những bài toán như vậy là một lợi thế lớn trong các cuộc thi lập trình, và bài viết dưới đây sẽ trang bị những kiến thức nền tảng cho bạn.
Cơ bản
Ta hình dung làm việc với xác suất như tiến hành một cuộc thí nghiệm. Tập hợp của tất cả những kết quả (outcome) có thể xảy ra của thí nghiệm được gọi là không gian mẫu (sample space), thường được kí hiệu bởi $S$. Mỗi kết quả có thể xảy ra được biểu diễn bởi một và chỉ một điểm trong không gian mẫu.
Chúng ta cùng xem xét ví dụ dưới đây:
- Tung xúc sắc một lần
- Không gian mẫu $S = {1,2,3,4,5,6} $
- Tung hai đồng xu
- Không gian mẫu $S = { (0, 0), (0, 1), (1, 0), (1, 1) }$ với 0 thể hiện đồng xu sấp và 1 thể hiện đồng xu ngửa.
Ta định nghĩa một biến cố (event) là một tập hợp các kết quả của một thí nghiệm. Do đó, một biến cố là một tập con của không gian mẫu $S$. Nếu ta đặt biến cố là $E$, thì $E \subseteq S$. Một biến cố có thể chỉ bao gồm một kết quả duy nhất trong không gian mẫu. Biến cố bao gồm nhiều hơn một kết quả được gọi là biến cố phức hợp (compound event), ví dụ như trong thí nghiệm tung 2 đồng xu ở trên.
Cái chúng ta quan tâm nhất là xác suất để một biến cố nhất định xảy ra, $P(E)$. Theo định nghĩa, $P(E)$ là một số thực trong khoảng từ $0$ đến $1$, trong đó $0$ thể hiện biến cố không có khả năng xảy ra và $1$ thể hiện biến cố chắc chắn xảy ra (hay là toàn bộ không gian mẫu).

- Impossible Event: biến cố chắc chắn ko thể xảy ra
- Certain: biến cố chắc chắn xảy ra
- Even chance: biến cố có xác suất 50-50.
Như đã đề cập, mỗi kết quả khả thi được biểu diễn bởi đúng một điểm trong không gian mẫu. Điều này đưa ta đến công thức:
$P(E) = \frac{\left | E \right |}{\left | S \right |}$
Nói cách khác, ta có thể tính xác suất để một biến cố xảy ra bằng cách chia số kết quả thuộc biến cố $E$ cho tổng số kết quả có thể xảy ra (theo không gian mẫu $S$). Để diễn tả mối quan hệ giữa các biến cố, bạn có thể dùng các quy ước từ lý thuyết về tập hợp. Xét trường hợp tung con xúc sắc một lần. Như trên, ta có $S = {1,2,3,4,5,6}$. Xem xét những biến cố dưới đây:
- Biến cố $A$: điểm > 3: ${4,5,6}$
- Biến cố $B$: điểm là số lẻ: ${1,3,5}$
- Biến cố $C$: điểm là 7: $\varnothing $
- $A \cup B$: điểm > 3 hoặc điểm là số lẻ: $={1, 3, 4, 5, 6}$
- $A \cap B$: điểm > 3 và là số lẻ: $ {5}$
- $A'$: biến cố A không xảy ra: ${1, 2, 3}$
Xác suất:
- $P(A \cup B) = 5/6$
- $P(A \cap B) = 1/6$
- $P(A’) = 1 – P(A) = 1 – 1/2 = 1/2 $
- $P(C) = 0$
Bước đầu tiên khi giải một bài toán về xác suất là xác định được không gian mẫu. Tiếp theo, bạn sẽ phải xác định số lượng phần tử của biến cố thỏa mãn. Đây là cách tiếp cận cơ bản, nhưng khi áp dụng, nó có thể thay đổi tùy vào từng bài tập.
Ví dụ
QuizShow (SRM 223, Div 1 – Easy).
Tóm tắt đề bài
Trong một cuộc thi, bạn đang đấu với 2 người nữa để tiến vào câu hỏi cuối cùng. Mỗi người đang sở hữu một số điểm nhất định giành được từ các câu hỏi trước. Tại câu hỏi này, mỗi người sẽ đưa ra số điểm cược trong khoảng từ 0 đến số điểm đang có, nếu trả lời đúng sẽ được số điểm cược này, trả lời sai sẽ bị trừ đúng bằng số điểm đã cược. Để chiến thắng, bạn phải là người sở hữu số điểm cao nhất sau khi hoàn thành câu hỏi cuối cùng.
Bạn biết điểm hiện tại của cả 3 người (số nguyên không quá $10^4$), và giá trị tiền cược của 2 người kia.
Hỏi bạn nên cược bao nhiêu để xác suất thắng là lớn nhất.
Phân tích
Mấu chốt để giải quyết bài toán là xét đến tất cả các khả năng có thể, số lượng này không nhiều. Sau một lúc đánh giá, ta sẽ xác định được không gian mẫu:
S = {
( người 1 đúng, người 2 sai, bạn sai),
( người 1 đúng, người 2 sai, bạn đúng),
( người 1 đúng, người 2 đúng, bạn sai),
( người 1 đúng, người 2 đúng, bạn đúng),
( người 1 sai, người 2 sai, bạn sai),
( người 1 sai, người 2 sai, bạn đúng),
( người 1 sai, người 2 đúng, bạn sai),
( người 1 sai, người 2 đúng, bạn đúng)
}Đề bài yêu cầu bạn tìm số tiền cược để tối đa số kết quả mà trong đó bạn thắng. Để đếm được số kết quả như vậy cho từng số tiến cược, ta cần xác định xem cả ba người chơi sẽ kết thúc với bao nhiêu điểm trong 8 trường hợp có thể xảy ra. Ý tưởng được thể hiện trong code dưới đây
int wager (vector scores, int wager1, int wager2)
{
int best, bet, odds, wage, I, J, K;
best = 0; bet = 0;
for (wage = 0; wage <= scores[0]; wage++)
{
odds = 0;
// 'odds' dem so ket qua tot
for (I = -1; I <= 1; I = I + 2)
for (J = -1; J <= 1; J = J + 2)
for (K = -1; K <= 1; K = K + 2)
if (scores[0] + I * wage > scores[1] + J * wager1 &&
scores[0] + I * wage > scores[2] + K * wager2) { odds++; }
// mot so tien cuoc tot hon duoc tim thay, cap nhat ket qua
if (odds > best) { bet = wage ; best = odds; }
}
return bet;
}Một bài thú vị khác là PipeCuts (SRM 233, Div 1 – Easy), bài này có thể giải bằng cách tương tự như trên.
Biến cố độc lập
Xét $n$ biến cố độc lập (independent events): $ E_1, E_2, …, E_n$ . Hai câu hỏi thường gặp là:
- Xác suất để tất cả biến cố xảy ra?: $P(all)$
- Xác suất để ít nhất một biến cố trong số chúng xảy ra? $P(any)$
Để trả lời câu hỏi thứ nhất, ta xét biến cố đầu tiên ($E_1$):
- Nếu $E_1$ không xảy ra, giả thuyết không còn đúng nữa.
- Vì vậy, phải chắc rằng $E1$ sẽ xảy ra với xác suất $P(E_1)$. Điều này có nghĩa là có xác suất $P(E_1)$ để ta kiểm tra sự xảy ra của biến cố tiếp theo (gọi là $E_2$).
- Biến cố $E_2$ xảy ra với xác suất là $P(E_2)$, và chúng ta có thể tiếp tục quá trình này tương tự như vậy.
Vì xác suất được định nghĩa là một số thực nằm trong khoảng từ 0 đến 1, ta tổng hợp được xác suất để tất cả các biến cố xảy ra bằng công thức dưới đây:
$P(all) = P(E_1) * P(E_2) * … * P(En) $
Cách tốt nhất để trả lời câu hỏi thứ hai là tìm xác suất để không có biến cố nào diễn ra và lấy phần bù.
$P(any) = 1 - P(E_1') * P(E_2') * … * P(E_n') $
Những công thức trên được ứng dụng rất nhiều, cần nắm chắc để đi đền phần tiếp theo.
BirthdayOdds
Một ví dụ điển hình để mô tả nội dung xác suất được bàn luận ở phần trên là Nghịch lí về ngày sinh (Birthday Paradox): Nếu có ít nhất 23 người trong một căn phòng, xác suất để 2 người bất kì trong số họ có cùng ngày sinh là lớn hơn 0.5. Thoạt nhìn, kết quả này có vẻ trái ngược với trực giác thông thường nhưng nó hoàn toàn có thể được chứng minh bằng toán học.
Bây giờ, một bài toán đặt ra là tìm số người nhỏ nhất để xác suất có ít nhất 2 người trong số họ cùng ngày sinh nhật là lớn hơn x %. Đôi khi trong các bài toán xác suất, cách tiếp cận dễ dàng hơn là thử giải bài toán ngược: "Tìm xác suất để $N$ người ngẫu nhiên có ngày sinh khác nhau?". Chiến thuật là bắt đầu với một cái phòng rỗng và lần lượt thêm từng người một vào và so sánh ngày sinh của người đó với tất cả những người đã có trong phòng.
int minPeople (int minOdds, int days) {
int nr;
double target, p;
target = 1 - (double) minOdds / 100;
nr = 1;
p = 1;
while (p > target) {
p = p * ( (double) 1 - (double) nr / days);
nr ++;
}
return nr;
}Các bài toán về xác suất có thể rất phức tạp và nhiều khi kết quả tạo cảm giác mâu thuẫn với những nhận đinh thông thường của chúng ta (Ví dụ như Nghịch lí về ngày sinh ở trên hoặc một ví dụ khác là Bài toán Monty Hall). Để có thể giải nhưng bài toán như vậy một cách thành thạo, ngoài việc nắm chắc các công thức toán học, các bạn cũng cần luyện tập cho mình một lối tư duy, trực giác toán học nhạy bén để tránh đưa ra những nhận định sai lầm về bài toán. Các bạn có thể làm bài kiểm tra để đánh giá trực giác toán học của mình.
Các kiến thức nâng cao
Biến ngẫu nhiên (Random variable)
Random Variable là một biến mà giá trị của nó là kết quả của một lần thí nghiệm. Ví dụ:
- $X1$ là giá trị của xúc sắc.
- $X2$ là 2 lần giá trị xúc sắc (có thể viết $2 * X1$)
- $X3$ là bình phương giá trị xúc sắc
- …
Giá trị kỳ vọng (Expected value):
Với $X$ là 1 random variable, $E(X)$ là giá trị trung bình của X, nếu ta thực hiện thí nghiệm vô số lần. Ta cũng có thể hình dung như giá trị trung bình có trọng số.
Ví dụ:
Có 2 lớp học:
- lớp A có 40 học sinh và điểm trung bình là 5
- lớp B có 30 học sinh và điểm trung bình là 6
Điểm trung bình của tất cả học sinh là:
(5 * 40 + 6 * 30) / (40 + 30) = 5 * (40 / 70) + 6 * (30 / 70)
Các trọng số $40 / 70$ và $30 / 70$ được nhân thêm do số lượng trường hợp điểm 5 và 6 khác nhau.
Công thức tổng quát:
E(X) = prob(X = 1) * 1 + prob(X = 2) * 2 + ...
Linearity of Expectation
Linearity of Expectation là 1 kĩ năng rất quan trọng nhất khi làm các bài về Expected value.
Ví dụ:
- Tung 2 xúc sắc
- Tính Expected value của tổng giá trị 2 xúc sắc.
Xét riêng từng xúc sắc:
- Đặt $E(X1)$ là expected value của giá trị xúc sắc 1
- Đặt $E(X2)$ là expected value của giá trị xúc sắc 2
$E(X1) = E(X2) = (1/6) * 1 + (1/6) * 2 + … + (1/6) * 6 = 3.5$.
Linearity of Expectation cho ta công thức sau:
$E(X1 + X2) = E(X1) + E(X2) = 7$.
Phát biểu chính xác:
Nếu $X1$, $X2$, …, $Xk$ là các random variable có cùng không gian mẫu:
$E(X1 * a1 + X2 * a2 + … + Xk * ak) = a1 * E(X1) + a2 * E(X2) + … + ak * E(Xk)$.
Chú ý rằng các biến không cần độc lập.
Tính xác suất từng bước một
Trong phần dưới đây, chúng ta sẽ tiếp tục thảo luận một vài bài tập trên Topcoder mà trong đó: Xác suất của một biến cố bị ảnh hưởng bởi biến cố khác.
Chúng ta có thể hình dung nó như một đồ thị mà trong đó:
- Mỗi nút là một biến cố
- Mỗi cạnh thể hiện sự phụ thuộc giữa các biến cố.
So sánh này hơi gượng ép, nhưng cách chúng ta tính toán xác suất cho các biến cố rất giống cách chúng ta duyệt qua các đỉnh của đồ thị: Ta bắt đầu ở gốc - là trạng thái ban đầu và có xác suất là 1. Sau đó, ta xem xét các cạnh kề để đến các khả năng khác nhau kèm theo các xác suất tương ứng.
Nested Randomness
Tóm tắt đề bài:
Hàm random(N) trả về một số nguyên ngẫu nhiên trong khoảng từ $0$ đến $N-1$, mỗi số có xác suất được trả lại như nhau và bằng $1/N$.
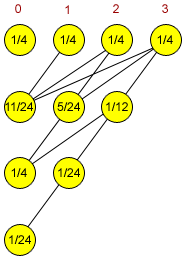
Giờ xét random(random(N)). Để dễ hình dung, ta xét $N=4$:
-
random(N)trả lại các số nguyên 0 đến 3 với xác suất bằng nhau là $1/4$. -
random(random(N)), ta có 4 trường hợp với xác suất bằng nhau (phụ thuộc vào kết quả của hàmrandombên trong):-
random(0): được gọi với xác suất $1/4$: báo lỗi -
random(1): được gọi với xác suất $1/4$: luôn trả về 0 -
random(2): được gọi với xác suất $1/4$: trả về 0 hoặc 1 với xác suất $1/2$. -
random(3): được gọi với xác suất $1/4$: trả về 0, 1, hoặc 2 với xác suất $1/3$.
-
- Nếu xét tiếp
random(random(random(N))):-
random(0): được gọi với xác suất $1/4 + 1/8 + 1/12 = 11/24$ -
random(1): được gọi với xác suất $1/8 + 1/12 = 5/24$ -
random(2): được gọi với xác suất $1/12$
-
- …
Ta hình dung bằng hình sau:
Code để giải bài này
double probability (int N, int nestings, int target) {
int I, J, K;
double A[1001], B[2001];
// A[I] la xac suat de so I xuat hien
for (I = 0; I < N ; I++)
A[I] = (double) 1 / N;
for (K = 2; K <= nestings; K++) {
for (I = 0; I < N; I++)
B[I] = 0;
// voi moi I giua 0 den N-1, ta goi ham random(I)
// theo yeu cau de bai
for (I = 0; I < N; I++)
for (J = 0; J < I; J++)
B[J] += (double) A[I] / I;
for (I = 0; I < N; I++)
A[I] = B[I];
}
return A[target];
}Bài tập tương tự:
GeneticCrossover
Khái niệm
Ở bài này có khái niệm về xác suất có điều kiện (conditional probability):
Xác suất có điều kiện là xác suất để một biến cố A nào đó xảy ra, biết rằng một biến cố B khác đã xảy ra.
Ký hiệu $P(A|B)$, và đọc là "xác suất của A, biết B". Nếu $A$ và $B$ là các biến cố, và $P(B) > 0$, thì xác suất có điều kiện của $A$ nếu biết $B$ là:
$P(A|B) = \frac{P(A \cap B)}{P(B)}$
Tương đương, ta có
$P(A \cap B) = P(A|B) P(B)$
Tóm tắt đề bài
Theo di truyền học ở động vật, mỗi cặp gen sẽ biểu thị một tính trạng. Mỗi gen có hai dạng cơ bản là trội hoặc lặn. Nếu trong cặp gen có gen trội thì tính trạng của gen trội này sẽ được thể hiện ra ngoài, ngược lại, trường hợp cả hai đều là gen lặn thì tính trạng của gen lặn này sẽ được thể hiện ra ngoài.
Ngoài ra, một số gen còn có tính phụ thuộc. Nếu một gen phụ thuộc vào một gen khác thì gen đó chỉ có thể thể hiện tính trội nếu gen nó phụ thuộc vào cũng thể hiện tính trội. Bên cạnh đó, có những gen không phụ thuộc vào bất cứ gen nào khác và tính trạng của nó sẽ được thể hiện như trong đoạn đầu. Đảm bảo không có trường hợp một gen phụ thuộc vào chính nó hay chuỗi phụ thuộc tạo thành một vòng (ví dụ I phụ thuộc J, J phụ thuộc K, K phụ thuộc I).
Cho $n$ cặp gen của cá thể bố mẹ và một số thông tin về chúng. Với mỗi cặp gen, cá thể bố/mẹ sẽ cho con của chúng một trong hai gen. Ví dụ như cá thể mẹ có hai chuỗi gen là ‘ABC’ và ‘abc’ thì với cặp gen đầu tiên, cá thể mẹ có thể cho cá thể con gen ‘a’ hoặc ‘A’, với cặp thứ hai là ‘b’ hoặc ‘B’ và cứ thế. Tương tự cá thể bố sẽ cho cá thể con một gen trong từng cặp như vậy. Sau cùng, cá thể con sẽ nhận được $n$ cặp gen từ bố và mẹ.
Chất lượng con giống của cá thể con được đánh giá dựa vào tính trạng thể hiện ở mỗi cặp gen. Nếu cặp gen thứ $i$ thể hiện tính trạng trội, chất lượng con giống sẽ được cộng thêm troi[i], còn nếu là tính trạng lặn thì sẽ cộng thêm lan[i].
Nhiệm vụ của bạn là tính giá trị kì vọng của chất lượng con giống.
Bạn sẽ được cung cấp 2 chuỗi gen thể hiện $n$ $(n \le 50)$ cặp gen của cá thể mẹ; 2 chuỗi gen thể hiện $n$ cặp gen của cá thể bố; 1 mảng $n$ số nguyên thể hiện quan hệ phụ thuộc giữa các gen, 2 mảng $n$ số nguyên troi[i] va lan[i] là giá trị công thêm cho chất lượng con giống gen thứ $i$ thể hiện tính trạng trội / lăn.
Từ những dữ liệu trên, bạn cần xuất ra giá trị kì vọng cần tìm.
(ND: Giá trị kì vọng được tính bằng cách lấy tổng của tất cả tích các giá trị có thể xảy ra với xác suất để xảy ra giá trị đó. Ví dụ:
- Giá trị chất lượng con giống: xác suất để đạt giá trị này
- 17 : 0.5625
- 13 : 0.1875
- 9 : 0.25
Vậy giá trị kì vọng của chất lượng con giống sẽ là $17 * 0.5625 + 13 * 0.1875 + 9 * 0.25 = 14.25$)
Phân tích
Dựa vào mô tả đề bài, có hai trường hợp có thể xảy ra: một gen không phụ thuộc vào gen khác, hoặc gen này có phụ thuộc.
Trường hợp thứ nhất, gọi $p$ là xác suất mà gen này là gen trội. Có 4 trường hợp:
- Ít nhất bố hoặc mẹ có hai gen trội ($p = 1$)
- Mỗi bố hoặc mẹ có đúng một gen trội ($p = 0.5$)
- Mỗi bố hoặc mẹ có một gen trội và người còn lại có duy nhất một gen lặn ($p = 0.25$)
- Cả hai bố mẹ có hai gen lặn ($p = 0$)
Trường hợp thứ hai, gen này có phụ thuộc vào một gen khác. Điều này làm bài toán trở nên phức tạp hơn do gen bị phụ thuộc có thể lại phụ thuộc vào một gen khác nữa và cứ thế… Do đó, để xác định được xác suất mà một gen phụ thộc là gen trội, ta cần xét xác suất để mỗi gen trong chuỗi phụ thuộc (bắt đầu từ gen đang xét) đều là gen trội. Xác suất để gen đang xét là gen trội sẽ bằng tích của tất cả các xác suất đó. Thuật toán thực hiện một cách đệ quy, và đây code hoàn chỉnh cho bài tập này:
int n, d[200];
double power[200];
// here we determine the characteristic for each gene (in power[I]
// we keep the probability of gene I to be expressed dominantly)
double detchr (string p1a, string p1b, string p2a, string p2b, int nr) {
double p, p1, p2;
p = p1 = p2 = 1.0;
if (p1a[nr] <= 'Z')
p1 = p1 - 0.5;
// is a dominant gene
if (p1b[nr] <= 'Z')
p1 = p1 - 0.5;
if (p2a[nr] <= 'Z')
p2 = p2 - 0.5;
if (p2b[nr] <= 'Z')
p2 = p2 - 0.5;
p = 1 - p1 * p2;
if (d[nr] != 1)
power[nr] = p * detchr (p1a, p1b, p2a, p2b, d[nr]);
// gene 'nr' is dependent on gene d[nr]
else power[nr] = p;
return power[nr];
}
double cross (string p1a, string p1b, string p2a, string p2b,
vector dom, vector rec, vector dependencies) {
int I;
double fitness = 0.0;
n = rec.size();
for (I = 0; I < n; i++)
d[i] = dependencies[i];
for (I = 0 ;I < n; I++)
power[i] = -1.0;
for (I = 0; I < n; i++)
if (power[I] == -1.0)
detchr (p1a, p1b, p2a, p2b, i);
// we check if the dominant character of gene I has
// not already been computed
for (I = 0; I <= n; I++)
fitness = fitness + (double) power[i] * dom[i]-(double) (1-power[i]) * rec[i];
// we compute the expected 'quality' of an animal based on the
// probabilities of each gene to be expressed dominantly
return fitness;
}Bài tương tự: ProbabilityTree
Thuật toán ngẫu nhiên
Ta gọi những thuật toán ngẫu nhiên là những thuật toán sử dụng hàm ngẫu nhiên để đưa ra quyết định trong quá trình chạy. Không giống như những thuật toán đã xác định trước, với mỗi dữ liệu vào xác định thì sẽ cho ra duy nhất một kết quả ra cũng như thời gian chạy, thuật toán ngẫu nhiên có thể biểu hiện khác nhau trong mỗi lần chạy. Về cơ bản, ta sẽ phân biệt hai loại của thuật toán ngẫu nhiên:
- Thuật toán Monte Carlo: có thể đưa ra kết quả sai - tuy nhiên xác suất của sai sót là chấp nhận được.
- Thuật toán Las Vegas: luôn cho kết quả đúng, và điểm khác biệt giữa các lần chạy với cùng một dữ liệu vào là thời gian chạy - ta sẽ nghiên cứu và sự phân phối theo xác suất của thời gian chạy.
Tham khảo tài liệu từ College of Engineering at UIUC để xem cách các thuật toán này hoạt động.
Mục tiêu chính của thuật toán ngẫu nhiêu là để tìm kiếm một hướng tiếp cận đơn giản hơn cho những bài toán phức tạp hoặc không có lời giải. Những thuật toán ngẫu nhiên không đảm bảo sẽ luôn tìm được kết quả tối ưu nhất, nhưng chúng có thể tìm được một kết quả đủ tốt trong một giới hạn về thời gian và bộ nhớ "chấp nhận được".
Một câu hỏi thú vị được đưa ra là liệu những thuật toán như vậy có ích trong các kì thi lập trình hay không. Khi bạn không nghĩ ra một cách nào để giải, hướng đi hợp lý là thử cài một cách random. Độ tốt của việc random phụ thuộc nhiều vào tính chất của bài toán, và khi có kinh nghiệm cũng như cảm nhận Toán học tốt, bạn có thể đoán được là random có thể chạy đúng được với bài toán hay không. Tham khảo QueenInterference
Trong các bài toán tối ưu hóa, nếu số nghiệm tối ưu khá nhiều so với số khả năng có thể xảy ra, một thuật toán random đơn giản như sau cũng có thể có hi vọng chạy đúng:
Max = 1000000; attempt = 0;
while (attempt < Max) {
answer = solve_random (...);
if (better (answer, optimum))
// Tìm được kết quả tốt hơn
{
optimum = answer;
cout << "Solution " << answer << " found on step " << attempt << "\n";
}
attempt ++;
}Bài tập luyện tập
ND: Mình không chép lại danh sách bài tập trong bài viết gốc ở Topcoder do sau này tác giả có thể chỉnh sửa hay bổ sung. Các bạn xem cuối bài viết gốc trên Topcoder để luyện tập thêm.