Nguồn: http://adilet.org/blog/25-09-14/

Cây Palindrome (hay còn được gọi là Eertree), được phát minh bởi Mikhail Rubinchik, là một loại cấu trúc dữ liệu được sử dụng để giải một số bài toán liên quan đến Palindrome.

Cấu trúc của cây Palindrome

Như mọi loại cây khác, cây Palindrome cũng có nút.

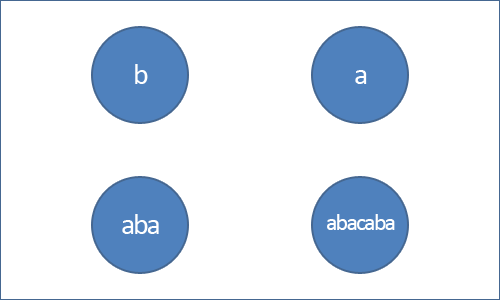
Ngoài nút ra cây còn có các cung để nối các nút. Cung nối giữa hai nút $u$ và $v$ được gán một chữ cái - ví dụ chữ X - nghĩa là ta có được palindrome chứa ở nút $v$ bằng cách thêm chữ X vào hai bên của palindrome chứa ở nút $u$.

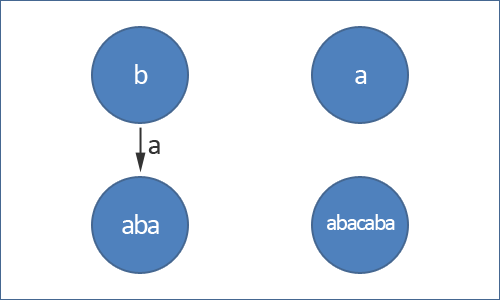
Trong ví dụ trên, ta có được xâu palindrome aba bằng cách thêm chữ a vào hai bên chữ b

Cuối cùng, ta có thêm các liên kết hậu tố. Nút $u$ có liên kết hậu tố đến nút $w$, nếu palindrome chứa ở nút $w$ là hậu tố không tầm thường lớn nhất của palindrome chứa ở nút $u$. (hậu tố là một xâu con chứa các chữ cái cuối cùng của xâu, hậu tố không tầm thường (proper suffix) là hậu tố của một xâu và ngắn hơn xâu đó). Từ bây giờ ta sẽ gọi palindrome lớn nhất mà là hậu tố không tầm thường của một xâu là palindrome hậu tố lớn nhất của một xâu.

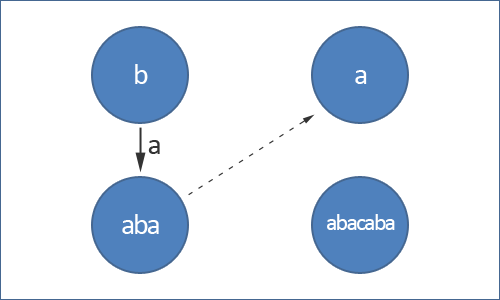
Trong ví dụ trên, vì a là palindrome hậu tố lớn nhất của aba nên có một liên kết hậu tố từ nút chứa xâu aba đến nút chứa xâu a.

Đặt tên cấu trúc dữ liệu này là cây Palindrome có vẻ không hợp lí lắm, vì nó có tận 2 gốc. Một sẽ chứa xâu palindrome giả độ dài -1. Gốc này giúp ta cài đặt cây dễ dàng hơn, vì khi ta thêm hai chữ cái bất kì vào hai bên xâu độ dài -1 thì ta sẽ được xâu độ dài 1 và nó luôn là palindrome. Gốc thứ hai chứa một xâu rỗng (xâu có độ dài 0), và xâu này cũng là palindrome. Ta cho thêm một liên kết hậu tố từ hai gốc nối đến gốc chứa palindrome độ dài -1.

Lưu ý rằng ta không chứa xâu palindrome vào nút khi cài đặt thực tế, nếu làm vậy ta sẽ tiêu tốn quá nhiều bộ nhớ. Nút thực tế sẽ chứa độ dài xâu palindrome, chữ cái được gán vào các cung, và các liên kết hậu tố.

Xây dựng cây Palindrome

Ở đây mình sẽ hướng dẫn tạo cây Palindrome chứa tất cả các palindrome con của một xâu s. Ta thấy: Một xâu độ dài $n$ sẽ không có quá $n$ xâu palindrome con, vì vậy cây Palindrome sẽ không có quá $n$ + 2 nút (do phải thêm 2 gốc nữa).

Ta sẽ xử lí từng chữ cái một trong xâu. Giả sử ta đã xử lí được tiền tố $p$ của xâu, và giờ ta phải xét đến chữ cái $x$ tiếp theo.

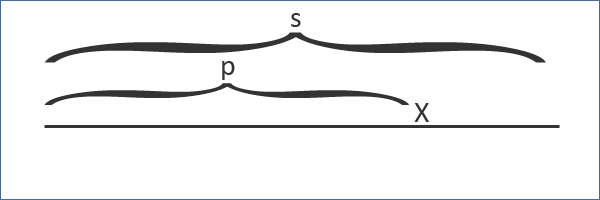
Ta lưu lại $t$ là palindrome hậu tố lớn nhất của tiền tố $p$.

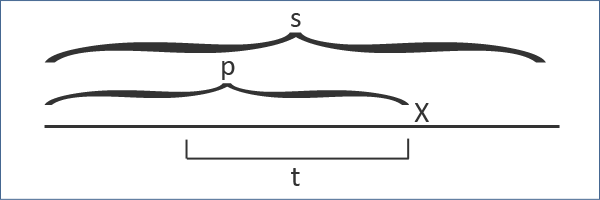
Vì $t$ đã được xử lí, nên nó được chứa trong một nút nào đó của cây Palindrome. Nút này sẽ có liên kết hậu tố đến một nút nào đó, nút nào đó lại có một liên kết hậu tố đến một nút khác và cứ tiếp tục như vậy.

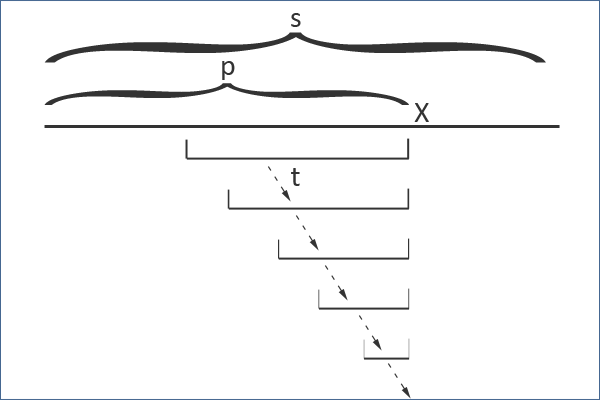
Bây giờ ta hãy tìm hậu tố palindrome của tiền tố mới $p+x$. Hậu tố đó sẽ có dạng $xAx$, với $A$ là một xâu nào đó, có thể rỗng hoặc có độ dài -1. Vì $xAx$ là palindrome, nên $A$ cũng là palindrome, và nó là một hậu tố của $p$, vì vậy ta có thể tìm $A$ từ $t$ bằng các liên kết hậu tố.

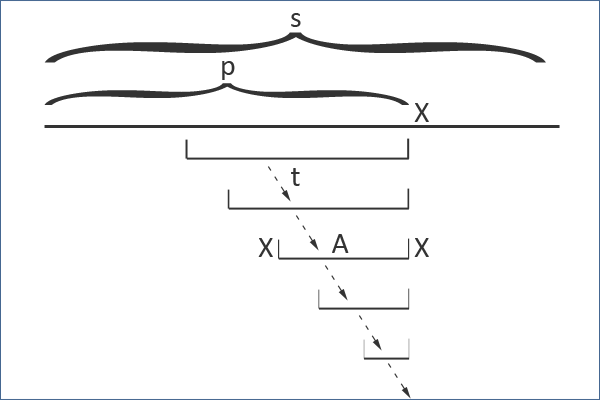
Xâu $xAx$ sẽ là xâu palindrome con duy nhất của xâu $p + x$ mà không xuất hiện ở xâu $p$. Thật vậy, ta thấy tất cả xâu palindrome con mới mà ta chưa thấy trong xâu $p$ phải kết thúc bằng chữ $x$, và do đó trở thành hâu tố của xâu $p + x$. Vì $xAx$ là hậu tố palindrome lớn nhất của $p + x$, tất cả các hậu tố palindrome nhỏ hơn nó có thể được tìm thấy trong một số tiền tố của $xAx$ (vì đối với bất kì hậu tố của palindrome có một tiền tố tương tự tương ứng), và vì thế ta đã thấy chúng trong $p$.

Vì vậy, để xử lí chữ cái $x$ thêm vào, ta phải đi theo các liên kết hậu tố của $t$ cho đến khi ta tìm thấy $A$ thích hợp (xâu $A$ thích hợp có thể có độ dài -1 nếu ta phải đi đến gốc). Sau đó ta kiểm tra xem có cung nào được gán chữ $x$ mà tương ứng với nút chứa xâu $A$, nếu không, thêm một cung được gán chữ $x$ nối từ nút chứa xâu $A$ đến nút mới chứa xâu $xAx$.

Bây giờ ta xét đến các liên kết hậu tố nối từ nút $xAx$. Nếu nút này đã có từ trước, nút này đã có các liên kết hậu tố và ta không phải làm gì cả. Nếu không, ta cần phải tìm palindrome hậu tố lớn nhất của $xAx$, có dạng $xBx$, mà $B$ là một xâu có thể rỗng. Bằng lập luận tương tự như trên, $B$ là palindrome hậu tố của $p$ và có thể đến được từ $t$ bằng các liên kết hậu tố.

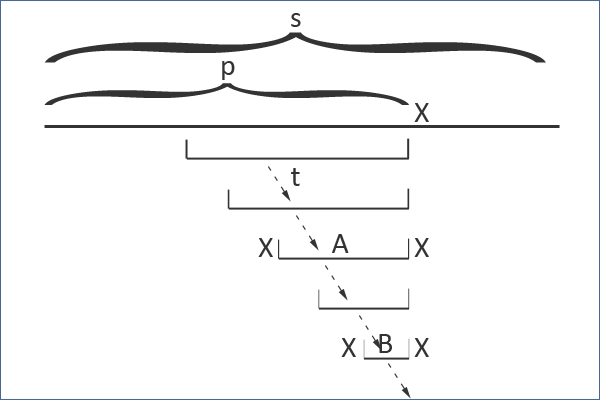
Vậy ta đã có được thuật toán xây dựng cây Palindrome. Xử lí từng chữ cái một, lưu trữ palindrome hậu tố lớn nhất $t$ của tiền tố đã xử lí (khởi tạo $t$ là xâu rỗng). Khi xử lí thêm chữ $x$, ta phải đi qua các liên kết hậu tố xuất phát từ $t$, cho đến khi ta tìm được palindrome $A$ thích hợp. Xâu $xAx$ sẽ trở thành sẽ trở thành hậu tố palindrome lớn nhất và trở thành nút duy nhất có thể chèn vào cây. Để tạo thêm các liên kết hậu tố ta phải đi theo các liên kết hậu tố cho đến khi tìm thấy xâu palindrome $B$, có thể thêm được hai chữ $x$ ở hai bên, rồi ta thêm liên kết hậu tố từ nút chứa xâu $xAx$ đến xâu $xBx$.

Để biết thêm thông tin chi tiết, bạn có thể tham khảo code. (bạn không cần chú ý đến biến $num$ vì nó được cho thêm vào để giải bài toán cụ thể). Bạn có thể thấy code không quá dài cũng như việc cài đặt rất đơn giản.

Độ phức tạp

Xét quá trình xây dựng cây Palindrome cho một xâu độ dài $n$. Ta thấy rằng khi ta xử lí từng chữ cái một, đầu của liên kết hậu tố palindrome lớn nhất của tiền tố được xử lí luôn di chuyển sang bên phải. Do đó, độ phức tạp của việc xây dựng cây Palindrome là $O(n)$.

Ứng dụng

Đếm số lượng palindrome xuất hiện thêm

Bài toán: Cho thêm chữ cái $x$ vào cuối xâu $S$, đếm số lượng palindrome xuất hiện thêm trong xâu $S$. Ví dụ khi ta cho thêm chữ cái a vào cuối xâu aba, ta có thêm một palindrome nữa là aa.

Lời giải khá là rõ ràng: Ta xây dựng cây Palindrome cho xâu $S$ ban đầu, và với mỗi chữ cái mới thêm vào, ta biết được số palindrome mới xuất hiện thêm bằng cách đếm số nút vừa được tạo ra trên cây Palindrome. Lưu ý: số palindrome xuất hiện thêm sau khi thêm một chữ cái vào một xâu bằng 1 hoặc bằng 0.

Đếm số lượng xâu con liên tiếp là palindrome

Code giải bài này bằng cây Palindrome đã có ở trên. Bài toán này còn có thể giải bằng thuật toán Manachar, tuy vậy ta nên giải bằng cây Palindrome vì cây Palindrome còn có thể ứng dụng cho nhiều bài toán khác.