FFT
Tác giả: ngmq
Trong bài này chúng ta sẽ tìm hiểu về thuật toán nhân nhanh hai đa thức sử dụng phép biến đổi Fourier nhanh (Fast Fourier Transform - FFT) và cách cài đặt của nó. Bài viết này sẽ chỉ nêu chứng minh sơ lược của một vài tính chất được sử dụng. Các chứng minh chi tiết có thể tìm thấy ở mục tài liệu tham khảo phía cuối của bài viết.
Vài nét lịch sử
Phép biến đổi Fourier (Fourier Transform) là một trong số những phát kiến toán học đặc sắc có lịch sử hào hùng, gắn liền với những phát kiến khoa học và chiến tranh quân sự ở thế kỷ 19 và 20. Joseph Fourier (1768-1830) là một nhà khoa học làm việc trong đội quân thám hiểm Ai Cập của Napoleon từ năm 1798. Sau khi cách mạng Pháp kết thúc năm 1799, Fourier trở về Pháp và tham gia xây dựng lại đất nước trong vai trò một giáo sư của đại học École Polytechnique. Trong quá trình làm việc với các công trình xây dựng cầu đường và đóng tàu, ông đặc biệt quan tâm tới bài toán mô tả quá trình truyền dẫn nhiệt trong kim loại, điều dẫn tới sự ra đời của phép biến đổi Fourier liên tục vào năm 1807 trong một báo cáo của ông tại viện hoàng gia Paris. Trong đó, ông mô tả mọi hàm số, kể cả các hàm số không liên tục đều có thể được biểu diễn dưới dạng tổng của một số vô hạn các hàm số lượng giác. Phát biểu này của Fourier gây chấn động và ấn tượng tới mức nhà toán học Pháp cùng thời là Lagrange cho rằng việc nghĩ ra phát kiến này là gần như không thể ("nothing short of impossible") [1]. Trong hơn một trăm năm sau đó phép biến đổi Fourier trở thành một đối tượng nghiên cứu phổ biến và liên tục được phát triển, hoàn thiện bởi vô số các tên tuổi lớn của toán lý thuyết [2].
Trong khi phiên bản nguyên thủy có lịch sử hoành tráng như vậy, phép biến đổi Fourier nhanh, dù được cho là ra đời trước, lại được quan tâm chậm hơn nhiều. Người ta cho rằng những ý tưởng đầu tiên về biến đổi Fourier nhanh được phát triển bởi nhà toán học Đức Carl Friedrich Gauss (1777 - 1855) vào năm 1805 khi ông cố gắng xác định quỹ đạo của các thiên thạch [3], nhưng khi đó ông không công bố kết quả của mình. Mối liên hệ giữa Gauss và phép biến đổi Fourier nhanh chỉ được phát hiện khi các công trình của ông được tập hợp và công bố vào năm 1866. Mặc dù vậy, vào thời đó không có ai quan tâm tới công trình này vì lý thuyết độ phức tạp tính toán chưa phát triển (mãi tới năm 1936 Alan Turing mới phát triển mô hình tính toán đầu tiên, và phải tới năm 1965 thì lịch sử ngành nghiên cứu về độ phức tạp tính toán mới bắt đầu với công trình của Hartmanis và Stearns [4]). Cũng trong năm 1965 hai nhà toán học trong ban cố vấn khoa học của tổng thống Mỹ Kennedy là James Cooley và John Tukey đã tự tìm ra phép biến đổi nhanh Fourier trong khi thiết kế hệ thống phát hiện các vụ thử hạt nhân của chính quyền Xô Viết [3]. Kể từ thời điểm đó phép biến đổi nhanh Fourier mới chính thức được quan tâm và nghiên cứu ứng dụng trong rất nhiều các lĩnh vực nghiên cứu khác nhau của vật lý, sinh học, điện tử, y tế, điều khiển học…
Nghiên cứu chỉ ra rằng mắt và tai người, động vật có "cài đặt" sẵn thuật toán biến đổi Fourier để giúp chúng ta nhìn và nghe, vì vậy nó được GS Ronald Coifman của đại học Yale gọi là Phương pháp phân tích dữ liệu của tự nhiên ("Nature's way of analyzing data") [1].
Phép nhân hai đa thức
Cho hai đa thức $p(x), q(x)$ có bậc $d, e$ như sau:
$p(x) = a_0 + a_1 x + a_2 x^2 + ... + a_d x^d$ $q(x) = b_0 + b_1 x + b_2 x^2 + ... + b_e x^e$
Ta cần tìm tích $c(x)$ của hai đa thức trên, có dạng: $c(x) = p(x)q(x) = c_0 + c_1 x + c_x x^2 + ... + c_{d+e} x^{d+e}$
trong đó
Cách làm theo định nghĩa là ta nhân mỗi hệ số của $p(x)$ với tất cả các hệ số của $q(x)$ rồi cộng các hệ số của cùng tổng số mũ. Vì hai đa thức có $d+1$ và $e+1$ hệ số nên cách làm này có độ phức tạp là $O((d+1)(e+1)) = O(de)$. Khi $d$ và $e$ tương đối lớn cỡ $10^3$ hoặc $10^4$ trở lên thì độ phức tạp này là quá lớn để chạy trên máy tính, đặc biệt là các máy tính nhúng đòi hỏi tốc độ tính toán nhanh. Phép biến đổi FFT giúp thực hiện phép nhân nói trên trong độ phức tạp $O(N*logN)$ trong đó $N$ là lũy thừa của $2$ nhỏ nhất lớn hơn $d$ và $e$.
Biểu diễn đa thức qua ma trận Vandermonde
Kể từ phần này trở về sau, ta quy ước $n$ là số hệ số của đa thức (bậc $n-1$) và $n$ là một lũy thừa của 2 ($n = 2, 4, 8, 16, 32, 64…$).
Xét đa thức $p(x) = a_0 + a_1 x + a_2 x^2 + … + a_{n-1} x^{n-1}$ với bậc $n-1$ và các hệ số phức $a_i \in \mathbb{C}$. Biểu thức tính $n$ giá trị của $p(x)$ tại $n$ điểm $z_0, z_1, … z_{n-1}$ có thể biểu diễn qua phép nhân ma trận như sau:
$=$
Ma trận vuông $V$ kích cỡ $n*n$ của $z_{0:{n-1}}$ ở trên được gọi là ma trận Vandermonde. Ta có các định lý sau:
Định lý 1: Định thức của ma trận Vandermonde là $det(V) = \prod_{0 \leq i < j \leq n-1}(z_j - z_i)$
Chứng minh (sơ lược): Với mỗi hàng $i = 0, 1, …n-2$ của định thức ta liên tục thay hàng $j = i+1, i+2, …n-1$ bằng hiệu của các hệ số của hàng $j$ trừ đi hàng $i$. Đây là phép biến đổi cơ bản (elementary operation) nên giá trị định thức cần tính không đổi. Lấy nhân tử chung $z_j - z_i$ ở tất cả các hàng ra ngoài và xét tiếp hàng $i+1$. Sau khi xét xong $i = n-2$ ta được một ma trận chéo có đường chéo chỉ gồm $z_{ii} = 1$, định thức của ma trận này hiển nhiên bằng 1. Vì vậy định thức cần tính là tích của tất cả các nhân tử chung bỏ ra ngoài ở các bước trước đó.
Phép chứng minh bằng quy nạp có thể xem thêm tại đây
Định lý 2: Đa thức $p(x)$ được xác định duy nhất bởi các giá trị của nó $p(z_0), p(z_1), … p(z_{n-1})$ khi $n$ giá trị $z_0, z_1, … z_{n-1}$ phân biệt. Ta gọi đây là phép biến đổi ngược.
Chứng minh:
Coi phương trình $(1)$ là một hệ phương trình $n$ ẩn với bộ nghiệm $a_0, a_1, …a_{n-1}$. Để đa thức $p(x)$ xác định và duy nhất thì định thức của ma trận $V$ ở trên phải khác $0$. Theo Định lý 1 ta có điều phải chứng minh.
Hệ quả: khi $V$ khả nghịch, hệ số $a_0, a_1, …a_{n-1}$ được xác định thông qua tích của ma trận nghịch đảo $V^{-1}$ của $V$ và $p(z_0), p(z_1), …p(z_{n-1})$.
Từ định lý 2, ta thấy rằng 1 đa thức bất kỳ có 2 cách biểu diễn:
- Dùng $n$ hệ số $a_i$
- Dùng $n$ cặp giá trị $z_i, p(z_i)$.
Đây chính là nền tảng của việc tính nhanh tích của 2 đa thức sử dụng FFT:
- Chọn 1 dãy $z_i$ gồm $N$ phần tử. $z_i$ có thể chọn tuỳ ý miễn sao giá trị của chúng là đôi một khác nhau để các đa thức $p(x)$, $q(x)$ và $c(x)$ là xác định và duy nhất.
- Chuyển 2 đa thức $p(x)$ và $q(x)$ sang cách biểu diễn 2. (dùng FFT)
- Tính tích của 2 đa thức trong cách biểu diễn 2 trong $O(N)$. Điều này cực kỳ đơn giản, vì khi ta đã cố định dãy $z_i$, ta có thể tính tất cả $c(z_i) = p(z_i) q(z_i)$ trong $O(N)$.
- Chuyển đa thức $c(x)$ về cách biểu diễn 1 (dùng FFT).
Nghiệm nguyên thủy
Như đã phân tích ở trên, ta cần chọn dãy $z_i$ sao cho việc biến đổi đa thức giữa 2 cách biểu diễn có thể thực hiện một cách hiệu quả. Nếu ta chọn $z_i$ là các nghiệm nguyên thủy thoả mãn:
với $n$ như đã quy ước và cũng là số nghiệm của phương trình $(2)$ mà ta cần. Công thức Euler xác định nghiệm thứ $k$ của phương trình $(2)$ là
trong đó $w_n$ là nghiệm mũ 1:
Dễ thấy là nghiệm nguyên thủy thứ $k$ có thể được tính trong $O(1)$ với $n$ đã biết.
Một số tính chất đặc biệt của ma trận Vandermonde nghiệm nguyên thủy
Tính chất 1: Ma trận nghịch đảo $V^{-1}$ được tính theo công thức: $V^{-1}[i,j] = {V[i,j]^{-1} \over n}$ với $i, j = 0, 1,…n-1$ là chỉ số hàng và cột của ma trận.
Chứng minh (sơ lược): gọi $B$ là ma trận kích cỡ $n * n$ tạo bởi
Ta sẽ chứng minh tích $P = B * V = V * B = n * I$, trong đó $I$ là ma trận đơn vị.
Xét phép nhân hàng $i$ của ma trận $V$ và cột $k$ của ma trận $B$, ta có: $P[i, k] = \sum_{j=0}^{n-1}w_n^{ij}w_n^{-jk} = \sum_{j=0}^{n-1}w_n^{j(i-k)}$
- Nếu $i = k:$ $P[i, k] = P[i, i] = \sum_{j=0}^{n-1}w_n^0 = n \qquad \forall i = 0, 1, …n-1$.
- Nếu $i \neq k:$ $P[i, k] = \sum_{j=0}^{n-1}{w_n^{i-k}}^j = {1 - {w_n^{i-k}}^n \over {1-w_n^{i-k}}} = 0$
Vậy $P = nI$ hay là $V * B/n = B/n * V = I$, vậy $B = V^{-1}$.
Hệ quả: Độ phức tạp tính toán cho $V^{-1}$ bằng với độ phức tạp tính $V$.
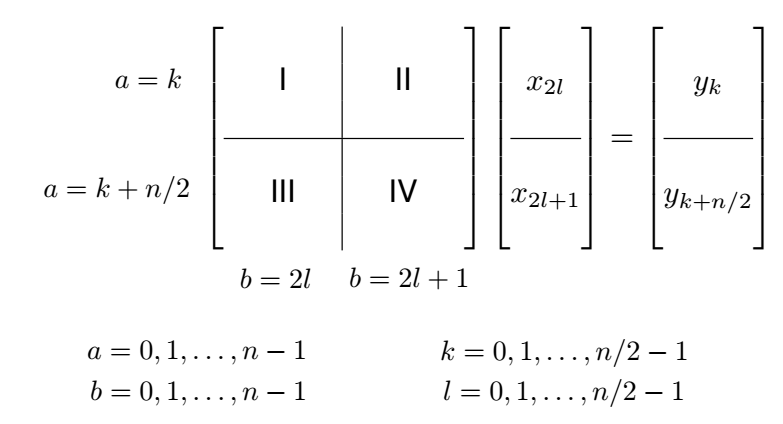
Tính chất 2: Chia ma trận $V$ thành $4$ phần bằng nhau kích cỡ $n/2 * n/2$ theo $2$ tiêu chí: độ lớn của hàng so với $n/2$ và tính chẵn lẻ của các cột.
- Phần $I$ gồm các phần tử có chỉ số hàng $0, 1,…n/2 - 1$ và chỉ số cột là chẵn $0, 2, 4, …n-2$.
- Phần $II$ gồm các phần tử có chỉ số hàng $0, 1,…n/2 - 1$ và chỉ số cột là lẻ $1, 3, 5, …n-1$.
- Phần $III$ gồm các phần tử có chỉ số hàng $n/2, n/2+1,…n-1$ và chỉ số cột là chẵn $0, 2, 4, …n-2$.
- Phần $IV$ gồm các phần tử có chỉ số hàng $n/2, n/2+1,…n-1$ và chỉ số cột là lẻ $1, 3, 5, …n-1$.
 (Image Courtesy of Aalto University)
(Image Courtesy of Aalto University)
Nói cách khác, ta tạo một ma trận mới $K$ bằng cách chuyển tất cả các cột có chỉ số chẵn của ma trận $V$ lên trước, các cột có chỉ số lẻ về sau, giữ nguyên thứ tự tương đối của các cột cùng chỉ số chẵn hoặc cùng chỉ số lẻ. Ở ma trận $K$ này cột $n-2$ của $V$ nằm ngay trước cột $1$ của $V$. Bốn phần $I, II, III, IV$ được tạo bởi cắt đều ma trận $K$ thành 4 phần bằng nhau.
Ký hiệu $K_I, K_{II}, K_{III}, K_{IV}$ là bốn ma trận con của $K$. Tất cả các phần tử trong phần $II, III, IV$ đều có thể tính được từ phần $I$ theo công thức sau:
$K_{II}[i, j] = w_n^i K_I[i,j] \qquad \forall i, j = 0, 1, ...n/2 - 1$ $K_{III}[i,j] = K_{I}[i,j] \qquad \forall i, j = 0, 1, ...n/2 - 1$ $K_{IV}[i, j] = -w_n^i K_I[i,j] \qquad \forall i, j = 0, 1, ...n/2 - 1$
Chứng minh: các bạn tự chứng minh hoặc xem slide số 23 trong tài liệu của trường DH Aalto ở phần tài liệu tham khảo.
Tính chất 3: ma trận nghịch đảo $V^{-1}$ cũng có thể chia thành $4$ phần bằng nhau với các phần $II, III, IV$ tính được qua phần $I$ giống như Tính chất 2.
Hệ quả: Phép biến đổi Fourier ngược (inverse Fourier transform) có cùng độ phức tạp với phép biển đổi Fourier.
Phép biến đổi Fourier nhanh
Trong phần trên ta đã thấy vai trò của ma trận Vandermonde $V$ là biến đổi một vector cột $a_0, a_1, …a_{n-1}$ thành một vector cột khác cùng kích cỡ $p(z_0), p(z_1), …p(z_{n-1})$. Phép biến đổi này được gọi là "Biến đổi Fourier rời rạc" (Discrete Fourier Transform). Lưu ý là mặc dù hai khái niệm "Biến đổi Fourier rời rạc" (DFT) và "Phép biến đổi Fourier nhanh" (FFT) là khác nhau nhưng vì khi cài đặt DFT người ta luôn sử dụng FFT nên hai khái niệm này được coi như đồng nhất.
Định lý 3: Tồn tại thuật toán biến đổi Fourier rời rạc có độ phức tạp là $O(nlog_2n)$.
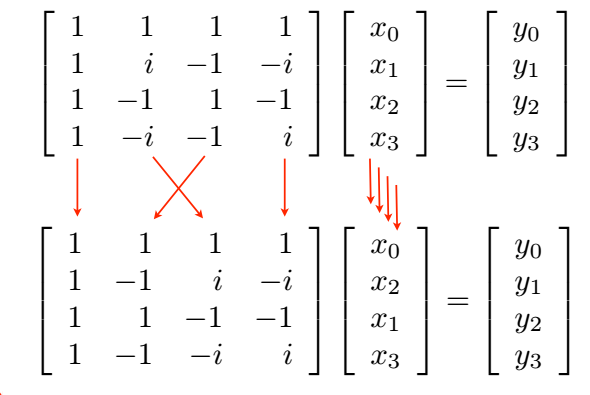
Chứng minh: Sử dụng lại ký hiệu trong hình vẽ ở phần trên, ta gọi $X$ là vector cần biến đổi Fourier và $Y$ là vector kết quả tương ứng. Thay vì sử dụng ma trận $V$ để nhân với $X$, ta sử dụng ma trận $K$ là kết quả của phép biến đổi như trong Định lý 2 để nhân với $X$. Lưu ý là vì $V$ đã đổi thứ tự cột nên $X$ cũng phải đổi thứ tự hàng: tất cả các hàng có chỉ số chẵn của $X$ được chuyển lên trên và các hàng chỉ số lẻ chuyển xuống dưới. Hình minh họa với $n = 4$ và $4$ nghiệm để thay vào ma trận Vandermonde là $1, i, -1, -i$:
 (Image Courtesy: Aalto University)
(Image Courtesy: Aalto University)
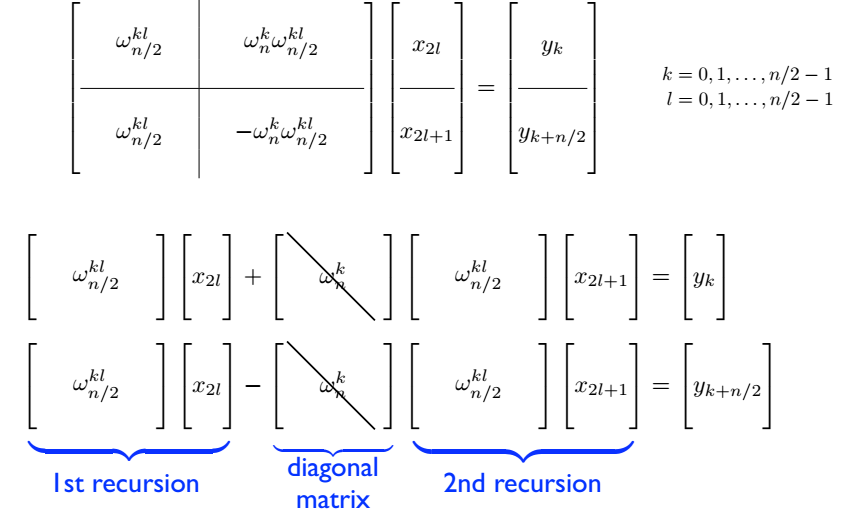
Tách vector kết quả $Y$ thành hai phần theo $n/2$, ta được:
 (Image Courtesy: Aalto University)
(Image Courtesy: Aalto University)
Ta quan sát là công thức tính nửa trên và nửa dưới của vector cột kết quả $Y$ sử dụng chung hai hạng tử và chỉ khác nhau về dấu của hạng tử thứ hai. Nói cách khác, chỉ cần tính được hai hạng tử tạo thành kết quả của vector kích cỡ $n/2$ là ta thu được kết quả của cả vector kích cỡ $n$ trong $O(n)$. Theo định lý tổng quát, độ phức tạp của cả quá trình là $O(nlog_2n)$
Công thức truy hồi: Từ tính chất đặc biệt của ma trận $K$, ta có công thức truy hồi để biến đổi một vector cột $X$ thành vector cột $Y$ như sau:
$FFT(x_{i=0, 1, 2,...n/2 - 1}) = FFT(x_{i=0, 2, 4, ...x_{n-2}}) + w_n^i FFT(x_{i=1, 3, 5...n-1})$ $FFT(x_{i=n/2, n/2+1, n/2+2,...n-1}) = FFT(x_{i=0, 2, 4, ...x_{n-2}}) - w_n^i FFT(x_{i=1, 3, 5...n-1})$
Thuật toán nhân hai đa thức
Đến đây ta đã có thể hoàn thiện chương trình nhân 2 đa thức $p(x), q(x)$ và lưu kết quả thành $h(x)$:
function NhânĐaThức( p(x), q(x), n )
// Lưu ý: n là số hệ số của đa thức kết quả
// Nếu p(x) có bậc d và q(x) có bậc e thì n = d + e + 1
fp[] = FFT(p(x), n) // biến đổi Fourier cho p(x) và lưu các giá trị vào mảng fp
fq[] = FFT(q(x), n) // biến đổi Fourier cho q(x) và lưu các giá trị vào mảng fq
for(i = 0; i < n; ++i)
fh[i] = fp[i] * fq[i]; // nhân tương ứng các giá trị của fp và fq, lưu vào mảng fh
h(x) = FFT_ngược(fh) // biến đổi Fourier ngược và lưu vào kết quả
end functionLưu ý về kỹ thuật cài đặt
Vì FFT đòi hỏi phải sử dụng số phức và (trong nhiều trường hợp) khử đệ quy nên có thể gây khó khăn cho các bạn chưa quen, phần này sẽ hướng dẫn sơ lược về cách cài đặt sử dụng C++.
Khai báo
Để sử dụng số phức trong C++ ta cần khai báo thư viện complex:
#include <complex>C++ cài đặt complex là một lớp (class) gồm 2 trường thực (real()) và ảo (imag()) nên khi sử dụng ta cần chỉ định kiểu dữ liệu cho hai trường này. Hai kiểu dữ liệu thông dụng là double hoặc long double:
typedef complex<double> base;
typedef vector<base> vb;Sau khi được định nghĩa bằng lệnh typedef thì để khai báo biến và vector kiểu phức, ta chỉ cần viết base x và vb v là được.
Một số phiên bản cài đặt tự định nghĩa lớp số ảo bằng một struct hoặc class. Nếu lớp tự viết này không có chức năng đặc biệt nào thì việc này là không cần thiết vì bản thân <complex> đã là một lớp rồi. Bạn có thể xem qua file thư viện trong thư mục cài đặt trình biên dịch, ví dụ với CodeBlocks thì đường dẫn có dạng CodeBlocks\MinGW\lib\gcc\mingw32\4.7.1\include\c++\complex (file ko có phần mở rộng).
Chuẩn hóa bậc đa thức
Trong các phần trên ta đã giả sử rằng $n$ là lũy thừa của $2$. Để đảm bảo tính đối xứng và thuận tiện khi cài đặt, nếu đề bài không cho trước $n$ bậc của đa thức là lũy thừa của $2$ thì ta cần chuẩn hóa thành số lũy thừa nhỏ nhất mà lớn hơn $n$. Chẳng hạn với $n = 10^5$ thì giá trị chuẩn hóa là $2^{17} = 131072$ vì $2^{16} = 65536 < 10^5$. Các hệ số của bậc cao hơn giá trị $n$ ban đầu gán bằng $0$.
Đệ quy và Khử đệ quy
Đệ quy:
Xét một đoạn mã C++ cài đặt hàm FFT sử dụng đệ quy như sau:
void fft_slow(int n, vb& a) // biến đổi fft của vector a, lưu kết quả vào chính nó
{
if(n == 1)
{
return;
}
int i, j, k;
// Bước 1. Khai báo kết quả fft chẵn và lẻ
vb a_even(n / 2), a_odd (n / 2);
// Bước 2. Tách hàng chẵn và hàng lẻ
for(i = j = 0; i < n; i += 2)
{
a_even[j] = a[i];
a_odd[j] = a[i+1];
++j;
}
// Bước 3. Biến đổi FFT với các hàng chẵn, lẻ
fft_slow(n / 2, a_even);
fft_slow(n / 2, a_odd);
// Bước 4: Ghép hoàn chỉnh kết quả
double ang = 2*PI/n;
base w (1), wn (cos(ang), sin(ang));
for(i = 0; i < n / 2; ++i)
{
a[i] = a_even[i] + w * a_odd[i];
a[i + n / 2] = a_even[i] - w * a_odd[i];
w *= wn;
}
}Có nhiều nguyên nhân làm cho FFT đệ quy chạy chậm, như trong Bước 1 thì khai báo hai vector kích cỡ $n/2$ lớn như vậy và lại khai báo liên tục ở các mức đệ quy. Bản thân chương trình đệ quy cũng chạy chậm vì chương trình phải lưu rất nhiều con trỏ stack và liên tục giải phóng bộ nhớ của biến cục bộ ở mỗi mức đệ quy. Nhìn chung đệ quy chỉ có ý nghĩa như trong thuật toán Quy Hoạch Động khi ta muốn tìm kết quả của một công thức truy hồi mà chỉ duyệt qua những trạng thái liên quan trực tiếp tới kết quả. Trong FFT ta luôn phải thăm hết các ma trận con nên cài đặt FFT bằng đệ quy không có lợi về tốc độ thực hiện.
Để cho đầy đủ thì ta cũng có hàm biến đổi FFT ngược như sau:
void inverse_fft_slow(int n, vb& a)
{
if(n == 1)
{
return;
}
int i, j, k;
vb a_even, a_odd;
for(i = 0; i < n; ++i)
{
if(i & 1) a_odd.push_back(a[i]);
else a_even.push_back(a[i]);
}
inverse_fft_slow(n / 2, a_even);
inverse_fft_slow(n / 2, a_odd);
double ang = -2*PI/n;
base w (1), wn (cos(ang), sin(ang));
for(i = 0; i < n/ 2; ++i)
{
a[i] = a_even[i] + w * a_odd[i];
a[i] /= 2;
a[i + n / 2] = a_even[i] - w * a_odd[i];
a[i + n / 2] /= 2;
w *= wn;
}
}Khử đệ quy:
Để khử đệ quy thì ta cần phân tích mối liên hệ giữa các lời gọi đệ quy và xem các phần tử được tính theo thứ tự nào. Hình vẽ sau đây minh họa trường hợp $n = 8$:
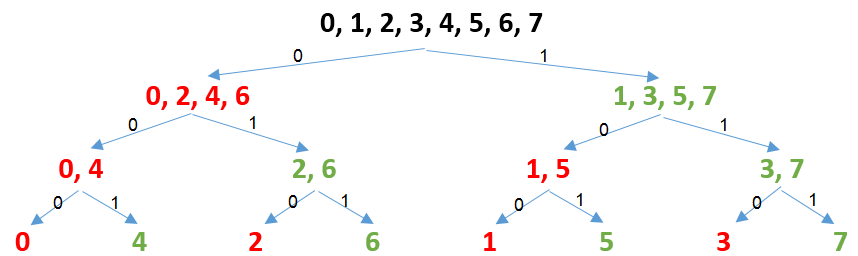
Màu đỏ là các nhóm chẵn và màu xanh là các nhóm lẻ. Các bạn hãy dựa vào tính chẵn lẻ và để ý các số nhị phân $0, 1$ trong hình vẽ để tự viết chương trình FFT khử đệ quy hoặc giải thích tính đúng đắn của đoạn mã sau (đây là hàm FFT đã được dùng để giải bài POST2)
#define PI acos(-1)
const int NBIT = 18;
const int N = 1<<18; // chuẩn hóa bậc của đa thức là 18
base W[N]; // mảng lưu các nghiệm nguyên thủy
// Hàm reverse bit: Đảo ngược nbit đầu tiên trong mã nhị phân của số mask
int revBit(int nbit, int mask)
{
int i, j;
for(i = 0, j = nbit - 1; i <= j; ++i, --j)
{
if( (mask >> i & 1) != (mask >> j & 1) )
{
mask ^= 1<<i;
mask ^= 1<<j;
}
}
return mask;
}
// Biến đổi FFT của mảng a
void fft(int n, vb& a)
{
if(n == 1)
return;
int i, j, k;
// Đi từ dưới lên trên của cây đệ quy: Hàng cuối cùng giá trị bằng với mảng được cho ban đầu nhưng hóa đổi vị trí
// theo số có biểu diễn nhị phân ngược với chỉ số
for(i = 0; i < n; ++i)
{
j = revBit(NBIT, i);
if(i < j) swap(a[i], a[j]);
}
vb anext(n); // hàng tiếp theo
// chiều cao cây bằng Log(n)
// biến "step" lưu số phần tử nằm trong một nhóm chẵn hoặc lẻ
for(int step = 1; step < n; step <<= 1)
{
double ang = PI / step ; //2*PI/(step * 2);
base w (1), wn (cos(ang), sin(ang));
// Lưu trước mảng nghiệm nguyên thủy
for(i = 0; i < step; ++i)
{
W[i] = w;
w *= wn;
}
// Cứ một nhóm chẵn và một nhóm lẻ cạnh nhau thì tạo thành kết quả cho hàng ở trên
// Duyệt qua tất cả các nhóm chẵn và nhóm lẻ cạnh nó
// even = chẵn, odd = lẻ
int start_even = 0;
int start_odd = start_even + step;
while(start_even < n)
{
for(i = 0; i < step; ++i)
{
anext[start_even + i] = a[start_even + i] + W[i] * a[start_odd + i];
anext[start_even + i + step] = a[start_even + i] - W[i] * a[start_odd + i];
}
start_even += 2*step;
start_odd = start_even + step;
}
for(i = 0; i < n; ++i)
a[i] = anext[i];
}
}Sau đây là cài đặt cho cả FFT xuôi và ngược. Biến invert = true cho FFT ngược.
void fft(int n, vb& a, bool invert)
{
if(n == 1)
return;
int i, j, k;
for(i = 0; i < n; ++i)
{
j = revBit(NBIT, i);
if(i < j) swap(a[i], a[j]);
}
vb anext(n);
for(int step = 1; step < n; step <<= 1)
{
double ang = PI / step;
if (invert) ang = -ang;
base w (1), wn (cos(ang), sin(ang));
for(i = 0; i < step; ++i)
{
W[i] = w;
w *= wn;
}
int start_even = 0;
int start_odd = start_even + step;
while(start_even < n)
{
for(i = 0; i < step; ++i)
{
anext[start_even + i] = a[start_even + i] + W[i] * a[start_odd + i];
anext[start_even + i + step] = a[start_even + i] - W[i] * a[start_odd + i];
}
start_even += 2*step;
start_odd = start_even + step;
}
for(i = 0; i < n; ++i)
a[i] = anext[i];
}
if (invert) {
for(i = 0; i < n; ++i)
a[i] /= n;
}
}Một số cách cài đặt khác sử dụng con trỏ cũng làm tăng tốc độ thực thi, có thể xem thêm trong trang của emaxx phần tài liệu tham khảo. Cũng trong trang của emaxx có thể tìm thấy cách cài đặt gộp hai hàm fft và inverse_fft lại làm một sử dụng một biến bool invert làm cho code ngắn gọn hơn.
Bài tập luyện tập
- VNOJ POST2
- FFT problems on Codeforces
- FFT problems by a2oj.com
- SumOfArrays - Topcoder SRM 603 và Hướng dẫn giải
Tài liệu tham khảo
- [1] Rohit Thummalapalli. Fourier Transform: Nature’s Way of Analyzing Data. Yale Scientific, 2010. Link
- [2] Alejandro Dominguez. Highlights in the History of the Fourier Transform. IEEE Pulse, 2016. Link
- [3] Stefan Woerner. Fast Fourier Transform. Numerical Analysis Seminar, Swiss Federal Institute of Technology Zurich, 2008. Link
- [4] Fortnow and Homer. A Short History of Computational Complexity. Bulletin of the European Association for Theoretical Computer Science 80, June 2003. Link
- Bài toán nhân đa thức, phép biến đổi Fourier nhanh trên csstudyfun.wordpress.com (có chứng minh các tính chất được đề cập trong bài
- Bài giảng của trường DH Aalto, Phần Lan
- Code cài đặt của e-maxx
- "Tutorial on FFT — The tough made simple." trên Codeforces