Thuật toán phân tách trọng tâm - Centroid decomposition
Tác giả:
- Cao Thanh Hậu - Trường đại học Khoa học Tự Nhiên - ĐHQG-HCM
Reviewer:
- Lê Minh Hoàng - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Ngô Nhật Quang - Trường THPT chuyên Khoa học Tự Nhiên - ĐHQGHN
Giới thiệu
Thuật toán phân tách trọng tâm có thể hiểu là thuật toán "chia để trị" trên cây. Thuật toán này hoạt động bằng cách liên tục chia nhỏ cây và xử lý trên mỗi cây được chia.
Trọng tâm của cây
Định nghĩa
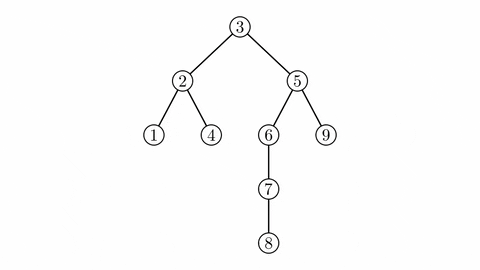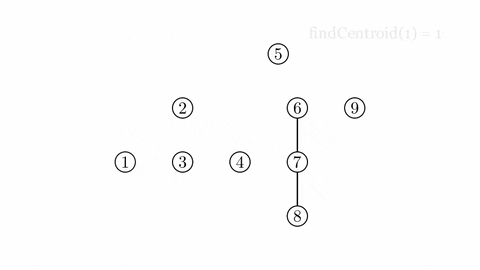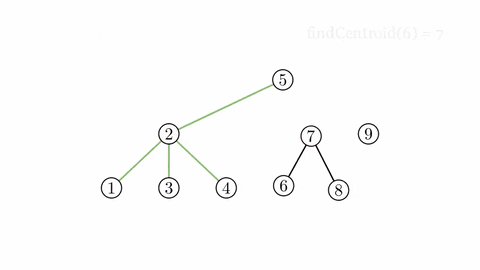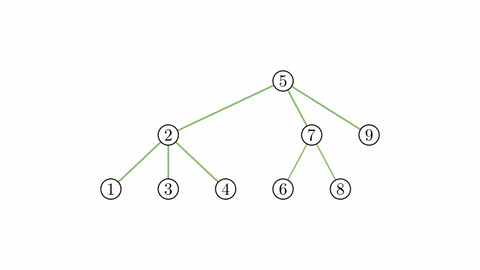
Trọng tâm của cây - centroid - là một đỉnh trên cây mà khi bỏ nó ra khỏi cây, mỗi thành phần liên thông còn lại có số đỉnh không quá một nửa số đỉnh của cây ban đầu.
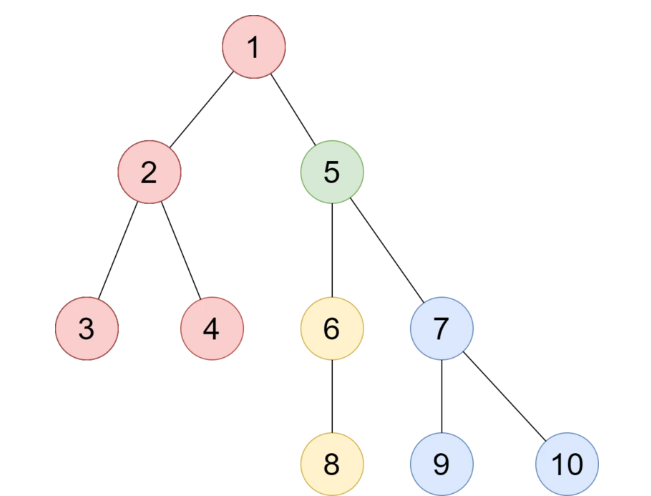
Cây trong hình trên có trọng tâm là đỉnh $5$.
Trọng tâm của cây có thể không độc nhất
Trong một số trường hợp, cây có thể có $2$ trọng tâm, và khi đó $2$ trọng tâm của cây sẽ kề nhau. Tuy nhiên, điều này không làm ảnh hưởng đến các thuật toán được nêu trong bài.
Tìm trọng tâm của cây
Từ định nghĩa, ta có ý tưởng cơ bản để tìm trọng tâm của cây như sau: giả sử trọng tâm của cây chắc chắn thuộc cây con gốc $u$, với mọi đỉnh $v$ là con trực tiếp của $u$, nếu cây con gốc $v$ có nhiều hơn $n/2$ đỉnh thì trọng tâm của cây chắc chắn thuộc cây con gốc $v$. Nếu không tìm được đỉnh $v$ nào thỏa mãn thì $u$ chính là trọng tâm của cây. Trong đó, $n$ là số đỉnh của cây.
Mở rộng ý tưởng, cần xây dựng hàm $findCentroid(u)$ với ý nghĩa: $findCentroid(u)$ được gọi chỉ khi trọng tâm cây chắc chắn thuộc cây con gốc $u$, và giá trị trả về của hàm luôn là trọng tâm của cây. Bên trong hàm này thực hiện tìm $v$ như ý tưởng cơ bản. Nếu tìm được $v$, trả về $findCentroid(v)$, nếu không tìm được thì trả về $u$.
Sau đây là code ví dụ, lưu ý trước khi tìm trọng tâm, ta cần gọi hàm $countChild(root, 0)$ để đếm số lượng đỉnh thuộc từng cây con. Để tìm centroid, gọi $findCentroid(root, 0)$, với $root$ là gốc của cây (có thể chọn bất cứ đỉnh nào).
int n; // n là số đỉnh của cây ban đầu
int child[N]; // child[u] là số đỉnh thuộc cây con gốc u
void countChild(int u, int parent) {
child[u] = 1; // cây con gốc u có ít nhất 1 đỉnh là đỉnh u
for (int v : adj[u]) { // với mọi v kề u
if (v != parent) { // nếu v là con của u
countChild(v, u);
child[u] += child[v];
}
}
}
int findCentroid(int u, int parent) {
for (int v : adj[u]) {
if (v != parent) {
if (child[v] > n/2) { // tìm được v thỏa mãn
return findCentroid(v, u);
}
}
}
return u; // không có giá trị v nào thỏa mãn, trả về u
}Code trên hoạt động với độ phức tạp là $O(n)$ (lưu ý, $n$ là số đỉnh của cây đang xét).
Từ định nghĩa hàm $findCentroid(u)$ cũng có thể chứng minh trọng tâm của cây luôn tồn tại. Khi $findCentroid()$ dừng lại tại đỉnh $u$ ($findCentroid(u)$ trả về $u$) ta biết rằng các cây con có gốc là con của $u$ đều đã thỏa mãn điều kiện có số đỉnh không vượt quá $n / 2$. Đồng thời khi $findCentroid(u)$ được gọi ta cũng biết số lượng đỉnh thuộc cây con gốc $u$ không nhỏ hơn $n / 2$, vậy số lượng đỉnh không thuộc cây con gốc $u$ cũng không vượt quá $n / 2$. Vậy khi xóa đỉnh $u$ đi thì mọi cây tạo thành đều có số đỉnh không vượt quá $n/2$.
Thuật toán phân tách trọng tâm - Centroid decomposition
Bài toán
Ta sẽ cùng giải quyết một bài toán điển hình như sau: Cho một cây có $n$ đỉnh, đếm số đường đi trên cây có độ dài $k$.
Phân tích
Nếu thêm điều kiện để bài toán trở thành "Đếm số đường đi trên cây độ dài $k$ đi qua một đỉnh cho trước" thì vấn đề đơn giản hơn khá nhiều.
Để giải quyết bài toán với điều kiện đi qua một đỉnh cho trước, ta chỉ cần chọn đỉnh đó là gốc, lúc này, với mỗi đỉnh $v$ là con trực tiếp của đỉnh gốc, mỗi đỉnh thuộc cây con gốc $v$ có khoảng cách đến gốc là $d$ có thể ghép với tất cả các đỉnh không thuộc cây con gốc $v$ và có khoảng cách đến gốc là $k - d$ để tạo thành một đường đi độ dài $k$ đi qua đỉnh gốc.
Có thể dfs để xây dựng các mảng đếm số lượng đỉnh có khoảng cách đến gốc là $0, 1, 2, 3,…$ trên cây và trong mỗi cây con gốc $v$, khi đó dễ dàng tính được số lượng đường đi thỏa mãn. Độ phức tạp của cách làm này là $O(n)$, với $n$ là số đỉnh của cây đang xét.
Trở lại bài toán ban đầu, làm sao để chuyển từ "số lượng đường đi chứa một đỉnh cố định" thành "số lượng đường đi trên cây"? Khi chọn một đỉnh làm gốc, thấy rằng mọi đường đi trên cây có thể chia thành 2 nhóm: đi qua đỉnh gốc và không đi qua đỉnh gốc. Từ đây ta có ý tưởng như sau: sau mỗi lần đếm số đường đi thỏa mãn đi qua một đỉnh cố định, ta xóa đỉnh đó đi, với mỗi cây mới tạo thành, ta lại thực hiện việc đếm như trên rồi lại xóa đỉnh đi, đến khi mọi đỉnh đều bị xóa.
Cách làm trên cho kết quả chính xác, vì mọi đường đi trên cây đều được xét qua và mỗi đường đi trên cây được xét qua đúng một lần (sau lần đầu tiên, một trong hai đầu mút của đường đi bị xóa hoặc sẽ thuộc về hai cây mới riêng biệt nhau, vì vậy sẽ không được xét lại lần hai).
Tuy nhiên, cách này có độ phức tạp khá lớn trong một số trường hợp. Ví dụ cây là đường thẳng, ta lại liên tục chọn một đầu mút của cây để làm đỉnh cố định, vậy sau mỗi lần xóa, số đỉnh trên cây chỉ giảm đi $1$, độ phức tạp tổng sẽ là $O(n + (n-1) + (n-2) + (n-3)+…) \approx O(n^2)$.
Thuật toán
Cũng theo ý tưởng trên, nhưng thuật toán phân tách trọng tâm cho cách chọn đỉnh tối ưu hơn, làm giảm độ phức tạp của thuật toán. Cụ thể, thuật toán hoạt động như sau:
- Chọn trọng tâm của cây làm gốc của cây.
- Đếm số lượng đường đi trên cây thỏa mãn yêu cầu và có chứa gốc của cây.
- Xóa đỉnh gốc. Nếu trước khi xóa cây có nhiều hơn $1$ đỉnh (khi đó tạo thành một hoặc một số cây riêng biệt khác) thì với mỗi cây mới được tạo, trở lại bước $1$.
Độ phức tạp của thuật toán bằng $\log(n)$ nhân cho độ phức tạp của bước $2$. Nếu bước $2$ được thực hiện trong $O(m)$, với $m$ là số đỉnh của cây đang xét lúc đó, thì độ phức tạp tổng sẽ là $O(n \times \log(n))$. Nếu bước $2$ được thực hiện trong $O(m\log(m))$, thì độ phức tạp tổng là $O(n \times \log(n)^2)$.
Giải thích
Giả sử ta xếp các cây được xét thành nhiều hàng, bắt đầu từ hàng $0$, mỗi hàng gồm một số cây theo quy luật: hàng $0$ chứa cây ban đầu, hàng thứ $i$ ($i$ từ $1$ trở đi) chứa các cây tạo được từ việc phân tách một cây nào đó ở hàng $i - 1$.
Xếp theo quy luật trên thì tổng kích thước (số đỉnh) của tất cả các cây trên một hàng không vượt quá $n$ (gọi $n$ là số đỉnh của cây ban đầu). Tất cả cây ở hàng thứ $i$ có kích thước không quá một nửa kích thước của cây to nhất ở hàng thứ $i - 1$, hay nói cách khác, mỗi cây ở hàng $i$ có số đỉnh không vượt quá $\frac{n}{2^i}$. Vậy chỉ có thể có nhiều nhất $log(n)$ hàng.
Vậy tổng số đỉnh của tất cả các cây tạo thành từ thuật toán trên không vượt quá $n \times \log(n)$, đây cũng chính là độ phức tạp của thuật toán.
Cài đặt
#include<bits/stdc++.h>
using namespace std;
const int N = 200005;
int n, k, child[N], del[N]; // del[u] để kiểm tra đỉnh u có bị xóa hay chưa
vector<int> adj[N];
void countChild(int u, int parent) {
child[u] = 1;
for (int v : adj[u]) if (v != parent && !del[v]) {
countChild(v, u);
child[u] += child[v];
}
}
int centroid(int u, int parent, int n) {
for (int v : adj[u])
if (v != parent && child[v] > n/2 && !del[v])
return centroid(v, u, n);
return u;
}
void updateAns(int root, int n) {
//hàm thực hiện bước 2
}
long long solve(int u) {
countChild(u, 0);
int n = child[u];
int root = centroid(u, 0, n); // bước 1
updateAns(root, n); // bước 2
del[root] = 1;
for (int v : adj[root]) if (!del[v])
ans += solve(v); // bước 3
return ans;
}
int main() {
cin >> n >> k;
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
cout << solve(1);
return 0;
}Mở rộng
Bước $2$ là bước quan trọng của thuật toán, có thể kiểm tra xem thuật toán có áp dụng được vào bài toán hay không bằng cách kiểm tra xem bước thứ $2$ có khả thi hay không. Bài toán ở bước $2$ thường đơn giản hơn nhiều so với bài toán ban đầu.
Bạn đọc có thể làm thử bài tập ví dụ tại đây
Cây trọng tâm
Cây trọng tâm $T'(V, E')$ của cây $T(V, E)$ có thể được xây dựng như sau: Thêm vào $E'$ các cạnh nối trọng tâm của $T$ với trọng tâm của mỗi cây mới tạo thành khi xóa trọng tâm của $T$ ra khỏi $T$. Với mỗi cây mới tạo được từ việc xóa trọng tâm, thực hiện lại việc thêm cạnh và xóa đỉnh như vừa nêu, tiếp tục đến khi tất cả các đỉnh đều bị xóa.
Sau khi xóa tất cả đỉnh trong cây $T$, ta đã xây dựng được cây $T'$ gọi là cây trọng tâm của cây $T$ ban đầu.
Cây trọng tâm có một số tính chất đặc biệt như:
- Cây có số lượng đỉnh bằng với cây ban đầu.
- Độ cao của cây không vượt quá $\log(n)$.
- $LCA(u, v)$ trên cây trọng tâm cũng thuộc đường đi từ $u$ đến $v$ trên cây ban đầu.
Từ các tính chất đó, ta có một ứng dụng vô cùng quan trọng của cây trọng tâm nói riêng hay thuật toán phân tách trọng tâm nói chung. Ứng dụng như sau:
Giả sử cần tính hàm $f(u, v)$ rất nhiều lần, với $f(u, v)$ là một hàm liên quan đến đường đi $u, v$, nghĩa là ta có thể tính $f(u, v)$ từ $f(u, k)$ và $f(k, v)$ với $k$ là một đỉnh thuộc đường đi $u, v$. Khi đó ta có thể tính trước tất cả các giá trị $f(u, p)$ với $p$ là tổ tiên của $u$ trên cây trọng tâm. Theo tính chất thứ $2$ thì chỉ có $n\log(n)$ cặp $(u, p)$, có thể áp dụng thuật phân tách trọng tâm để tìm tất cả các giá trị $f(u, p)$ đó. Vậy với hai đỉnh $u, v$ bất kì, ta có thể tính $f(u, v)$ từ $f(u, LCA_{ct}(u, v))$ và $f(v, LCA_{ct})$, trong đó $LCA_{ct}$ là tổ tiên chung gần nhất của $u$ và $v$ trên cây trọng tâm.
Nói đơn giản, vì độ cao của cây trọng tâm chỉ là $\log(n)$, vậy chỉ có tất cả $n\log(n)$ đường đi thẳng (đường đi từ một đỉnh đến một tổ tiên của đỉnh đó). Do đó, ta có thể tính trước tất cả giá trị của các đường đi có $2$ đầu mút là $2$ đầu của đường đi thẳng, từ đó tính giá trị của mọi đường đi trên cây bằng cách chia đường đi đó thành $2$ đường đi mà mỗi đường đi có $2$ đầu mút là $2$ đầu của một đường đi thẳng trên cây trọng tâm.
Đồng thời, việc tìm tổ tiên chung gần nhất trên cây trọng tâm có độ phức tạp vô cùng nhỏ. Độ phức tạp của thuật tìm $LCA$ là $\log(H)$ với $H$ là độ cao của cây. Với cây trọng tâm, $H = \log(n)$, vậy độ phức tạp cho mỗi lần tìm $LCA$ trên cây trọng tâm chỉ là $O(\log(\log(n)))$.
Áp dụng
Lampice - COCI 2019/2020
Tóm tắt đề bài
Cho một cây có $n$ đỉnh, mỗi đỉnh trên cây mang một kí tự. Tìm độ dài của đường đi dài nhất trên cây mà các kí tự trên đường đi đó tạo thành xâu đối xứng (gọi tắt là đường đi đối xứng).
Phân tích
Thoạt nhìn bài toán giống với các dạng bài dùng thuật phân tách trọng tâm (tìm đường đi thỏa điều kiện…), tuy nhiên bài toán ở bước $2$ là "tìm đường đi đối xứng dài nhất chứa đỉnh gốc" vẫn quá khó để giải quyết.
Vì vậy cần áp dụng thêm thuật toán chặt nhị phân để làm bài toán đơn giản hơn nữa.
Thuật toán chặt nhị phân áp dụng được nhờ tính chất: nếu tồn tại đường đi đối xứng độ dài $k$, thì cũng tồn tại đường đi đối xứng với bất kì độ dài nào nhỏ hơn $k$ và cùng tính chẵn lẻ với $k$ (và vì vậy mà ta cần chặt nhị phân hai lần, một để tìm đường đi đối xứng chẵn dài nhất và một để tìm đường đi đối xứng lẻ dài nhất).
Giải thích đơn giản, nếu tồn tại đường đi đối xứng độ dài $k$, ta có thể bỏ đi hai đầu mút của đường đi để còn lại đường đi độ dài $k - 2$, và vẫn đối xứng.
Khi đã áp dụng chặt nhị phân, bài toán còn lại "liệu có tồn tại đường đi đối xứng độ dài $k$ hay không?"
Bài toán này có thể giải quyết bằng thuật toán phân tách trọng tâm.
Ta cần giải quyết câu hỏi: "có tồn tại đường đi đối xứng độ dài $k$ và chứa đỉnh gốc của cây hay không?".
Câu hỏi có phần tương tự như vấn đề cần giải quyết ở bài tập trước, tuy nhiên có thêm điều kiện "đối xứng".
Gọi $s(u, v)$ là xâu tạo bởi đường đi từ $u$ đến $v$.
Ý tưởng như sau, với $2$ đỉnh $u, v$ mà đường đi từ $u$ đến $v$ có chứa đỉnh gốc và có độ dài là $k$, để kiểm tra xâu đối xứng, ta kiểm tra $s(u, v)$ có bằng $s(v, u)$ hay không, hay kiểm tra $s(u, root_u) + s(root, v) = s(v, root_v) + s(root, u)$ hay không? (gọi $root_u$ là con trực tiếp của $root$ mà là tổ tiên của $u$).
Áp dụng thuật toán $hash$ để kiểm tra, ta cần tìm trước các giá trị $hshdown[u]$, $hshup[u]$ với ý nghĩa lần lượt là hash của $s(root, u)$ và hash của $s(u, root_u)$. Từ các giá trị $hshdown, hshup$ của $u, v$ và các giá trị $k, h$, ta có thể áp dụng và biến đổi phương trình $s(u, root_u) + s(root, v) = s(v, root_v) + s(root, u)$ sao cho mỗi vế độc lập về $u$ hoặc $v$, từ đó giải quyết tương tự như bài tập trước.
Cài đặt
Dưới đây là một code đã ac bài Lampice, bạn đọc có thể tham khảo.
#include <bits/stdc++.h>
#define For(i, a, b) for (int i=a;i<=b;++i)
using namespace std;
const int N = 200005;
const long long base = 35711;
const long long mod = 1e9 + 7;
int n, Len, maxDep, child[N], valid[N];
char a[N];
vector<pair<int, long long>> b;
long long pw[N];
vector<int> adj[N];
unordered_map<long long, bool> f[N];
void countChild(int u, int p)
{
child[u] = 1;
for (int v : adj[u]) if (v != p && valid[v])
{
countChild(v, u);
child[u] += child[v];
}
}
bool dfs(int u, int p, int h, long long hshdown, long long hshup)
{
if (h > Len) return false;
if (p)
hshdown = (hshdown * base + a[u]) % mod;
hshup = (hshup + 1LL * a[u] * pw[h - 1]) % mod;
long long x = (hshup * pw[Len - h] - hshdown + mod) % mod;
if (!p) f[h][x] = true;
if (f[Len - h + 1].find(x) != f[Len - h + 1].end() )
return true;
for (int v : adj[u]) if (v != p && valid[v])
{
if (!p) b.clear();
if (dfs(v, u, h + 1, hshdown, hshup))
return true;
if (!p)
for (pair<int, long long> x : b) f[x.first][x.second] = true;
}
maxDep = max(maxDep, h);
b.push_back({h, x});
return false;
}
bool CD(int u, int n)
{
countChild(u, 0);
int flag = 1, half = n / 2;
while (flag)
{
flag = 0;
for (int v : adj[u])
if (valid[v] && child[v] < child[u] && child[v] > half)
{
u = v;
flag = 1;
break;
}
}
childCounting(u, 0);
if (dfs(u, 0, 1, 0, 0)) return true;
For(i, 1, maxDep) f[i].clear();
maxDep = 0;
valid[u] = false;
for (int v : adj[u]) if (valid[v])
if (CD(v, child[v])) return true;
return false;
}
bool check(int len)
{
Len = len;
For(i, 1, n) valid[i] = 1, f[i].clear();
return CD(1, n);
}
void solve()
{
cin >> n;
For(i, 1, n) cin >> a[i];
For(i, 1, n - 1)
{
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
pw[0] = 1;
For(i, 1, n) pw[i] = pw[i - 1] * base % mod;
int l = 0, r = (n - 1) / 2;
while (l < r)
{
int g = (l + r + 1) / 2;
if (check(g * 2 + 1)) l = g; else r = g - 1;
}
int ans = r * 2 + 1;
l = 0, r = n / 2;
while (l < r)
{
int g = (l + r + 1) / 2;
if (check(g * 2)) l = g; else r = g - 1;
}
cout << max(ans, r * 2);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
solve();
return 0;
}QTREE5
Tóm tắt đề bài
Cho một cây có $n$ đỉnh, ban đầu mỗi đỉnh đều có màu đen. Thực hiện $q$ truy vấn, mỗi truy vấn thuộc một trong hai loại sau đây:
- $0$ $u$: đổi màu đỉnh $u$ (nếu $u$ đang có màu đen thì đổi thành trắng, nếu $u$ có màu trắng thì đổi thành đen).
- $1$ $u$: tìm khoảng cách từ đỉnh $u$ đến đỉnh màu trắng gần nhất. Nếu không có đỉnh nào màu trắng, in $-1$.
Phân tích
Xây dựng cây trọng tâm của cây được cho, gọi $LCA_{ct}(u, v)$ là tổ tiên chung gần nhất của $u$ và $v$ trên cây trọng tâm. Gọi $dist(u, v)$ là khoảng cách giữa đỉnh $u$ và đỉnh $v$ trên cây ban đầu.
Khoảng cách giữa $2$ điểm $u$, $v$ bất kì có thể phân tích như sau: $dist(u, v) = dist(u, LCA_{ct}(u, v)) + dist(LCA_{ct}(u, v), v).$ Bằng thuật toán phân tách trọng tâm, ta có thể tính trước mọi giá trị $dist(u, p)$ mà $p$ là tổ tiên của $u$ trên cây trọng tâm.
Với mỗi truy vấn, đỉnh $u$ là cố định, ta cần xét qua các đỉnh $v$ màu trắng để tìm $dist(u, v)$ nhỏ nhất. Thấy rằng, có thể có nhiều nhất đến $n$ đỉnh $v$ màu trắng, tuy nhiên chỉ có nhiều nhất $log(n)$ giá trị $LCA_{ct}(u, v)$ khác nhau (tính chất về chiều cao của cây trọng tâm), vì vậy có thể xem xét việc "xử lý chung" cho các đỉnh $v$ mà $LCA_{ct}(u, v)$ cố định.
Với mỗi đỉnh, ta cần $1$ multiset để lưu tất cả các khoảng cách từ đỉnh đó đến một đỉnh con màu trắng của nó trên cây trọng tâm, tổng kích thước của các multiset không quá $nlog(n)$. Với mỗi truy vấn đổi màu đỉnh $u$, ta có thể duyệt qua tất cả các đỉnh tổ tiên của $u$ trên cây trọng tâm để cập nhật các multiset cần thiết.
Về truy vấn tìm khoảng cách, ta cũng lại duyệt qua các đỉnh tổ tiên của $u$ trên cây trọng tâm. Tại đỉnh $p$ là tổ tiên của $u$, gọi $s_p$ là khoảng cách nhỏ nhất từ đỉnh $p$ đến một đỉnh màu trắng, ta có $dist(u, p) + s_p$ là độ dài nhỏ nhất của một đường đi từ đỉnh $u$ đến một đỉnh màu trắng và có đi qua $p$, đáp án cho truy vấn là giá trị $dist(u, p) + s_p$ nhỏ nhất khi xét tất cả các đỉnh $p$. Như vậy, bằng cách xét qua hết tất cả các đỉnh $p$ là tổ tiên của $u$ trên cây trọng tâm, ta đã bao quát tất cả các đường đi từ đỉnh $u$ đến một đỉnh trắng nào đó.
Độ phức tạp của thuật toán là $nlog^2(n)$
Lưu ý, giá trị $dist(u, p) + s_p$ đề cập ở trên có thể là giá trị của một đường đi "không chuẩn" - đường đi đi qua một cạnh nhiều lần. Tuy nhiên đường đi này chắc chắn có độ dài lớn hơn đường đi tối ưu, vì vậy ta chỉ cần quan tâm rằng đường đi tối ưu có được xét qua hay không, nếu có, kết quả tìm được là chính xác.
Cài đặt
#include <bits/stdc++.h>
using namespace std;
const int N = 2 * 1e5 + 5;
const int oo = 1e9 + 7;
int n, del[N], par[N], child[N];
vector<int> adj[N];
multiset<int> s[N];
map<int, int> d[N];
int countChild(int u, int p) {
child[u] = 1;
for (int v : adj[u]) {
if (v == p || del[v]) continue;
child[u] += countChild(v, u);
}
return child[u];
}
int centroid(int u, int p, int m) {
for (int v : adj[u]) {
if (v == p || del[v]) continue;
if (child[v] > m / 2)
return centroid(v, u, m);
}
return u;
}
void calcDist(int u, int p, int root) {
for (int v : adj[u]) {
if (v == p || del[v]) continue;
d[v][root] = d[u][root] + 1;
calcDist(v, u, root);
}
}
int cd(int u = 1) {
int m = countChild(u, 0);
u = centroid(u, 0, m);
calcDist(u, 0, u);
del[u] = 1;
for (int v : adj[u]) {
if (del[v]) continue;
int x = cd(v);
par[x] = u;
}
return u;
}
void solve()
{
int n; cin >> n;
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
int root = cd();
int q; cin >> q;
vector<int> col(n + 5, 1);
while (q--) {
int t, u; cin >> t >> u;
if (t == 0) {
int p = u;
col[u] ^= 1;
if (col[u]) {
while (p) {
s[p].erase(s[p].lower_bound(d[u][p]));
p = par[p];
}
}
else {
while (p) {
s[p].insert(d[u][p]);
p = par[p];
}
}
}
else {
int ans = oo, p = u;
while (p) {
if (s[p].size()) {
ans = min(ans, d[u][p] + *s[p].begin());
}
p = par[p];
}
if (ans >= oo) cout << "-1\n";
else cout << ans << "\n";
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
solve();
return 0;
}
Luyện tập
Bạn đọc cũng có thể tìm thêm bài tập về Centroid tại mục tag trên trang oj.vnoi.info/.