Heavy-Light Decomposition (HLD)
Tác giả:
- Phạm Hoàng Hiệp – University of Georgia
Reviewer:
- Nguyễn Minh Hiển - Trường Đại học Công Nghệ, ĐHQGHN
- Nguyễn Minh Nhật - Trường THPT chuyên Khoa học Tự nhiên, ĐHQGHN
- Đặng Đoàn Đức Trung - UT Austin
Mở đầu
Giới thiệu về HLD
Heavy-Light Decomposition (HLD), dịch ra tiếng Việt là phân chia nặng nhẹ là một kỹ thuật thường được dùng trong những bài toán xử lý trên cây.
Trong bài viết này, để ngắn gọn và dễ nhớ, chúng ta sẽ gọi tên kỹ thuật là HLD.
Tuy nghe tên có vẻ kinh khủng nhưng trên thực tế, đây là một kỹ thuật có ý tưởng khá tự nhiên và có tính ứng dụng cao, có thể được sử dụng trong nhiều bài tập.
Kiến thức cần biết
- Các thuật toán duyệt đồ thị cơ bản (DFS, BFS, …)
- Cây
- Lowest Common Ancestor (LCA) - Tổ tiên chung gần nhất
- Segment Tree
- Euler tour on tree (nên biết nhưng không bắt buộc)
Bài toán
Để trả lời câu hỏi HLD sẽ giúp chúng ta làm gì, chúng ta sẽ cùng giải một bài toán.
Trước hết, chúng ta sẽ đến với phiên bản dễ hơn của bài toán như sau.
Cho một mảng số nguyên dương gồm tối đa $10^5$ phần tử. Chúng ta cần xử lý tối đa $10^5$ truy vấn thuộc một trong hai loại sau:
- Cập nhật giá trị của phần tử thứ $i$ thành $x$
- Tính tổng XOR của tất cả các phần tử trong đoạn từ $l$ đến $r$
Bài toán trên là một bài toán quen thuộc và có thể được xử lý đơn giản bằng cách sử dụng Segment Tree. Nhưng, giả sử thay vì mảng một chiều, chúng ta cần xử lý bài toán trên cây thì phải làm như thế nào?
Phát biểu bài toán
Bạn đọc có thể đọc đề bài cụ thể và nộp code tại đây
Cho một cây (một đồ thị có $n$ đỉnh và $n-1$ cạnh và giữa hai đỉnh bất kỳ có đúng một đường đi giữa chúng). Mỗi đỉnh được gán một giá trị. Chúng ta cần xử lý hai loại truy vấn
- Cập nhật giá trị của đỉnh $i$ thành $x$
- Tính tổng XOR của tất cả các giá trị trên đường đi từ đỉnh $u$ đến đỉnh $v$
Đường đi từ $u$ đến $v$ trên đồ thị được định nghĩa là một chuỗi các đỉnh $u, w_1, w_2, …, w_k, v$ trong đó tồn tại một cạnh nối giữa $u$ và $w_1$, $w_1$ và $w_2$, …, $w_{k-1}$ đến $w_k$, $w_k$ đến $v$. Với mỗi cặp đỉnh $u$, $v$ bất kỳ trên cây tồn tại một và chỉ một đường đi từ $u$ đến $v$.
HLD
Ý tưởng chính
Vậy chính xác thì HLD sẽ làm gì để giúp chúng ta giải được phiên bản "trên cây" của bài toán trên? Liệu chúng ta có thể biến cây cho trước thành một mảng để giải bài toán trên đó? Câu trả lời là không. Tuy nhiên chúng ta có thể chia cây thành một số phần, và giải bài toán trên từng phần đó. Cụ thể như sau, giả sử có cây sau đây
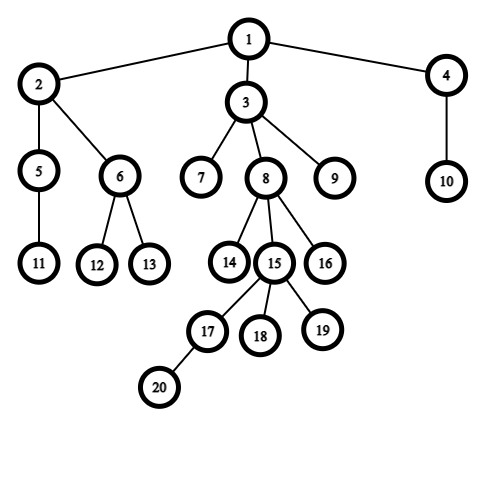
Không mất tính tổng quát, có thể coi đỉnh $1$ là gốc của cây. Với mỗi đỉnh không phải lá trên cây, chúng ta sẽ đánh dấu những cạnh nối đỉnh đó với con có kích thước cây con lớn nhất của của nó.
Ví dụ, xét đỉnh $15$ có ba đỉnh con lần lượt là đỉnh $17$, $18$ và $19$. Cây con ở hai đỉnh $18$ và $19$ có kích thước là $1$, còn cây con ở đỉnh $17$ có kích thước là $2$.
Vì vậy, chúng ta sẽ đánh dấu cạnh nối giữa đỉnh $15$ và đỉnh $17$ (tô màu đỏ). Làm tương tự với các đỉnh còn lại, chúng ta được cây như hình vẽ dưới đây.
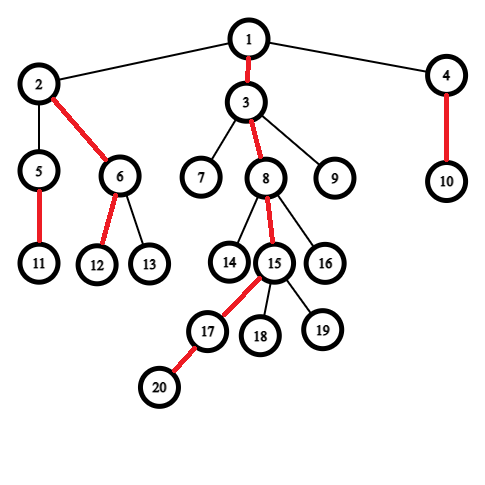
Chúng ta sẽ gọi những cạnh màu đỏ là những "cạnh nặng" (heavy edges) vì chúng nối một đỉnh với đỉnh con "nặng nhất". Những cạnh còn lại sẽ được gọi là những "cạnh nhẹ" (light edges)
Có thể thấy rằng, những cạnh được đánh dấu sẽ tạo thành các "chuỗi" đi từ trên xuống dưới. Ví dụ như chuỗi $1-3-8-15-17-20$ hay chuỗi $5-11$. Các đỉnh là lá cũng có thể coi là một chuỗi riêng.
Với cách quy ước trên, ta có thể thấy rằng hai chuỗi "liền nhau" được nối với nhau bởi một cạnh nhẹ. Hai chuỗi "liền nhau" là hai chuỗi mà tồn tại đỉnh $u$ nằm ở một chuỗi và $v$ nằm ở chuỗi còn lại sao cho $u$ và $v$ có cạnh nối trực tiếp với nhau. Do $u$ và $v$ khác chuỗi nên cạnh nối giữa $u$ và $v$ là cạnh nhẹ. Hai chuỗi không thể nối ở nhiều hơn một cặp điểm.
Khi đó, chúng ta có thể chứng minh được rằng đường đi giữa hai đỉnh bất kỳ trên cây đi qua không quá $O(\log(n))$ chuỗi. Bạn đọc có thể tự chứng minh nhận xét trên trước khi đọc chứng minh bên dưới.
Chứng minh
Xét một đỉnh $v$ được nối với đỉnh cha của nó là $p$ bởi một cạnh nhẹ. Giả sử kích thước cây con của $v$ là $x$ và kích thước cây con của $p$ là $y$. Do cạnh nặng đi từ $p$ không được nối xuống $v$ nên chắc chắn tồn tại một con khác của $p$ là $u$ có kích thước cây con $\geq x$. Vì vậy, $y \geq 2 * x$ Do với mỗi lần nhảy qua cạnh nhẹ, kích thước của cây con ở đỉnh sau khi nhảy sẽ tăng ít nhất là gấp đôi nên ta có thể kết luận rằng để đi lên một tổ tiên bất kỳ ở phía trên thì có thể nhảy qua không quá $\log_2(n)$ cạnh nhẹ. Do mỗi lần đi qua cạnh nhẹ chính là một lần nhảy sang chuỗi mới nên từ một đỉnh $v$ lên tổ tiên bất kỳ của nó sẽ chỉ đi qua $O(\log(n))$ chuỗi. Khi đó, từ hai đỉnh $u$, $v$ bất kỳ, chúng ta có thể tìm LCA của $u$, $v$ và đi từ $u$, $v$ đến LCA. Số chuỗi đi qua sẽ không quá $O(\log(n))$
Ngoài ra, nếu ta duyệt cây bằng DFS ưu tiên các đỉnh liền trong chuỗi trước, ta có thể nhận thấy là các đỉnh trên cùng một chuỗi sẽ nằm kế tiếp nhau trên thứ tự DFS, và vì thế việc truy vấn một đoạn con bất kì trên một chuỗi nào đó có thể được thực hiện trên Segment tree với độ phức tạp là $O(\log(n))$.
Như vậy, chúng ta đi qua không quá $O(\log(n))$ chuỗi, với mỗi chuỗi chúng ta có thể thực hiện trả lời truy vấn hoặc update trong $O(\log(n))$ trên Segment tree nên độ phức tạp cho việc trả lời các truy vấn và cập nhật trên một đường đi giữa hai đỉnh bất kỳ trên cây là $O(\log^2(n))$
Chi tiết cài đặt
Thông thường, do việc sử dụng HLD sẽ đi kèm với một cấu trúc dữ liệu nào đó và duyệt đồ thị, code có thể sẽ dài và gồm nhiều phần. Tuy nhiên, nếu nắm chắc ý tưởng chính thì cài đặt HLD rất đơn giản.
Tiền xử lý
Đầu tiên, ta cần phải tính kích thước của cây con từng đỉnh để lấy ra các con "nặng" của từng đỉnh một. Ngoài ra, ta cần tính thêm độ sâu các đỉnh để phục vụ cho thao tác tính LCA.
void Dfs(int s, int p = -1) {
Sz[s] = 1;
for(int u: AdjList[s]) {
if(u == p) continue;
Par[u] = s;
Depth[u] = Depth[s] + 1;
Dfs(u, s);
Sz[s] += Sz[u];
}
}Tìm cạnh nặng, cạnh nhẹ và tạo các chuỗi
Sau đó chúng ta thực hiện phân chia các đỉnh vào các chuỗi. Với mỗi đỉnh, cần lưu lại chuỗi của đỉnh và vị trí của đỉnh khi đặt các chuỗi liên tiếp với nhau (để thuận tiện cho việc xử lý truy vấn). Với mỗi chuỗi, chúng ta cần biết đỉnh đầu tiên của chuỗi (để thực hiện việc nhảy giữa các chuỗi).
void Hld(int s, int p = -1) {
if(!ChainHead[CurChain]) {
ChainHead[CurChain] = s;
}
ChainID[s] = CurChain;
Pos[s] = CurPos;
Arr[CurPos] = s;
CurPos++;
int nxt = 0;
for(int u: AdjList[s]) {
if(u != p) {
if(nxt == 0 || Sz[u] > Sz[nxt]) nxt = u;
}
}
if(nxt) Hld(nxt, s);
for(int u: AdjList[s]) {
if(u != p && u != nxt) {
CurChain++;
Hld(u, s);
}
}
}Như vậy, với mỗi đỉnh, chúng ta sẽ tìm cạnh nặng và đi xuống cạnh đó trước. Sau đó, chúng ta sẽ lần lượt tạo ra các chuỗi mới và nhảy sang các đỉnh nhẹ. Như vậy, thứ tự duyệt đồ thị sẽ đảm bảo mỗi chuỗi được lưu đúng thứ tự từ trên xuống dưới trong một đoạn liên tiếp trên mảng $Arr$.
Tìm LCA
Trong phần lớn các bài toán sử dụng HLD để thực hiện truy vấn trên đường đi, chúng ta cần tìm tổ tiên chung gần nhất và thực hiện thao tác lần lượt từ hai đỉnh đến tổ tiên chung này. Rất may là chúng ta có thể sử dụng chính những thông tin đã lưu để tìm ra LCA một cách nhanh chóng.
Khi nhảy từ một node $v$ qua một cạnh nhẹ lên cha của nó, chúng ta luôn nhảy sang một chuỗi có số thứ tự bé hơn (do thứ tự duyệt đồ thị trong hàm $HLD$) nên để tìm LCA của hai đỉnh, chúng ta sẽ tìm chuỗi chứa LCA đó.
Liên tục thực hiện nhảy từ chuỗi có số thứ tự lớn hơn lên một chuỗi có số thứ tự bé hơn (Để đảm bảo không bị nhảy quá, luôn chọn đỉnh đang ở chuỗi có số thứ tự lớn hơn để nhảy) cho đến khi hai đỉnh nằm trên cùng một chuỗi.
Ở đó, đỉnh có độ sâu thấp hơn là LCA của $u$ và $v$.
int LCA(int u, int v) {
while(ChainID[u] != ChainID[v]) {
if(ChainID[u] > ChainID[v]) {
u = Par[ChainHead[ChainID[u]]];
}
else {
v = Par[ChainHead[ChainID[v]]];
}
}
if(Depth[u] < Depth[v]) return u;
return v;
}Segment tree
Duới đây là các thao tác xử lý trên segment tree. Phần này sẽ đủ để xử lý phiên bản không trên cây của bài toán.
int ST[MaxN * 4];
void Build(int id, int l, int r) {
if(l == r) {
ST[id] = Val[Arr[l]];
return;
}
int mid = (l + r) / 2;
Build(id * 2, l, mid);
Build(id * 2 + 1, mid + 1, r);
ST[id] = ST[id * 2] ^ ST[id * 2 + 1];
}
void Upd(int id, int l, int r, int pos, int val) {
if (l > pos || r < pos) return;
if (l == r && l == pos) {
ST[id] = val;
return;
}
int mid = (l + r) / 2;
Upd(id * 2, l, mid, pos, val);
Upd(id * 2 + 1, mid + 1, r, pos, val);
ST[id] = ST[id * 2] ^ ST[id * 2 + 1];
}
int Calc(int id, int tl, int tr, int l, int r) {
if (tl > r || tr < l) return 0;
if (l <= tl && tr <= r) return ST[id];
int mid = (tl + tr) / 2;
return Calc(id * 2, tl, mid, l, r) ^ Calc(id * 2 + 1, mid + 1, tr, l, r);
}Các thao tác trên cây
Và cuối cùng, chúng ta sẽ có các hàm để xử lý truy vấn trên cây. Tất nhiên có thể đưa toàn bộ phần này vào trong main mà không tăng độ dài code. Tuy nhiên để dễ nhìn và tiện debug, chúng ta sẽ code riêng hàm để xử lý truy vấn trên đuờng đi từ đỉnh $u$ đến đỉnh $v$.
void Update(int x, int val) {
Upd(1, 1, N, Pos[x], val);
}
int Query(int u, int v) {
int lca = LCA(u, v);
int ans = 0;
while(ChainID[u] != ChainID[lca]) {
ans ^= Calc(1, 1, N, Pos[ChainHead[ChainID[u]]], Pos[u]);
u = Par[ChainHead[ChainID[u]]];
}
while(ChainID[v] != ChainID[lca]) {
ans ^= Calc(1, 1, N, Pos[ChainHead[ChainID[v]]], Pos[v]);
v = Par[ChainHead[ChainID[v]]];
}
if(Depth[u] < Depth[v]) {
ans ^= Calc(1, 1, N, Pos[u], Pos[v]);
}
else {
ans ^= Calc(1, 1, N, Pos[v], Pos[u]);
}
return ans;
}Do bài toán chỉ yêu cầu cập nhật trên điểm nên hàm $Update$ không có gì đáng chú ý. Độ phức tạp của hàm này là $O(\log(n))$.
Hàm $Query$ dùng để trả lời truy vấn tổng XOR của các số trên đường đi từ $u$ đến $v$. Sau đó, chúng ta thực hiện chia đường đi này thành các đoạn trên các chain rồi thực hiện thao tác tính trên từng đoạn.
Có thể thấy, cách nhảy trong khi tính toán Query chính là cách nhảy khi tìm LCA. Trên thực tế, chúng ta không cần tìm LCA trước mà có thể thực hiện việc đó ngay khi tính Query. Nhưng trong bài này, phần tìm LCA được code riêng một hàm để dễ hiểu và tiện giải thích.
Code đầy đủ
Dưới đây là code đầy đủ cho bài toán (kết hợp của tất cả các đoạn trên, khai báo biến và hàm main) để bạn đọc tham khảo. (Code nộp AC)
Code
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 1e5 + 5;
int N, Q;
int Val[MaxN];
vector<int> AdjList[MaxN]; // input
int Par[MaxN]; // parent
int Depth[MaxN]; // do sau cua node
int Sz[MaxN]; // kich thuoc cua cay con cho cac node
int Pos[MaxN]; // vi tri trong mang cua node
int Arr[MaxN]; // gia tri cua cac phan tu trong mang
int ChainID[MaxN]; // ChainID[i]: Chain ma i nam trong
int ChainHead[MaxN]; // ChainHead[i]: Node dau tien trong chain i
int CurChain, CurPos;
void Dfs(int s, int p = -1) {
Sz[s] = 1;
for(int u: AdjList[s]) {
if(u == p) continue;
Par[u] = s;
Depth[u] = Depth[s] + 1;
Dfs(u, s);
Sz[s] += Sz[u];
}
}
void Hld(int s, int p = -1) {
if(!ChainHead[CurChain]) {
ChainHead[CurChain] = s;
}
ChainID[s] = CurChain;
Pos[s] = CurPos;
Arr[CurPos] = s;
CurPos++;
int nxt = 0;
for(int u: AdjList[s]) {
if(u != p) {
if(nxt == 0 || Sz[u] > Sz[nxt]) nxt = u;
}
}
if(nxt) Hld(nxt, s);
for(int u: AdjList[s]) {
if(u != p && u != nxt) {
CurChain++;
Hld(u, s);
}
}
}
// find LCA
int LCA(int u, int v) {
while(ChainID[u] != ChainID[v]) {
if(ChainID[u] > ChainID[v]) {
u = Par[ChainHead[ChainID[u]]];
}
else {
v = Par[ChainHead[ChainID[v]]];
}
}
if(Depth[u] < Depth[v]) return u;
return v;
}
// Segment Tree
int ST[MaxN * 4];
void Build(int id, int l, int r) {
if(l == r) {
ST[id] = Val[Arr[l]];
return;
}
int mid = (l + r) / 2;
Build(id * 2, l, mid);
Build(id * 2 + 1, mid + 1, r);
ST[id] = ST[id * 2] ^ ST[id * 2 + 1];
}
void Upd(int id, int l, int r, int pos, int val) {
if (l > pos || r < pos) return;
if (l == r && l == pos) {
ST[id] = val;
return;
}
int mid = (l + r) / 2;
Upd(id * 2, l, mid, pos, val);
Upd(id * 2 + 1, mid + 1, r, pos, val);
ST[id] = ST[id * 2] ^ ST[id * 2 + 1];
}
int Calc(int id, int tl, int tr, int l, int r) {
if (tl > r || tr < l) return 0;
if (l <= tl && tr <= r) return ST[id];
int mid = (tl + tr) / 2;
return Calc(id * 2, tl, mid, l, r) ^ Calc(id * 2 + 1, mid + 1, tr, l, r);
}
// Update and queries
void Update(int x, int val) {
Upd(1, 1, N, Pos[x], val);
}
int Query(int u, int v) {
int lca = LCA(u, v);
int ans = 0;
while(ChainID[u] != ChainID[lca]) {
ans ^= Calc(1, 1, N, Pos[ChainHead[ChainID[u]]], Pos[u]);
u = Par[ChainHead[ChainID[u]]];
}
while(ChainID[v] != ChainID[lca]) {
ans ^= Calc(1, 1, N, Pos[ChainHead[ChainID[v]]], Pos[v]);
v = Par[ChainHead[ChainID[v]]];
}
if(Depth[u] < Depth[v]) {
ans ^= Calc(1, 1, N, Pos[u], Pos[v]);
}
else {
ans ^= Calc(1, 1, N, Pos[v], Pos[u]);
}
return ans;
}
// main
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
freopen("cowland.in", "r", stdin);
freopen("cowland.out", "w", stdout);
cin >> N >> Q;
for(int i = 1; i <= N; i++) {
cin >> Val[i];
}
for(int i = 1; i < N; i++) {
int u, v;
cin >> u >> v;
AdjList[u].push_back(v);
AdjList[v].push_back(u);
}
CurPos = CurChain = 1;
Dfs(1);
Hld(1);
Build(1, 1, N);
while(Q--) {
int type;
cin >> type;
if(type == 1) {
// Update
int x, val;
cin >> x >> val;
Update(x, val);
}
else {
int u, v;
cin >> u >> v;
cout << Query(u, v) << '\n';
}
}
}Bài viết tham khảo và bài tập luyện tập
Bài viết trên được tham khảo từ bài viết gốc Hybrid Tutorial 1: Heavy-Light Decomposition. Bạn đọc có thể tham khảo và xem video hướng dẫn kèm theo của galen_colin. Ngoài ra có thể tham khảo bài viết của CP algo.
Trước hết, bạn đọc nên tự cài đặt và nộp bài tập phía trên tại đây. Sau đó có thể làm thêm các bài tập luyện tập dưới đây