Tổng quan về Cấu Trúc Dữ Liệu
Mặc dù máy tính đã có thể xử lý hàng triệu phép tính mỗi giây, nhưng khi một bài toán trở phức tạp, cách tổ chức dữ liệu vẫn vô cùng quan trọng.
Để minh họa điểm này, hãy tham khảo ví dụ sau: bạn đi đến thư viện, thử tìm kiếm một quyển sách với chủ đề nào đó. Các cuốn sách được xếp theo lĩnh vực. Trong mỗi chủ đề, sách lại được xếp theo tên tác giả, nhờ vậy mà việc lấy và cất sách từ giá trở nên khá dễ dàng và đơn giản.
Bây giờ, hãy thử tưởng tượng thay vì tổ chức thành từng giá sách cụ thể, sách được chất thành từng đống ở khắp thư viện. Để tìm được quyển sách của mình, bạn sẽ phải mất hàng giờ, thậm chí rất nhiều ngày.
Tương tự, một phần mềm không thể vận hành hiệu quả khi dữ liệu không được lưu trữ một cách phù hợp với ứng dụng.
Trong bài viết này, chúng ta sẽ cùng nhau điểm qua các loại cấu trúc dữ liệu từ cơ bản đến nâng cao. Để tìm hiểu chi tiết về một cấu trúc dữ liệu, các bạn có thể đọc ở link tương ứng. Trong bài viết này, mình tạm chia các CTDL được chia thành các loại sau:
- CTDL lưu trữ: thường có các thao tác như thêm 1 phần tử, xóa 1 phần tử. Có thể có thêm các thao tác như tìm kiếm 1 phần tử.
- CTDL truy vấn: thường dùng cho các bài toán mà bạn phải duy trì một tập hợp các số và thực hiện 1 số truy vấn trên đó.
- CTDL xâu: dùng cho các bài tập Xử lý xâu.
1. CTDL Lưu trữ
1.1. Mảng (array), danh sách liên kết (linked list)
Mảng và danh sách liên kết là 2 cấu trúc dữ liệu nền tảng cho tất cả các loại cấu trúc dữ liệu khác. Mảng và danh sách liên kết đều được dùng khi bạn muốn lưu nhiều dữ liệu (thường có cùng kiểu dữ liệu). Bảng dưới đây so sánh các thao tác về mảng và danh sách liên kết:
| Mảng | Danh sách liên kết | |
|---|---|---|
| Bộ nhớ | Cố định (cần biết trước số phần tử) | Có thể tăng giảm tùy ý |
| Thêm/Xóa 1 phần tử | $\mathcal{O}(N)$ | $\mathcal{O}(1)$, giả sử biết con trỏ tới phần tử đó |
| Tìm kiếm 1 phần tử | $\mathcal{O}(N)$ | $\mathcal{O}(N)$ |
| Truy cập phần tử | $\mathcal{O}(1)$ | $\mathcal{O}(N)$ |
| Khác | - Ít bộ nhớ hơn - Cache locality: các phần tử ở vị trí gần nhau trên bộ nhớ máy tính, nên khi truy cập các phần tử liên tiếp sẽ nhanh hơn |
Bạn có thể đọc thêm về mảng và danh sách liên kết ở đây
1.2. Stack, Queue, Deque
1.2.1. Stack
Stack là CTDL cho phép thực hiện các thao tác:
- Thêm 1 phần tử vào cuối CTDL
- Xóa 1 phần tử khỏi cuối CTDL
Cả 2 thao tác trên đều có độ phức tạp $\mathcal{O}(1)$. Chú ý ta chỉ có thể xóa phần tử ở cuối CTDL, nói cách khác là phần tử mà mới được thêm vào gần nhất. Vì vậy, Stack còn được gọi là FIFO (First In First Out).
Stack có cài đặt đơn giản và được sử dụng trong nhiều thuật toán như DFS, tìm chu trình Euler, tìm khớp của đồ thị.
Trong C++ STL, có sẵn kiểu dữ liệu stack.
1.2.2. Queue
Queue là CTDL cho phép thực hiện các thao tác:
- Thêm 1 phần tử vào cuối CTDL
- Xóa 1 phần tử khỏi đầu CTDL.
Cả 2 thao tác đều có độ phức tạp $\mathcal{O}(1)$. Chú ý ta chỉ có thể xóa phần tử ở đầu CTDL, nói cách khác là phần tử mà đã được thêm vào lâu nhất. Vì vậy, Stack còn được gọi là LIFO (Last In First Out).
Queue có cài đặt đơn giản và được sử dụng trong BFS.
Trong C++ STL, có sẵn kiểu dữ liệu queue.
1.2.3. Deque
Deque (Double Ended Queue), là CTDL tổng quát hơn của Stack và Queue. Nó cho phép:
- Thêm 1 phần tử vào đầu hoặc cuối CTDL.
- Xóa 1 phần tử khỏi đầu hoặc cuối CTDL.
Cả 2 thao tác đều có độ phức tạp $\mathcal{O}(1)$.
Deque được sử dụng trong một số thuật toán như:
- BFS 01
- Tìm Min/Max trên đoạn tịnh tiến.
Trong C++ STL, có sẵn kiểu dữ liệu deque.
1.3. Priority Queue - Heap
Heap là một cấu trúc dữ liệu cho phép thực hiện các thao tác:
- Thêm một phần tử, với độ phức tạp $\mathcal{O}(\log{N})$.
- Xóa một phần tử, với độ phức tạp $\mathcal{O}(\log{N})$.
- Tìm $max$ của các phần tử, với độ phức tạp $\mathcal{O}(1)$.
Bạn có thể đọc thêm về Heap ở đây
Fibonacci Heap là một dạng heap có độ phức tạp bé hơn. Trong C++, CTDL priority_queue được cài đặt bằng Fibonacci Heap.
1.4. Cây Tìm Kiếm Nhị Phân
Cây Tìm Kiếm Nhị Phân (BST Binary Search Tree) là một cây nhị phân có tính chất: Với mỗi giá trị trên đỉnh đang xét, giá trị của mọi đỉnh trên cây con trái luôn nhỏ hơn đỉnh đang xét và giá trị của mọi đỉnh trên cây con phải luôn lớn hơn đỉnh đang xét.
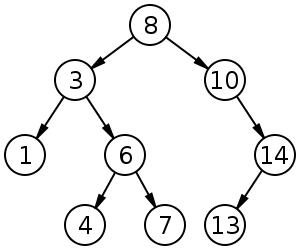
Cây tìm kiếm nhị phân cho phép thực hiện các thao tác:
- Thêm 1 phần tử.
- Xóa 1 phần tử.
- Kiểm tra 1 phần tử có tồn tại hay không.
- Tìm phần tử đầu tiên lớn hơn hoặc bằng 1 giá trị $x$ cho trước.
Trong trường hợp dữ liệu ngẫu nhiên, các thao tác trên có độ phức tạp trung bình là $\mathcal{O}(\log{N})$. Tuy nhiên trong trường hợp xấu nhất, cây tìm kiếm nhị phân bị suy biến (thành 1 "đường thẳng"), thì độ phức tạp mỗi thao tác là $\mathcal{O}(N)$.
Để khắc phục điều này, có rất nhiều CTDL cải tiến từ cây tìm kiếm nhị phân, thường được gọi là các cây nhị phân cân bằng. Khi đó, các thao tác trên có thể được thực hiện với độ phức tạp $\mathcal{O}(\log{N})$. Ví dụ:
-
Cây Đỏ Đen (Red-Black Tree) là một dạng cây tìm kiếm nhị phân (BST) mà sau mỗi truy vấn được thực hiện, cây tự cân bằng theo đúng tính chất của nó với độ phức tạp $O(log(N))$. CTDL set trong C++ được cài đặt bằng cây đỏ đen.
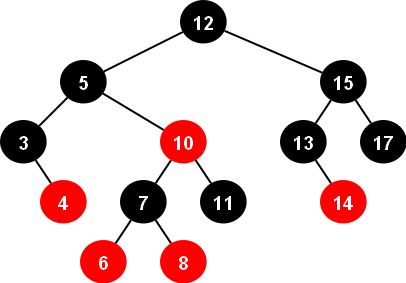
- Splay tree, Skip list, Treap thường được dùng trong các kỳ thi bởi cài đặt đơn giản.
1.5. Bảng băm (Hash Tables)
Bảng băm là một CTDL thường được sử dụng như một từ điển: mỗi phần tử trong bảng băm là một cặp (khóa, giá trị). Nếu so sánh với mảng, khóa được xem như chỉ số của mảng, còn giá trị giống như giá trị mà ta lưu tại chỉ số tương ứng. Bảng băm không như các loại từ điển thông thường - ta có thể tìm được giá trị thông qua khóa của nó.
Bảng băm hoạt động dựa trên hàm Hash: Hash là quá trình khởi tạo một giá trị khóa (thường là 32 bit hoặc 64 bit) từ một phần dữ liệu. Nó có thể là $n$ bit đầu tiên của dữ liệu, $n$ bit cuối cùng, giá trị mod cho một số nguyên tố nào đó. Dựa theo giá trị hash, dữ liệu được chia vào các bucket:
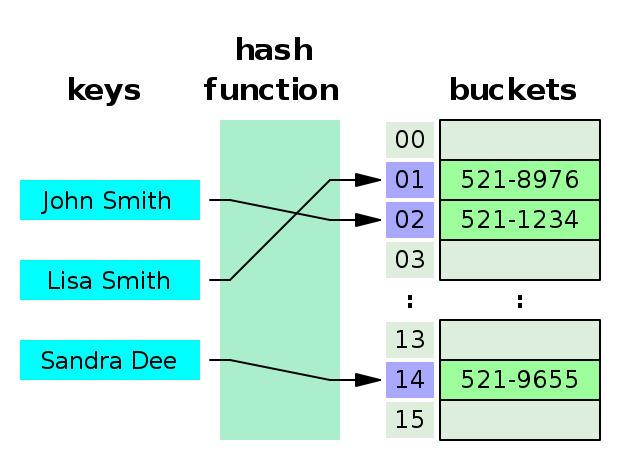
Trong trường hợp hàm Hash hoạt động tốt, mỗi bucket có rất ít phần tử, độ phức tạp của các thao tác trên Hash table như sau:
- Tìm 1 khóa: $\mathcal{O}(1)$.
- Thêm / xóa 1 khóa: $\mathcal{O}(1)$.
Bạn có thể đọc thêm về Hash table ở đây
2. CTDL Truy vấn
2.1. Mảng cộng dồn (Prefix Sum)
Mảng cộng dồn là một cách áp dụng khéo léo mảng. Có 2 dạng bài cơ bản có thể giải được bằng cách áp dụng Prefix Sum.
2.1.1. Mảng cộng dồn - Tìm tổng một đoạn liên tiếp
Ví dụ
- Cho một mảng $a_1,a_2,a_3,…,a_N$.
- Cần trả lời nhiều truy vấn, mỗi truy vấn cho 2 số $L$ và $R$, yêu cầu in ra tổng $a_L + a_{L+1} + … + a_R$.
Cách làm
- Tạo một mảng $S$, với $S_i = a_1 + a_2 + … + a_i$. Mảng $S$ được gọi là mảng cộng dồn
- Với mỗi truy vấn, in ra: $S_R – S_{L-1}$.
2.1.2. Mảng cộng dồn - Tăng giá trị các đoạn
Ví dụ
- Cho mảng $a_1,a_2,…,a_N$.
- Cần thực hiện nhiều truy vấn, mỗi truy vấn cho 3 số $L$, $R$, $V$. Yêu cầu: với mỗi $i (L \le i \le R)$, cộng $V$ vào $a_i$.
- Tính mảng $a$ sau khi thực hiện tất cả các truy vấn.
Cách làm
- Tạo một mảng $P$: $p_1,p_2,…,p_N$
- Khởi tạo $p_i = 0$.
- Với mỗi truy vấn, tăng $p_L$ lên $V$ và trừ $p_{R+1}$ đi $V$.
- Cuối cùng, với mỗi $i$ (từ 1), $p_i += p_{i–1}$. Ta có $a_i = a_i + p_i$.
2.1.3. Mảng cộng dồn trên bảng 2 chiều
Trên bảng 2 chiều $A(i, j)$, ta đặt $f(i, j)$ là tổng các ô trong hình chữ nhật có 2 đỉnh đối diện là $(1, 1)$ và $(i, j)$.
Khi đó, ta có: $f(i, j) = f(i-1, j) + f(i, j-1) - f(i-1, j-1) + A(i, j)$.
Giải thích công thức trên:
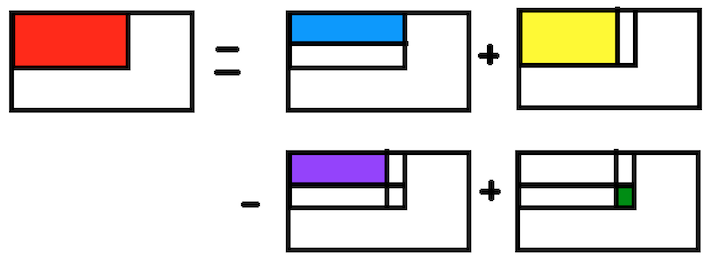
đỏ = xanh da trời + vàng - tím + xanh lá
$f(i, j) = f(i-1, j) + f(i, j-1) - f(i-1, j-1) + A(i, j)$
2.2. Disjoint Sets
Disjoint Sets là cấu trúc dữ liệu được sử dụng trong thuật toán Kruskal và thuật toán Prim - 2 thuật toán tìm cây khung nhỏ nhất của đồ thị. Như tên gọi của nó, Disjoint Set được dùng để quản lý các tập hợp không giao nhau.
Bài toán
Cho đồ thị có $N$ đỉnh. Ta cần thực hiện 2 loại truy vấn:
- Nối 2 đỉnh $i$ và $j$
- Kiểm tra 2 đỉnh $i$ và $j$ có thuộc cùng thành phần liên thông hay không.
Disjoint set cho phép ta thực hiện 2 thao tác trên với độ phức tạp $\mathcal{O}(\log{N})$.
Bạn có thể đọc thêm về Disjoint Set ở bài viết này.
2.3. Sparse Table
Sparse Table là cấu trúc dữ liệu được sử dụng trong bài toán LCA & RMQ.
Với cả 2 bài toán, Sparse Table cho phép:
- Khởi tạo với độ phức tạp: $\mathcal{O}(N* \log{N})$.
- Trả lời truy vấn với độ phức tạp $\mathcal{O}(1)$.
2.4. Segment Tree
Segment Tree, còn được gọi là Interval Tree trong nhiều tài liệu tiếng Việt, là cấu trúc dữ liệu cho phép thực hiện các truy vấn trên một dãy số. Segment Tree rất linh động và có thể áp dụng với nhiều loại truy vấn khác nhau, nên nó xuất hiện rất nhiều trong các kỳ thi.
Với dãy số độ dài $N$, Segment Tree cho phép thực hiện các thao tác với độ phức tạp $\mathcal{O}(\log{N})$.
Bạn có thể đọc thêm về Segment Tree ở đây.
Segment Tree cũng có một mở rộng với nhiều ứng dụng quan trọng là Segment Tree trên tập đoạn thẳng.
2.5. Fenwick
Cũng giống như Segment Tree, Fenwick tree (còn được gọi là Binary Indexed Tree) là cấu trúc dữ liệu cho phép thực hiện các truy vấn trên một dãy số:
- Ưu điểm:
- Độ phức tạp mỗi thao tác cũng là $\mathcal{O}(\log{N})$.
- Hằng số tự nhiên thấp hơn Segment Tree, nên chạy nhanh hơn.
- Dùng ít bộ nhớ hơn.
- Dễ cài đặt hơn Segment Tree
- Nhược điểm:
- Không tổng quát bằng Segment Tree. Tất cả những bài giải được bằng Fenwick tree đều có thể giải được bằng Segment Tree. Nhưng chiều ngược lại không đúng.
Bạn có thể đọc thêm về Fenwick Tree ở đây.
2.6. Heavy-light decomposition
Heavy Light Decomposition là một thuật toán được áp dụng nhiều trong những bài cần xử lý các truy vấn trên cây. Heavy-light decomposition là kĩ thuật phân tách một cây thành nhiều chuỗi đỉnh (chain) rời nhau. Sau đó, chúng ta có thể áp dụng các cấu trúc dữ liệu như Interval Tree hay Binary-Indexed Tree lên những chuỗi này để có thể cập nhật dữ liệu hoặc trả lời các truy vấn trên một đường đi giữa 2 đỉnh trong cây.
Bạn có thể đọc thêm ở: Thuật toán phân tách cây
2.7. Persistent Data Structures
Persistent Data Structures là những cấu trúc dữ liệu được dùng khi chúng ta cần có toàn bộ lịch sử của các thay đổi trên 1 cấu trúc dữ liệu.
Bạn có thể đọc thêm ở: Persistent Data Structures
3. CTDL xâu
3.1. Cây Tiền Tố (Trie)
Trie là một cấu trúc dữ liệu dùng để quản lý một tập hợp các xâu. Trie cho phép:
- Thêm một xâu vào tập hợp, với độ phức tạp $\mathcal{O}(L)$ với $L$ là độ dài xâu cần thêm.
- Xóa một xâu khỏi tập hợp, với độ phức tạp $\mathcal{O}(L)$.
- Kiểm tra một xâu có tồn tại trong tập hợp hay không, với độ phức tạp $\mathcal{O}(L)$.
Ngoài ra trên thực tế, trie cũng rất tiết kiệm bộ nhớ khi áp dụng để lưu các từ có nghĩa, vì vậy nó là một CTDL có ứng dụng rất lớn.
Bạn có thể đọc thêm bài viết về trie.
3.2. Aho Corasick
Bài viết sẽ được cập nhật sau
3.3. Mảng Hậu Tố (Suffix Array)
Suffix Array là một CTDL giúp sắp xếp các hậu tố của một xâu theo thứ tự từ điển. CTDL này thường được sử dụng trong các bài toán xử lý xâu.
Bạn có thể đọc thêm về Suffix Array ở đây.
3.4. Suffix Automaton
Bài viết sẽ được cập nhật sau.
3.5. Palindrome Tree
Palindrome tree (còn được gọi là Eertree), là một CTDL mới được phổ biến vào năm 2014 nhờ bài thuyết trình của Mikhail Rubinchik.
Như tên gọi của nó, Palindrome tree là một CTDL giúp giải quyết các bài toán về Palindrome. Bạn có thể đọc thêm ở đây